In this article was presented solving the equations of Nave — Stocks with the help of actually packs activity. Discussed the analyses of speed epicures.
Ключевые слова: MathCAD, численные методы, Навье-Стокс, движения, скорость.
В последние время появились многие пакетные программы, с помощью появились возможность решения математических задач (в том числе и других задач науки, описывающее такими же математическими моделями) без составления компьютерных программ. В учебном процессе (иногда и в научных учреждениях) с помощью использованием таких систем как MathCAD, Maple, Mat lab, Mathematic и. т.д занятия становятся интереснее, осмысление содержания занятия более быстрое и глубокое а также на укрепление излагаемых понятий и на решение задач остаётся достаточно много времени. Из выше указанных систем, MathCAD — более проще чем остальные и она предназначено для технических вузов, а остальные, можно сказать, для профессиональных математиков. Именно в MathCAD задача формулируется в наиболее естественном математическом виде, а в других математических системах шаги алгоритма решения задачи записываются с помощью команд системы.
В численных методах, ориентированных на задачи гидрогазодинамики, к настоящему времени определился ряд направлений. Среди них выделяются методы конечных разностей, крупных частиц, конечных элементов, интегральных соотношений, сеточно-вариационные и другие. Что касается задач динамики вязкой жидкости, то здесь наибольшие успехи связаны с применением метода конечных разностей. Этот метод выделяется простотой и своей универсальностью и может обеспечить высокую точность результатов.
Перейдем теперь от общих вопросов к выяснению численного решения уравнений Навье — Стокса несжимаемой жидкости. Поскольку эти уравнения содержат оператор Лапласа от проекций скорости, то сами уравнения относятся к эллиптическому или параболическому типам, соответственно для стационарных или нестационарных задач.
Движения несжимаемой жидкости с очень малыми скоростями или в тонких капиллярах, или, наконец, при движении очень вязких жидкостей является так называемое ламинарное (слоистое), при котором линии тока прямые линии, параллельные оси трубы.
Направим ось по оси трубы и будем предполагать трубу бесконечно длинной, а поток — направленным вдоль оси трубы, так что из трех компонент скорости u, v, w остается лишь одна w, а остальные две равны нулю. Отвлекаясь от действия объемных сил и считая поток изотермическим, а следовательно, плотность 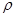 и коэффициент вязкости
и коэффициент вязкости 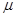 постоянными, будем иметь, согласно уравнениям Навье -Стокса [1], систему уравнений:
постоянными, будем иметь, согласно уравнениям Навье -Стокса [1], систему уравнений:
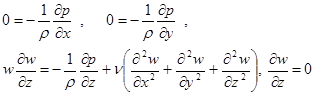 (1)
(1)
Из последнего уравнения этой системы следует, что w представляет собой функцию только x и y, а из первых двух- что p- функция только z. Иными словами, если провести нормальные к оси трубы сечения, то во всех таких сечениях распределения скоростей одинаковы, а давление меняется только от сечения к сечению, сохраняя в данном сечении одинаковое значение. Такие движения называют установившимися.
Предыдущая система равенств сводится к одному
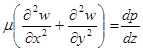 (2)
(2)
Уравнение (2) сводится к линейному уравнению в частных производных второго порядка в плоскости (уравнению Пуассона)
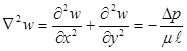 (3)
(3)
Рассмотрим задачу о протекании несжимаемой вязкой жидкости сквозь трубу прямоугольного сечения. Обозначим высоту прямоугольника, параллельную оси Oy, через 2h, а основание, параллельное оси Ox, 2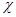 h, где —
h, где — 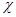 любая положительная постоянная. Ось Oz проведем через центр прямоугольника и направим вниз по потоку, для удобства выбираем безразмерное уравнения и граничные условия [1]:
любая положительная постоянная. Ось Oz проведем через центр прямоугольника и направим вниз по потоку, для удобства выбираем безразмерное уравнения и граничные условия [1]:
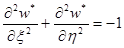 (4)
(4)
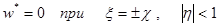 и при
и при 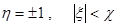 . (
. (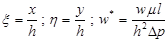 ) (5)
) (5)
Известно что, таких как уравнения (4) в теории разностных схем принято кратко и обобщенно записывать математическую формулировку дифференциальной задачи, включая граничное условия, в виде:
L*w*=f (6)
где L-дифференциальный оператор, w* и f -соответственно искомая функция непрерывного аргумента и заданная правая часть.
Аналогично, разностная задача, поставленная в соответствие дифференциальной (аппроксимирующая последнюю), может быть записана в виде
Lh*w*(h)=f (h) (7)
где Lh — разностный оператор, w*(h) — сеточная функция, f (h)- заданная правая часть, h-шаг сетки [1].
В MathCAD идея решения дискретной задачи Lh*w*(h)=f (h) очень проста и естественна:
w*(h)= 1/Lh*f (h).
Как известно в MathCAD задачи решаются следующими способами [2]:
- с помощью внутренних функций MathCAD;
- с помощью математического алгоритма решения задачи;
- с помощью алгоритма решения задачи, реализованного, во внутренним языке MathCAD.
Для численного решения уравнения (4) в областей 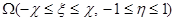 вводим конечно-разностную схему следующим образом. Построим сетки
вводим конечно-разностную схему следующим образом. Построим сетки 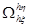 , для этого в области
, для этого в области 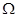 - проводим параллельные прямые на оси координат
- проводим параллельные прямые на оси координат 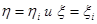 , где
, где 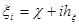 ,
, 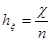 ,
,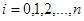
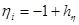 ,
, 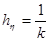 ,
, 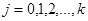 (n, k- число узловые точки). Для построения конечно — разностного уравнения, частные производные заменим следующим образом:
(n, k- число узловые точки). Для построения конечно — разностного уравнения, частные производные заменим следующим образом:
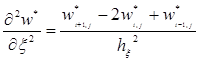
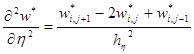
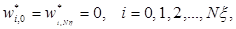
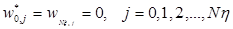

Подставляя их уравнению (4) получим следующее алгебраическое уравнение:
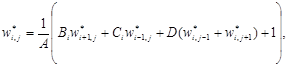 (8)
(8)
где 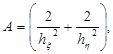
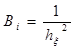 ,
, 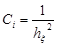 ,
, 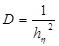
граничные условии:
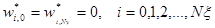
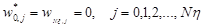
Полученное уравнение решается методом Зейделя с помощью MathCAD.
Вводим следующее команды в окне MathCAD.

Выведем таблицу значений приближённого решения:
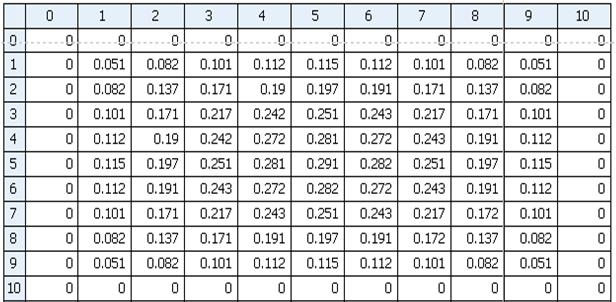
Из полученных результатов можно увидеть, что течение Пуазейловское (максимальное значение скорости в центре) и граничные условия выполняются.
Выведем графики приближённого решения:
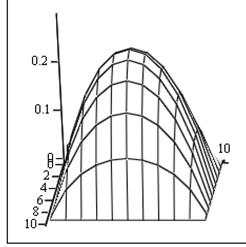
Рис. 1. Эпюра скорости (внешний вид)
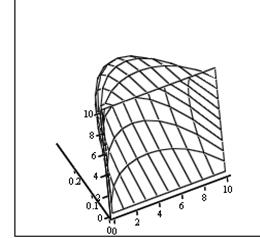
Рис. 2. Эпюра скорости (внутренний вид)
В статье рассмотрен один из методов решения уравнения Навье -Стокса, с помощью MathCAD. Проанализированы эпюры скорости в табличном и графических видах. Видно, что в графическом виде отображение эпюр скорости удобнее и представления свойства течения показательнее. Это происходит благодаря с возможностями программы MathCAD.
Литература:
1. Л. Г. Лойцянский. Механика жидкости и газа. Москва, Наука — 1987г.-840 с.
2. Охарзин.В. А. Прикладная математика в системе Mat CAD. СПб, Лань, 2008г. -352с.







