Рассматривается приложение метода наименьших произведений к параметрической идентификации уравнений короткопериодической составляющей продольного движения.
Ключевые слова:динамические системы, параметрическая идентификация, продольного движение, метод наименьших произведений, приложения.
Метод наименьших квадратов условно можно рассматривать как метод наименьших дисперсий; при этом метод наименьших произведений — методом наименьших спектральных плотностей. Их эквивалентами во временной области являются корреляционные функции. Нетрудно видеть, что метод наименьших квадратов является частным случаем метода наименьших произведений, когда отсчет значений фазовых координат производится в одной и той же точке. Метод представляет значительный интерес в силу большей общности по сравнению с методом наименьших квадратов. Однако до сего времени не имеет широкого распространения.
Недостатки метода наименьших произведений присущи всем известным методам спектральной теории случайных функций.
Рассмотрим приложение метода наименьших произведений к решению задачи параметрической идентификации продольного движения, а именно определению коэффициентов уравнений движения:
,
,
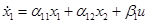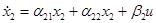где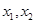 
— фазовые координаты,
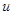- управляющее воздействие.
Откуда
,
.
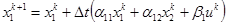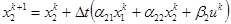Здесь
;
,
.
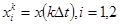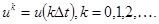
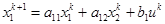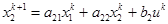Введем
, 
, 
;
, 
, 
.
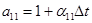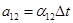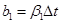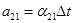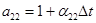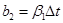По данным нормального функционирования можно получить значения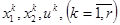 
.
Коэффициенты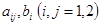 
ищутся из условия минимума 
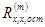(критерии обработки экспериментальных данных; при 
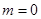получим метод наименьших квадратов):
,
.
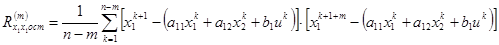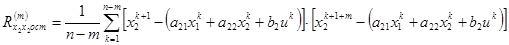Должны иметь
,
,
.
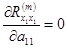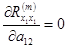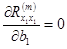Откуда следует:
,
,
.
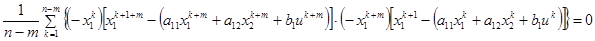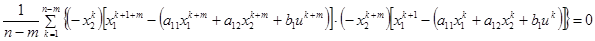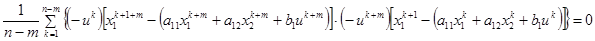Аналогично определятся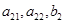 
.
Из первого соотношения получим:
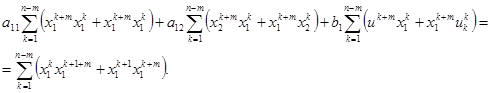
Для эргодических процессов будем иметь:
,
.
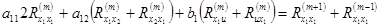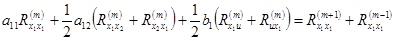Поступая аналогично, получим еще три уравнения.
В итоге получим систему:
,
,
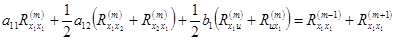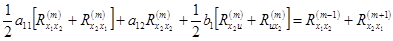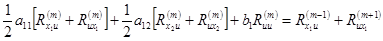. (1)
Для определения 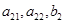получим точно такую же систему, но с правыми частями, соответственно равными
,
,
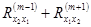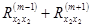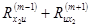. (2)
В общем случае сигналы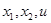 
содержат помехи.
Так что:
,
;
,
.
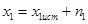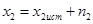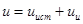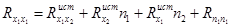При некоррелированных помехах будем иметь:
,
,
.
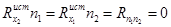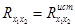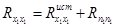Как видим, в составляющих от помех содержатся только автокорреляционные функции, но не содержатся взаимные. Поэтому найдется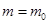 
, такое, что 
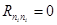, а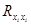 
еще достаточно велико. Поэтому решения систем (1) и (2) при 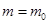дадут состоятельные оценки для коэффициентов 
.
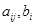Метод широко использовался при разработке тренажных и обучающих комплексов для подготовки операторов и показал свою эффективность [1…7].
Литература:
1. Тюкалов Д. Е., Данилов А. М. Моделирование и подготовка операторов транспортных эргатических систем / Молодой ученый. — 2015. — № 3 (83). — С. 247–249.
2. Гарькина И. А., Данилов А. М., Пылайкин С. А. Имитаторы движения транспортных средств /Альманах современной науки и образования. — 2013. — № 7 (74). — С. 40–42.
3. Гарькина И. А., Данилов А. М., Пылайкин С. А. Практические методы идентификации транспортных эргатических систем / Альманах современной науки и образования. — 2013. — № 8 (75). — С. 50–52.
4. Данилов А. М., Гарькина И. А., Будылина Е. А. Практические методы идентификации эргатической системы / Отраслевые аспекты технических наук. — 2013. — № 6 (30). — С. 03–05.
5. Нугаев А. С., Данилов А. М. Управление в пространстве: оценка зависимостей выходных координат объекта в замкнутой системе / Вестник магистратуры. — 2014. — № 11–1 (38). — С. 27–30.
6. Нугаев А. С., Данилов А. М. Оценка качества объекта управления эргатической системы: функционал качества, определение весовых констант / Вестник магистратуры. — 2014. — № 12–1 (39). — С. 16–19.
7. Будылина Е. А., Гарькина И. А., Данилов А. М. Моделирование с позиций управления в технических системах // Региональная архитектура и строительство. –2013. — № 2. — С. 138–142.
