Производится определение обобщенных характеристик целостной эргатической системы, как некоторой разомкнутой системы (определение передаточных функций человека-оператора и объекта в отдельности практически невозможно в связи с действием организмического принципа). Приводятся методики определения оперативной концептуальной модели, идеальной концептуальной модели, обобщенной частотной характеристики, а также алгоритмы определения необходимых для этого параметров.
Ключевые слова:эргатические системы, эквивалентные характеристики, обобщенная характеристика, методы определения, вычислительные алгоритмы.
В основе приведенной методики лежит использование трендов входных и выходных процессов. Обобщенная характеристика определяется как характеристика некоторой эквивалентной разомкнутой системы со входом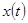 
и выходом 
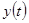(рис.1).
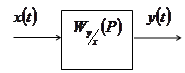
Рис.1
Укажем основные вычислительные алгоритмы, необходимые для определения обобщенной характеристики эргатической системы. Отметим, в связи с действием в эргатических системах организмического принципа, определение параметров оператора и объекта по отдельности принципиально невозможно.
Ограничимся рассмотрением параметров короткопериодической составляющей продольного движения. В качестве 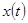примем один из сигналов 
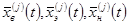. При определении перекрестных связей между каналами пространственного движения в качестве 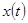принимались и некоторые другие фазовые координаты, их скорости или ускорения. В качестве входных процессов при предварительных исследованиях ограничивались
.
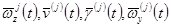Справедливо:
, 
,
,
.
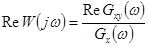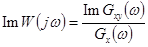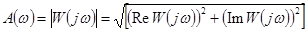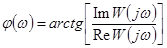Эффективное подавление случайных ошибок при оценивании частотных характеристик переходных процессов (рассматриваются тренды) достигается осреднением по ансамблю оценок, вычисленных по ансамблю независимых реализаций входных и выходных переходных процессов.
При всей кажущейся простоте использованных на практике алгоритмов получение указанных характеристик не столь тривиально. Требуется опыт и инженерная интуиция. Получение результатов, как правило, связано с широким использованием итеративных методов.
Рассмотрим алгоритмы определения основных характеристик, используемых при определении обобщенной характеристики. Прежде всего, введем понятие управляющих воздействий оператора, а именно, под управляющим движением оператора будем понимать:
.
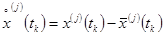Управляющие движения оператора определяются спектральным составом и распределением вероятностей частот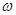 
. Справедливо:
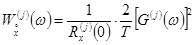
(определяет плотность вероятности [1] случайной величины 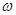в процессе 
:
).
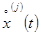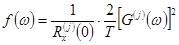Здесь —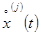 
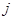-я реализация управляющих движений,
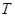— интервал реализации. При этом 
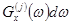представляет собой дисперсию, приходящуюся на участок частот 
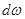, прилежащий к точке (
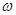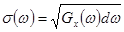определяет среднюю амплитуду гармоник с частотой 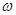в управляющих движениях).
Отметим, что в силу методических и вычислительных погрешностей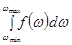 
не будет равняться единице. Поэтому возникает необходимость нормировки, полагая
.
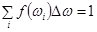Величина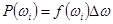 
выражает вероятность попадания в интервал 
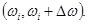Откуда
.
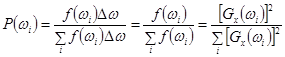Определение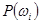 
и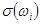 
включает:
- задание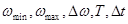 
;
- вычисление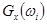 
;
- вычисление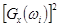 
;
- вычисление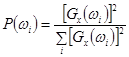 
;
- вычисление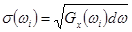 
.
Далее. Концептуальная модель определяется центральной нервной системой. В качестве оперативной концептуальной модели можно принять:
;
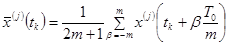в интервале длиной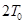 
с центром в точке 
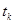математическое ожидание 
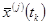приблизительно должны быть линейным (более строго требуется также малость среднего значения корреляционной функции 
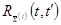в квадрате с центром в точке 
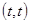и стороной ).
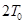Исходя из этого, получим алгоритм определения идеальной концептуальной модели:
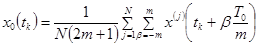
или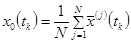 
(усреднение случайной функции 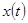как по времени, так и по ансамблю 
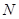реализаций).
Одним из возможных способов определения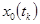 
по нескольким реализациям является одновременное сглаживание всех реализаций. При применении этого способа все реализации случайной функции строятся на одном графике (при правильно выбранном масштабе эти реализации образуют отчетливую полосу). Средняя линия этой полосы (грубо определяется на газ) и даст оценку математического ожидания 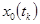. Способ глазомерного сглаживания обладает большой простотой, но является субъективным. Предыдущий метод лишен этого недостатка.
Предложенные алгоритмы прошли многостороннюю апробацию при разработке тренажеров для подготовки операторов эргатических систем различного назначения [2…8].
Литература:
1. Данилов А. М., Гарькина И. А. Теория вероятностей и математическая статистика с инженерными приложениями: учебное пособие. — Пенза: ПГУАС. — 2010. — 228 с.
2. Данилов А. М., Лапшин Э. В., Гарькина И. А., Трусов В. А. Информационно-вычислительные системы авиационных тренажеров модульной архитектуры с распараллеливанием вычислительных процессов / Инновации на основе информационных и коммуникационных технологий. — 2010. — № 1. — С. 379–383.
3. Еремкин А. И., Прошин А. П., Данилов А. М., Гарькина И. А. Системные проблемы и моделирование при разработке сложных систем / Надежность. — 2006. — № 1. — С. 3.
4. Петренко В. О., Данилов А. М. Управление в пространстве: идентификация управляющих воздействий / Современные научные исследования и инновации. — 2014. — № 12–1 (44). — С. 146–149.
5. Антонова Е. А., Будылина Е. А., Гарькина И. А. Автономные исследования сепаратных подсистем при синтезе структурированных систем / Новый университет. Серия: Технические науки. — 2014. — № 2 (24). — С. 38–40.
6. Сухов Я. И., Гарькина И. А. Определение характеристик эргатической системы по данным нормального функционирования / Современные научные исследования и инновации. — 2014. — № 11–1 (43). — С. 107–111.
7. Гарькина И. А., Таишева А. Р.Влияние коэффициента усиления на области равных оценок оператором технических характеристик объекта / Гарькина И. А., Таишева А. Р. Вестник магистратуры. — 2014. — № 4–1 (31). — С. 28–31.
8. Хнаев О. А., Гарькина И. А. Приближение многомерных функций обобщенными многочленами / Вестник магистратуры. — 2014. — № 2 (29). — С. 41–44.
