Работа посвящена разработке кинематической модели космического манипуляционного робота, функционирующего вблизи космической станции. Рассматриваемая механическая система представляется как свободнолетающая платформа с установленным на ней трехзвенным манипулятором. Приводится решение первой задачи кинематики манипулятора с использованием пакета расширения Symbolic Math Toolbox математического пакета Matlab.
Ключевые слова: космическая робототехника, кинематическая модель, первая задача кинематики манипулятора.
Введение. Космический манипуляционный робот, предназначенный для обслуживания орбитальной космической станции, рассматривается как свободнолетающая платформа с установленными на ней манипуляторами или манипулятором (Рис. 1) [1]. Необходимость изучения и создания такого класса объектов определяется широким спектром задач, которые могут быть решены с его помощью [2–5].
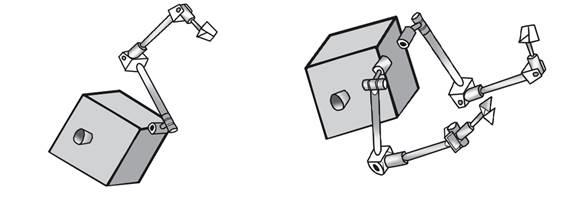
Рис. 1. Схематичные изображения космических манипуляционных роботов
В задачи исследования космических роботов обычно входит [6]:
- Построение кинематической схемы рассматриваемой механической системы и определение обобщенных координат робота.
- Разработка кинематической модели, которая включает в себя описание пространственного положения робота через обобщенные координаты, а также определение угловых и линейных скоростей робота по заданному вектору обобщенных скоростей.
Основные методы исследования космических роботов представлены в работах [1–5, 8–11].
Кинематическая схема.
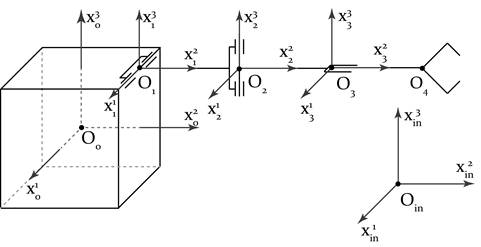
Рис. 2. Кинематическая схема космического манипуляционного робота
На рис. 2 представлена кинематическая схема данной механической системы, состоящей из четырех тел: основания и трех звеньев. Звенья соединены с помощью цилиндрических шарниров, которые обеспечивают вращательные движения звена вокруг оси шарнира. С каждым телом связана соответствующая система координат. Нижний индекс в обозначениях систем координат отвечает за принадлежность системы к определенному телу робота. Робот движется в инерциальной системе координат, которую мы связываем с орбитальной космической станцией.
Обобщенные координаты рассматриваемого космического манипуляционного робота представлены на рис. 3.
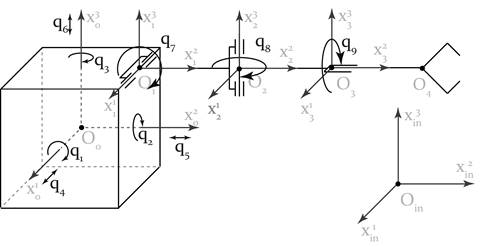
Рис. 3. Обобщенные координаты космического манипуляционного робота
Здесь 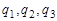 — углы поворота системы координат связанной с корпусом относительно соответствующих осей инерциальной системы,
— углы поворота системы координат связанной с корпусом относительно соответствующих осей инерциальной системы, 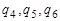 — координаты центра масс корпуса в инерциальной системе,
— координаты центра масс корпуса в инерциальной системе, 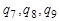 — углы поворота звеньев относительно системы координат предыдущего тела.
— углы поворота звеньев относительно системы координат предыдущего тела.
Кинематическая модель. Одной из главных задач кинематики манипуляторов является определение положения полюсов робота и характеристической точки инструмента в инерциальной системе координат через обобщенные координаты. Полюсами робота в нашем случае будут точки 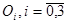 , изображенные на рис. 2, точка
, изображенные на рис. 2, точка 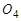 — характеристическая, она определяет положение инструмента манипулятора. Таким образом, задача состоит в следующем: для заданной кинематической схемы космического манипуляционного робота по известному вектору обобщенных координат и заданным геометрическим параметрам звеньев и основания робота определить положение полюсов робота и его характеристической точки относительно абсолютной системы координат. В дальнейшем под
— характеристическая, она определяет положение инструмента манипулятора. Таким образом, задача состоит в следующем: для заданной кинематической схемы космического манипуляционного робота по известному вектору обобщенных координат и заданным геометрическим параметрам звеньев и основания робота определить положение полюсов робота и его характеристической точки относительно абсолютной системы координат. В дальнейшем под 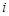 -ой точкой будем подразумевать точку
-ой точкой будем подразумевать точку 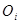 .
.
Для определения положения 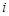 -ой точки в абсолютной системе координат нам необходимо найти ее положение в системе координат
-ой точки в абсолютной системе координат нам необходимо найти ее положение в системе координат 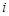 -го тела, а также в системах координат, связанных с предыдущими телами. В таком случае положение
-го тела, а также в системах координат, связанных с предыдущими телами. В таком случае положение 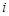 -ой точки в абсолютном пространстве будет определятся следующим образом [6]:
-ой точки в абсолютном пространстве будет определятся следующим образом [6]:
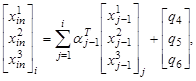
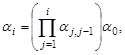
где 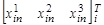 –вектор-столбец описывающий положение
–вектор-столбец описывающий положение 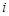 -ой точки в инерциальной системе координат,
-ой точки в инерциальной системе координат, 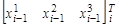 –вектор-столбец описывающий положение
–вектор-столбец описывающий положение 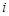 -ой точки в системе координат
-ой точки в системе координат 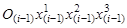 ,
,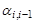 – матрицы поворота системы координат
– матрицы поворота системы координат 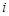 -го тела относительно
-го тела относительно 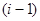 -го, которые выглядят таким образом (в предположении, что
-го, которые выглядят таким образом (в предположении, что 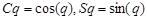 ):
):
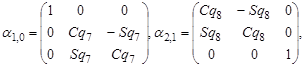
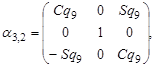
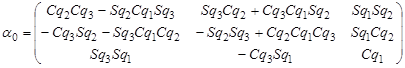 .
.
Теперь получим уравнения связи векторов угловых и линейных скоростей робота с вектором обобщенных скоростей. Для вывода уравнений связи воспользуемся теоремой о сложении угловых скоростей, а также теоремой о сложении скоростей в сложном движении [7].
В таком случае уравнения связи векторов угловых и линейных скоростей робота с вектором обобщенных скоростей будут выглядеть следующим образом:
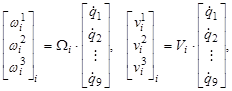
Здесь 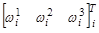 — вектор угловой скорости
— вектор угловой скорости 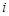 -го тела в
-го тела в 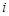 -ой системе координат,
-ой системе координат, 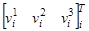 – вектор линейной скорости
– вектор линейной скорости 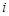 -ой точки в системе координат связанной с
-ой точки в системе координат связанной с 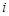 -ым телом,
-ым телом, 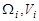 — матрицы связи угловых и линейных скоростей робота с вектором обобщенных скоростей, которые представлены в виде:
— матрицы связи угловых и линейных скоростей робота с вектором обобщенных скоростей, которые представлены в виде:
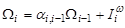 ,
,
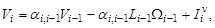
где матрица 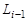 характеризует конструктивные параметры
характеризует конструктивные параметры 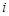 -го тела и выглядят таким образом:
-го тела и выглядят таким образом:
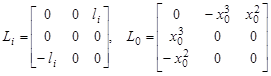 ,
,
здесь 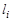 — длина
— длина 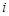 -го звена,
-го звена, 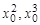 — координаты точки
— координаты точки 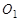 в системе координат основания.
в системе координат основания.
Матрица 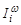 размерности
размерности 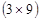 имеет единственный единичный элемент стоящий на пересечении
имеет единственный единичный элемент стоящий на пересечении 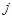 -ой строки и
-ой строки и 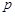 -го столбца,
-го столбца, 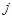 принимает значения 1,2 или 3 при совпадении оси шарнира с соответствующей координатной осью
принимает значения 1,2 или 3 при совпадении оси шарнира с соответствующей координатной осью 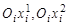 или
или 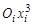 ,
, 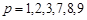 и зависит от номера рассматриваемой обобщенной координаты, остальные элементы равны нулю. Аналогично определяется матрица
и зависит от номера рассматриваемой обобщенной координаты, остальные элементы равны нулю. Аналогично определяется матрица 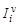 , но
, но 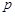 здесь принимает значения 4, 5 и 6. Матрицы
здесь принимает значения 4, 5 и 6. Матрицы 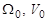 определяются следующим образом:
определяются следующим образом:
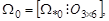
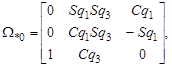
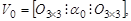
Пример.
Представим решение первой задачи динамики для конкретной кинематической схемы космического манипуляционного робота по заданным законам изменения обобщенных координат. Моделирование осуществлялось с помощью математического пакета Matlab.
Пусть обобщённые координаты изменяются по такому закону:
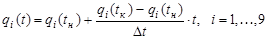 ,
,
где 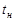 — начальный момент времени,
— начальный момент времени, 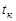 — конечный момент времени,
— конечный момент времени,  — промежуток времени, на котором рассматривается изменение обобщенных координат
— промежуток времени, на котором рассматривается изменение обобщенных координат
При моделировании использовались следующие значения параметров космического манипуляционного робота:
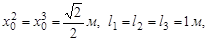
Начальные и конечные значения для обобщенных координат:
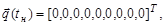
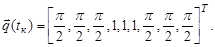
Уравнения движения точек 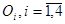 и графики изменения величин обобщенных скоростей строятся на промежутке времени
и графики изменения величин обобщенных скоростей строятся на промежутке времени 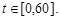
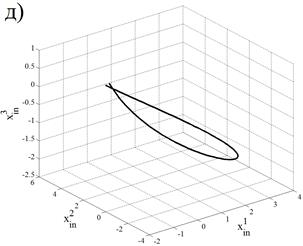
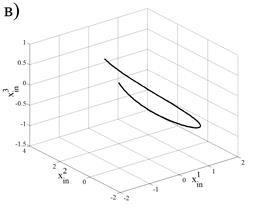
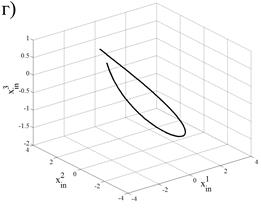
На рис. 4 и рис. 5 представлены траектории движения точек робота в инерциальной системе координат.
|
|
|
||
|
|
|
||
|
Рис. 4. Траектории движения точек робота: (а) — траектория точки |
|||
|
|
|
|
|
|
Рис. 5. (д) — траектория точки |
|||
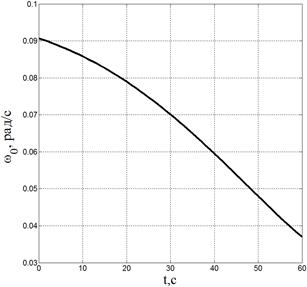
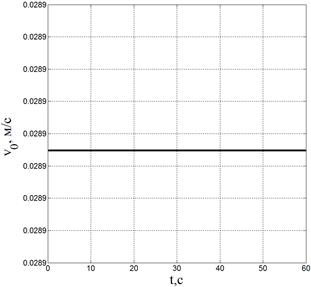
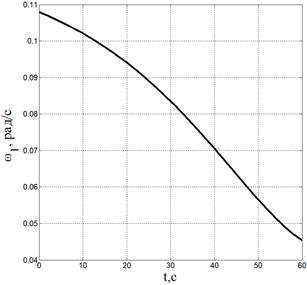
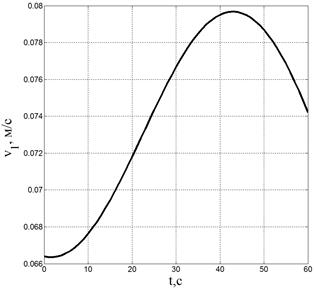
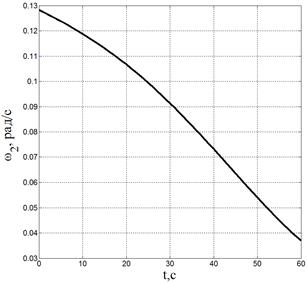
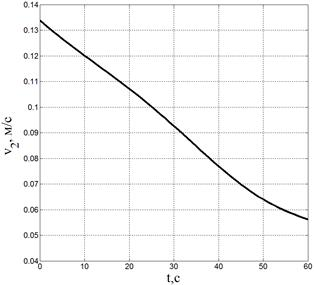
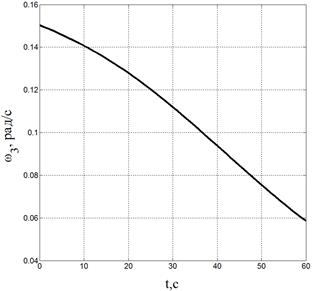
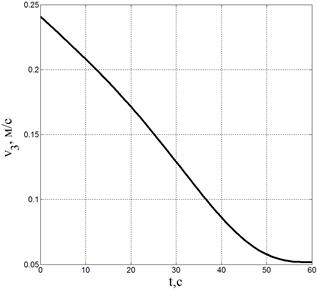
Также приведены графики изменения величин обобщенных скоростей на рис. 6–7.
|
|
|
|
|
|
|
Рис. 6. Изменения величин угловых и линейных скоростей основания и 1-го звена |
|
|
|
|
|
|
|
|
Рис. 7. Изменения величин угловых и линейных скоростей 2-го и 3-го звена |
|
Заключение.
В ходе работы были получены следующие результаты:
- Построена кинематическая схема космического манипуляционного робота и определены его обобщенные координаты.
- Разработана кинематическая модель рассматриваемой механической системы.
- Представлена реализация первой задачи кинематики для заданной модели космического робота в виде графического представления траекторий точек робота в абсолютной системе координат. Также проиллюстрирована зависимость угловых и линейных скоростей робота от времени. Реализация осуществлялась при помощи пакета расширения Symbolic Math Toolbox математического пакета Matlab.
Литература:
1. Глумов В. М., Земляков С. Д., Рутковский В. Ю., Суханов В. М., Оперативный компьютерный вывод и декомпозиция уравнений движения космического модуля // Автомат. и телемех., 2006, № 1, С. 89–116.
2. Кулаков Ф. М., Шмыров А. С., Шиманчук Д. В. Управление космическим роботом с использованием неустойчивой точки либрации // Мехатроника, автоматизация, управление. 2014. № 7. С. 23–28.
3. Кулаков Ф. М., Шмыров А. С., Шиманчук Д. В. Методы управления движением космического робота в окрестности точек либрации // XII Всероссийское совещание по проблемам управления ВСПУ-2014 Институт проблем управления им. В. А. Трапезникова РАН. Москва, Институт проблем управления им. В. А. Трапезникова РАН, 2014. — С. 3792–3801
4. Kulakov F., Shmyrov A., Shymanchuk D. Supervisory Remote Control of Space Robot in an Unstable Libration Point // Proceedings of the 2013 IEEE 7th International Conference on Intelligent Data Acquisition and Advanced Computing Systems, IDAACS 2013, 2013. Vol. 2. P. 925–928
5. Shmyrov A., Shmyrov V., Shymanchuk D. Prospects for the use of space robots in the neighbourhood of the libration points // Applied Mathematical Sciences, 2014. Vol. 8, no. 50.P. 2465–2471
6. Кулаков Ф. М. Супервизорное управление манипуляционными роботами. М. Наука 1980г. 448 с.
7. Бухгольц Н. Н. Основной курс теоретической механики. М.: Наука, 1965. 468 с.
8. Алферов Г. В., Кулаков Ф. М., Нечаев А. И., Чернакова С. Э. Информационные системы виртуальной реальности в мехатронике и робототехнике: Учеб. пособие. — СПб.: Изд-во С.-Петерб. ун-та, 2009. — 168 с.
9. Ефимова П. А., Шиманчук Д. В. Моделирование движения космического манипуляционного робота // Проблемы механики и управления: Нелинейные динамические системы: межвуз. сб. науч. тр. / Перм. гос. нац. иссл. ун-т. — Пермь, 2014. — Вып. 46. — 148 с. С. 20–30.
10. Кулаков Ф. М., Алферов Г. В., Шарлай А. С. Кинематические модели манипуляционных роботов // Потенциал современной науки, № 2, Липецк, С.38–41, апрель, 2014
11. Кулаков Ф. М., Алферов Г. В. Модели манипуляторов для автоматизации сборочных операций. // Современные инновации в науке и технике / Сборник трудов 4-й научно-практической конференции. Курск, 2014. Том 2, С. 322–329.







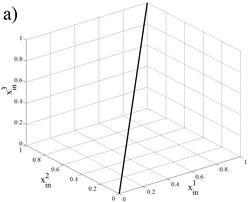
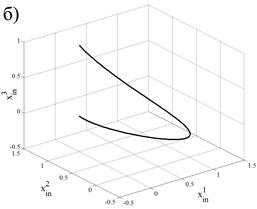
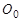 , (б) — траектория точки
, (б) — траектория точки 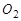 , (г) — траектория точки
, (г) — траектория точки