В статье на нескольких примерах показано, что с помощью метода интерполяции по коэффициенту формы можно достаточно просто определять величину максимального прогиба прямоугольных пластинок со сложными граничными условиями, нагруженных равномерно распределенной нагрузкой. В основе метода интерполяции по коэффициенту формы лежит изопериметрический метод. Основным аргументом в получаемых аналитических зависимостях является отношение коэффициента формы к площади области. Все определенное ограниченное подмножество областей имеют граничные (опорные) решения.
The article in propose a new geometry method for definite maximum bend plate in form different and complicated limit condition with equality distribution load. At the heart of an interpolation method on a form factor the isoperimetric method lays. The basic argument in received analytical dependences is the relation of a form factor to the area. All decisions for a certain restrained subset of areas have boundary (basic) decisions.
Метод интерполяции по коэффициенту формы предложен А. В. Коробко [1], его основу положены изопериметрические свойства и закономерности интегральной характеристики формы плоской области — коэффициента формы Кf. Впервые коэффициент формы был применен Д. Пойа [2] при построении изопериметрических односторонних и двусторонних неравенств для оценки интегральных физических характеристик в некоторых задачах математической физики.
Коэффициент формы плоской области и является количественной характеристикой формы области и выражается через контурный интеграл:
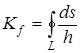, (1)
где ds — линейный элемент контура области (рис. 1,а); h — высота, опущенная из полюса, взятого в нутрии области, на касательную к переменной точке контура; L — периметр области.
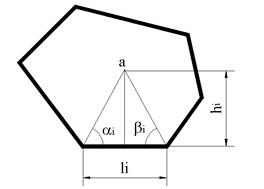
Рис. 1.
Для областей с полигональным контуром (Рис.1) выражение (1) имеет вид:
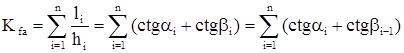, (2)
где li, hi длина i-той стороны многоугольника и высота, опущенная из полюса на i-ю сторону (рис.1);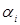 
и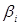 
- углы прилежащие к i-той стороне и ограниченные отрезками прямых, проведенными из полюса в углы полигона;n- количество сторон многоугольника.
Для прямоугольников коэффициент формы определяется по формуле:
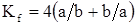. (3)
Более подробные сведения об этой характеристике приведены в работе [1].
Сущность метода интерполяции по коэффициенту формы заключается в следующем. Выбирается геометрическое преобразование заданной пластинки с таким расчетом, чтобы в полученное множество форм пластинок входили хотя бы две, для которых известны решения, либо их можно получить каким-либо точным или приближенным методом. Имея опорные решения, приводим их к изопериметрическому виду:
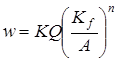, (4)
где n и K — неизвестные параметры.
Эти параметры определяются из известных решений (w0)1 и (w0)2, которые называются опорными решениями, а соответствующие им формы пластинок — опорными фигурами. Используя опорные решения и структуру формул, полученных при преобразовании интегро-дифференциальных соотношений технической теории пластинок:
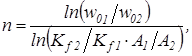(5)
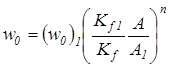. (6)
где индексы 1 и 2 относятся к параметрам двух опорных пластинок. В этих выражениях первые формулы соответствуют опорным пластинкам с различной площадью, а вторые — с равной площадью.
Графически рассмотренная аппроксимация изображена на рисунке 2, где кривая I соответствует действительным значениям wo, а кривая II — приближенным решениям, полученным по формуле (6). Приведенные выше рассуждения основывались на непрерывных геометрических преобразованиях, когда изменение формы фигур рассматриваемого множества происходит непрерывно и монотонно.
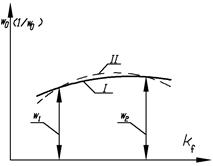
Рис. 2
Таким образом, МИКФ по своей математической сущности является методом интерполяции по коэффициенту формы решений, расположенных между опорными. Применение МИКФ даёт возможность получать простые аналитические зависимости для определения интегральных характеристик в задачах строительной механики, связанных с выпуклой плоской областью. МИКФ также даёт возможность проводить контрольные проверки результатов решений для конкретных фигур, полученных другими приближенными способами, путём построения этих фигур с помощью различных геометрических преобразований.
Рассмотрим прямоугольные пластинки, нагруженные равномерно распределенной нагрузкой, имеющие комбинированные граничные условия.
Пример 1. Рассмотрим пластинку постоянной толщины, комбинированно опертую рис.3, нагруженную равномерно распределенной по всей поверхности нагрузкой. Требуется найти решение и оценить погрешность для прогиба пластинок в виде прямоугольников с соотношением сторон 1,2; 1,4; 1,6; 1,8; 2; 2,2; 2,4; 2,4; 2,6; 2,8.
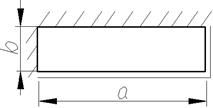
Рис. 3 Условия операния пластинки
Приняв в качестве опорных фигур пластинки в виде прямоугольников с a/b=1 (Кf = 8; 1000W0 = 2,2138) и a/b=3 (Кf = 13,333; 1000W0 = 0,5999) по формулам МИКФ находим максимальный прогиб для заданных пластин, найденные данные сведены в таблицу 1.
Таблица 1
Значения максимального прогиба прямоугольных пластинок с комбинированными граничными условиями
|
Характеристики пластинок |
a/b |
||||||||||
|
1 |
1,2 |
1,4 |
1,6 |
1,8 |
2 |
2,2 |
2,4 |
2,6 |
2,8 |
3 |
|
|
1000W0 (МКЭ) |
2,2138 |
2,1227 |
1,909 |
1,672 |
1,4358 |
1,23 |
1,055 |
0,907 |
0,7856 |
0,684 |
0,5999 |
|
1000W0(МИКФ) |
|
2,1184 |
1,914 |
1,669 |
1,4389 |
1,231 |
1,055 |
0,9087 |
0,786 |
0,6849 |
|
|
Кf |
8 |
8,1333 |
8,4571 |
8,9 |
9,422 |
10 |
10,6182 |
11,267 |
11,938 |
12,628 |
13,333 |
|
Разница, % |
|
0,2 |
0,27 |
0,2 |
0,22 |
0,12 |
0 |
0,19 |
0,06 |
0,14 |
|
Пример 2. Рассмотрим пластинку постоянной толщины, комбинированно опертую рис.4, нагруженную равномерно распределенной по всей поверхности нагрузкой. Требуется найти решение и оценить погрешность для прогиба пластинок в виде прямоугольников с соотношением сторон 1,2; 1,4; 1,6; 1,8; 2; 2,2; 2,4; 2,4; 2,6; 2,8.
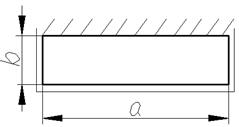
Рис. 4 Условия опирания пластинки
Приняв в качестве опорных фигур пластинки в виде прямоугольников с a/b=1 (Кf = 8; 1000W0 = 2,886) и a/b=3 (Кf = 13,333; 1000W0 = 0,603) по формулам МИКФ находим максимальный прогиб для заданных пластин, найденные данные сведены в таблицу 2.
Таблица 2
Значения максимального прогиба прямоугольных пластинок с комбинированными граничными условиями
|
Характеристики пластинок |
a/b |
||||||||||
|
1 |
1,2 |
1,4 |
1,6 |
1,8 |
2 |
2,2 |
2,4 |
2,6 |
2,8 |
3 |
|
|
1000W0 (МКЭ) |
2,886 |
2,528 |
2,145 |
1,803 |
1,513 |
1,274 |
1,079 |
0,922 |
0,793 |
0,689 |
0,603 |
|
1000W0(МИКФ) |
|
2,642 |
2,1836 |
1,8189 |
1,5213 |
1,2785 |
1,0828 |
0,9232 |
0,7953 |
0,689 |
|
|
Кf |
8 |
8,1333 |
8,4571 |
8,9 |
9,422 |
10 |
10,6182 |
11,267 |
11,938 |
12,628 |
13,333 |
|
Разница, % |
|
4,52 |
1,798 |
0,88 |
0,55 |
0,35 |
0,35 |
0,13 |
0,3 |
0 |
|
Анализируя результаты, представленные в таблицах 1 и 2 можно сделать вывод о том, погрешность решения, полученного с помощью метода интерполяции по коэффициенту формы (строка 2 табл. 1 и 2) и метода конечных элементов (строка 1 табл. 1 и 2) мала и не превышает 5 %.
Таким образом, МИКФ дает возможность достаточно просто и с высокой степенью точности находить значения изгиба в задачах строительной механики пластинок, связанных с прямоугольными областями с комбинированными граничными условиями.
Литература:
1. Коробко А. В. Геометрическое моделирование формы области в двумерных задачах теории упругости. [Текст] / В. И. Коробко — М.: Изд-во АВС, 1999. — 320с.
2. Полиа Г., Сеге Г. Изопериметрические неравенства в математической физике. — М.: Госматиздат, 1962. — 336с.
3. Фетисова М. А., Калашникова Н. Г. Определение максимального прогиба трапециевидных пластинок с комбинированными граничными условиями с помощью МИКФ/ Известия ОрелГТУ. Серия «Строительство. Транспорт». — Орел: изд-во ОрелГТУ, 2009. — № 1. — с.65–67.
4. Коробко А. В., Фетисова М. А. Определение поперечного изгиба методом интерполяции по коэффициенту формы при аффинном преобразовании пластинок в виде ромбов и параллелограммов с комбинированными граничными условиями/ Промышленное и гражданское строительство. Москва, 2010. — № 1. — С.23–24.
5. Коробко А. В., Фетисова М. А. Способы решения задач поперечного изгиба трапециевидных пластинок/ «Строительство. Реконструкция». — Орел: изд-во ОрелГТУ, 2010. — № 1. — С. 36–39.
