Процессы массообмена, происходящие при ректификации углеводородов, связаны с переходом компонентов из одной фазы в другую. Движущей силой этих процессов является разность концентраций или градиент концентраций, а скорость процесса определяется скоростью перехода вещества из одной фазы в другую. Массообменные процессы обратимы, т. е. направление переноса компонентов смеси может изменяться в зависимости от рабочих условий (давления, температуры) и свойств разделяемой смеси. Перенос вещества прекращается при достижении состояния равновесия между фазами.
В результате массообмена концентрация каждого компонента в обеих фазах изменится и, в конце концов, наступит состояние равновесия. Состояние равновесия следует понимать так, что обмен между фазами не прекращается, однако скорости перехода компонентов из одной фазы в другую выравниваются. В состоянии равновесия между концентрациями любого компонента смеси в обеих фазах имеется определенная зависимость. Так, если в фазе L концентрация какого-то компонента х*, а в фазе G — концентрация у*, то в состоянии равновесия [8–11]
y*=f1(x), (1.1)
соответственно
x*=f2(y). (1.2)
Соотношение между фактической концентрацией и равновесной позволяет судить о направлении процесса. Если фактическая концентрация компонента в фазе G больше равновесной (у >> у*), то данный компонент будет переходить из фазы G в фазу L. Если имеет место обратное соотношение, то переход вещества происходит из фазы L в фазу G. В зависимости от процесса и участвующих в нем веществ определяется конкретный вид уравнений (1.1) и (1.2).
Нефть, газовый конденсат и их фракции являются многокомпонентными смесями, состоящими из большого числа компонентов. Поэтому обычно нефть и нефтепродукты рассматривают состоящими из некоторого числа (обычно 10 и более) узких по температурам кипения фракций, отождествляемых с индивидуальными компонентами. В координатах х* — у* каждому такому компоненту (фракции) отвечает своя кривая равновесия.
Согласно закону конвективной диффузии, количество вещества М, переданного в единицу времени из фазы к поверхности раздела фаз, пропорционально поверхности фазового контакта dF и разности концентраций в потоке Сф и на границе раздела фаз Сгр, т. е.
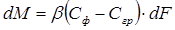, (1.3)
где β — коэффициент массоотдачи.
При ректификации нефтегазоконденсатных смесей скорость переноса вещества из одной фазы в другую dM пропорциональна движущей силе процесса ΔC, характеризующей степень отклонения системы пар — жидкость от состояния равновесия, и поверхности контакта фаз dF. Следовательно
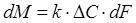, (1.4)
где k — коэффициент массопередачи; ΔС — движущая сила процесса.
Сутью коэффициента массопередачи является характеристика величины массы вещества, переходящего из одной фазы в другую в единицу времени через единицу поверхности контакта фаз при движущей силе процесса, равной единице. Однако независимо от этого ΔС = С*–С, где С — фактическая концентрация в ядре потока одной из фаз, а С* — равновесная концентрация в той же фазе. Из сопоставления уравнений (1.3) и (1.4) нетрудно установить, что размерности коэффициентов массопередачи и массоотдачи одинаковы.
Иногда используют объемный коэффициент массопередачи, относя количество переданной массы к единице объема ректификационной колонны или контактной ее зоны. В этом случае уравнение массопередачи при ректификации можно записать в следующем виде:
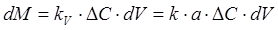, (1.5)
где а — поверхность контакта фаз в единице рабочего объема колонны или ее контактной зоны, м2/м3; KV — объемный коэффициент массопередачи, равный
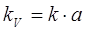. (1.6)
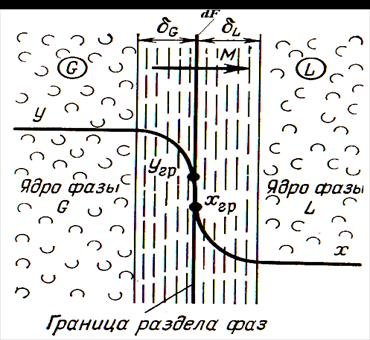
Рис. 1. Схема массообменного процесса при ректификации между жидкой и паровой фазами
В соответствии со схемой, приведенной на рис. 1, процесс массопередачи из фазы L в фазу G можно представить следующими уравнениями массопередачи [1–6; 7–10]:
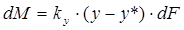, или 
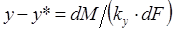, (1.7)
конвективной диффузии со стороны фазы G к границе раздела фаз и от границы раздела в фазу L
, 
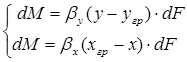или
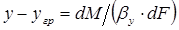, (1.8)
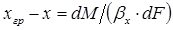. (1.9)
Уравнение равновесия между фазами представим в виде прямой
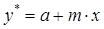, (1.10)
где m — тангенс угла наклона равновесной линии. Поскольку на границе раздела фаз имеет место состояние равновесия, то
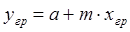. (1.11)
Из уравнений (1.10) и (1.11) получим
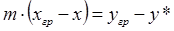. (1.12)
С учетом этого выражения, умножив обе части уравнения (1.9) на т, получим
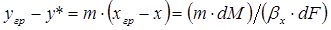. (1.13)
Сложив левые и правые части уравнений (1.8) и (1.13), получим
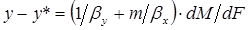. (1.14)
Сопоставив между собой уравнения (1.7) и (1.14), получим следующую зависимость между коэффициентом массопередачи kу и коэффициентами массоотдачи βy и βx:
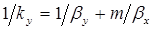. (1.15)
Первое слагаемое 1/βy соответствует сопротивлению массопереносу в фазе G, а второе m/βx — сопротивлению массопереносу в фазе L. Таким образом, полученный результат можно сформулировать так: общее сопротивление массопереносу между фазами равно сумме фазовых сопротивлений массопереносу.
Если обе части уравнения (1.15) разделить на т, то нетрудно установить, что
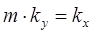, (1.16)
где kх — коэффициент массопередачи при представлении движущей силы через концентрации компонента в жидкой фазе L.
С учетом этого получим также другую запись закона аддитивности фазовых сопротивлений массопереносу
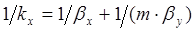. (1.17)
Коэффициент массоотдачи представляет собой массу вещества, переданную через единицу поверхности в единицу времени при разности концентраций в ядре потока и на границе раздела фаз, равной единице. Коэффициент массоотдачи определяется гидродинамическими и физико-химическими факторами, а также геометрией и размерами системы. Обычно общий вид подобных уравнений следующий:
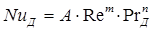. (1.18)
В нем NuД = βl/D — диффузионный критерий Нуссельта; Re = wlρ/μ = wl/v — критерий Рейнольдса; РrД = μ/ρD = v/D — диффузионный критерий Прандтля.
Величины коэффициента А и показателей степени m ип определяются в результате обработки экспериментальных данных.
В процессе перегонки происходит частичное испарение исходной смеси с целью получения одного из продуктов, например, обогащенного низкокипящим компонентом (НКК). Различают постепенное, однократное и многократное испарение смесей. Образующийся при перегонке отгон, продукт, обогащенный НКК, в дальнейшем подвергают конденсации. Процесс постепенного испарения осуществляют так, что образовавшаяся в процессе испарения паровая фаза непрерывно удаляется из системы в момент ее образования. При этом принимают, что сосуществующие в системе фазы находятся в состоянии равновесия.
Процессы однократного испарения (ОИ) осуществляют таким образом, чтобы образовавшаяся в системе паровая фаза оставалась в ней до наступления состояния равновесия. Многократный процесс испарения или конденсации состоит в повторении несколько раз процессов ОИ с целью более полного разделения исходной смеси.
В нефте- и газопереработке приходится разделять сложные и многокомпонентные углеводородные смеси. При разделении таких смесей ОИ любой компонент будет распределяться в определенном соотношении между паровой и жидкой фазами. Материальный баланс процесса ОИ для любого компонента запишется в виде
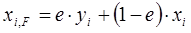. (1.19)
Образовавшаяся паровая фаза состава уi находится в равновесии с жидким остатком состава хi. Тогда уравнение (1.19) можно записать в следующем виде:
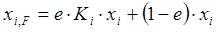, (1.20)
откуда
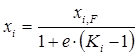. (1.21)
Просуммировав концентрации по всем компонентам, получим
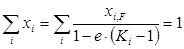. (1.22)
Из уравнения (1.22) методом последовательных приближений можно определить долю отгона е при заданных температуре и давлении. При полном испарении смеси е=1 и
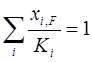. (1.23)
Уравнение (1.23) является уравнением изотермы паровой фазы и позволяет определить температуру начала конденсации паров при заданном давлении p [3].
Если в уравнении (1.19) выразить xi через уi, согласно уравнению равновесия, то
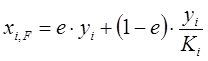, или 
. (1.23)
Сложив составы всех компонентов паровой фазы, получим
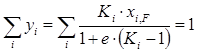. (1.24)
Полученное уравнение также можно использовать для определения доли отгона смеси е. Оно дает большую точность, чем уравнение (1.22) при малых долях отгона. Из уравнения (1.25) можно найти температуру кипения смеси при е=0, которое является уравнением изотермы жидкой фазы
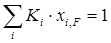. (1.26)
Литература:
1. Касаткин А. Г. Основные процессы и аппараты химической технологии. М.: Химия, 1991. — 783 с.
2. Дытнерский Ю. И. Процессы и аппараты химической технологии: Учебник для вузов: В 2 кн. М.: Химия, 1995. — 368 с.
3. Молоканов Ю. К. Процессы и аппараты нефтегазопереработки. М.: Химия, 1980.- 407 с.
4. Плановский А. Н., Николаев П. И. Процессы и аппараты химической и нефтехимической технологии. 3-е изд. перераб. и доп. М.: Химия, 1987. — 496 с.
5. Коган В. Б. Теоретические основы типовых процессов химической технологии. М.: Химия, 1977. — 546 с.
