Поведение многих объектов описывается так называемой конечно-автоматной моделью. В соответствии с этой моделью объект находится в одном из конечного множества состояний, а переходит в другое состояние под воздействием входных сигналов (команд, событий). Находясь в том или ином состоянии, объект вырабатывает некий выходной сигнал (параметр). Иначе говоря, конечный автомат — математическая (алгоритмическая) модель поведения устройств с конечной памятью. Конечные автоматы применяются, например, в системах синтаксического анализа и перевода текста, компьютерных играх, системах управления сложными техническими устройствами и др.
Абстрактный автомат — это математическая модель, описывающая техническое устройство совокупностью входных, выходных сигналов и состояний, кроме того: имеет множество внутренних состояний A={a1(t), a2(t),…,aM(t)}, называемых состояниями автомата; на вход автомата поступает конечное множество входных сигналов Z={z1(t), z2(t),…,zF(t)}; имеется конечное множество выходных сигналов W={u1, u2,…,uG}; задана функция перехода δ(am,zi); задана функция формирования выходов автомата λ(am,zi); определено начальное состояние автомата a1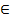
A.
То есть для описания автомата нужно использовать шестёрку вида S={A, Z, W, δ, λ, a1}, где
- A={a1, a2,…,aM} — алфавит состояний;
- Z={z1, z2,…,zF} — входной алфавит;
- W={u1, u2,…,uG} — выходной алфавит;
- δ: A×Z→A (as=δ(am,zi)/as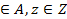
);
- λ: A×Z→W (us=λ(am,zi)/ as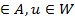
);
- a1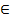A
Автомат реализует некоторое отображение множества слов входного алфавита Z в множество слов выходного алфавита W.
В зависимости от способа определения выходного сигнала в синхронных автоматах различают:
1. Автомат первого рода (Автомат Мили)
A(t+1)=δ(a(t), z(t));
W(t)=λ(a(t), z(t)); где t=0, 1, 2…
2. Автомат второго рода (Автомат Мура)
A(t+1)=δ(a(t), z(t));
W(t)=λ(a(t), z(t)); где t=0, 1, 2…
W(t+1)=λ(a(t+1))= λ (δ(a(t), z(t))
Методы задания автоматов
Для задания конечного автомата S требуется описать все элементы множества S={A, Z, W, δ, λ}. Наиболее часто используемой формой описания элементов множества S используется табличный, графический, матричный способы.
Теоретико-множественное представление автоматов.
Для задания конечного автомата S={A, Z, W, δ, λ} все элементы множества должны быть заданы явно. Так для автомата Мили:
A={a1, a2,…,aM} — алфавит состояний;
Z={z1, z2,…,zF} — входной алфавит;
W={u1, u2,…,uG} — выходной алфавит;
δ: A×Z→A (as=δ(am,zi)/as);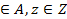
λ: A×Z→W (us=λ(am,zi)/ as);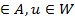
a1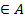
- начальное состояние автомата.
Например, автомат Мили S1={A, Z, W, δ, λ, а1}, представленный в табл.1.3 в явной форме описывается так:
A={a1, a2, a3}; Z={z1, z2}; W={u1, u2}; δ: a2=δ(a1,z1); a3=δ(a1,z2); a1=δ(a2,z1); a3=δ(a2,z2); a3=δ(a3,z1); a2=δ(a3,z2); λ: u1=λ(a1,z1); u2=λ(a1,z2); u2=λ(a2,z1); u1=λ(a2,z2); u1=λ(a3,z1); u1=λ(a3,z2).
Автомат Мура S2={A, Z, W, δ, λ, а1}, представленный в табл.1.8 в явной форме описывается так:
A={a1, a2, a3, a4, a5}; Z={z1, z2, z3}; W={u1, u2, u3}; δ: a2=δ(a1,z1); a1=δ(a1,z2); a4=δ(a2,z3); a1=δ(a2,z1); a5=δ(a2,z2); a3=δ(a2,z3); a1=δ(a3,z1); a2=δ(a3,z2); a5=δ(a3,z3); a1=δ(a4,z1); a5=δ(a4,z2); a2=δ(a4,z3); a1=δ(a5,z1); a3=δ(a5); a4=δ(a5,z3); λ: u1=λ(a1); u3=λ(a2); u2=λ(a3); u1=λ(a4); u3=λ(a5).
Табличная форма.
Табличная форма для автомата Мили иллюстрируется табл.1.1 (переходов) и табл.1.2 (выходов).
|
Таблица 1.1
|
Таблица 1.2
|
zf\a m |
a1 |
… |
aM |
|
z1 |
λ(а1, z1) |
… |
λ(аM,z1) |
|
… |
… |
… |
… |
|
zF |
λ(a1,zF) |
… |
λ(aM,zF) |
Строки этих таблиц соответствуют входным сигналам, а столбцы — состояниям, причем крайний левый столбец обозначен начальным состоянием a1. На пересечении столбца am и строки zf…. в таблице переходов ставится функция перехода δ(am,zf), то есть состояние, в которое автомат переходит из состояния am под действием входного сигнала zf, а в таблице выходов — выходная функция λ(am,zf), то есть соответствующий этому переходу выходной сигнал ug.
Пример табличного способа задания автомата Мили показан в табл. 1.3 (переходов) и табл. 1.4 (выходов).
Таблица 1.3
|
zf\a m |
a1 |
a2 |
a3 |
|
z1 |
a2 |
a1 |
a3 |
|
z2 |
a3 |
a3 |
a2 |
Таблица 1.4
|
zf /a m |
a1 |
a2 |
a3 |
|
z1 |
u1 |
u2 |
u1 |
|
z2 |
u2 |
u2 |
u2 |
Таблица 1.5
|
z f\ am |
a 1 |
a2 |
a 3 |
a 4 |
|
z1 |
a 2 |
a 1 |
a 3 |
- |
|
z2 |
a 3 |
a 3 |
a - |
a 1 |
|
z3 |
- |
a4 |
a2 |
a4 |
Таблица 1.6
|
z f\a m |
a 1 |
a2 |
a 3 |
a 4 |
|
z1 |
u1 |
u 2 |
u 1 |
- |
|
z2 |
u 2 |
u1 |
- |
u 2 |
|
z3 |
- |
u1 |
u2 |
u1 |
Автомат называется частично заданным, если он определен не для всех пар переходов (am, zf). Для частично заданного автомата на месте отсутствующего перехода ставится прочерк как в таблице переходов, так и в таблице выходов.
Пример табличного способа задания частичного автомата показан в табл.1.5 (переходов) и табл.1.6 (выходов).
Табличная форма задания автомата Мура представляет собой совмещенную табл.1.7, в которой выходной сигнал, соответствующий состоянию в am автомате Мура размещен в верхней строке над соответствующими состоянием, а остальная информация аналогична представлению автомата Мили. Пример представления автомата Мура приведен в табл.1.8.
Таблица 1.7
|
uG |
u1 |
… |
uG |
|
zf\ am |
a 1 |
… |
am |
|
z1 |
δ(a1,z1) |
… |
δ(aM,z1) |
|
… |
… |
… |
… |
|
zF |
δ(a1,zF) |
… |
δ(aM,zF) |
|
Таблица 1.8 |
|||||
|
uG |
u1 |
u3 |
u2 |
u1 |
u3 |
|
zf\ am |
a 1 |
a2 |
a3 |
a4 |
a5 |
|
z1 |
a2 |
a1 |
a1 |
a1 |
a1 |
|
z2 |
a3 |
a5 |
a2 |
a5 |
a3 |
|
z3 |
a4 |
a3 |
a5 |
a2 |
a4 |
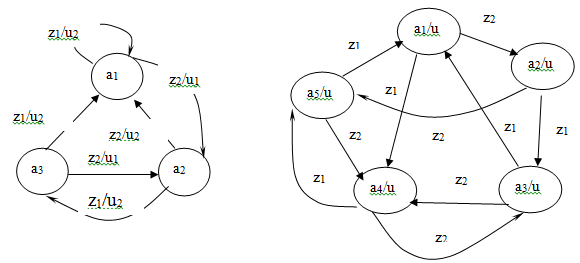
Графовая форма задания абстрактных автоматов
В данном случае автомат S={A, Z, W, δ, λ, а1} представляется графом, в котором:
1. множество A изображено вершинами графа;
2. функция δ задана дугами графа, причем две вершины графа am и as, соединяются дугой, если в автомате существует переход из am в as;
3. множество Z изображено метками дуг: zf ставится на дуге из вершины am в вершину as, если в автомате существует переход из am в as под действием входного сигнала zf;
4. функция λ задана метками дуг или вершин: для автомата Мили дуга из вершины am в вершину as помечается выходным сигналом ug, если в автомате существует переход из am в as и при этом вырабатывается выходной сигнал ug; а для автомата Мура выходным сигналом ug помечается вершина, определяющая as=λ(am).
На рис.1 приведены примеры описания автомата Мили и автомата Мура:
Матричная форма
Для автомата Мили матричная форма состоит из матрицы C=׀cms׀ размерностью M×M, где каждый элемент матрицы cms=zf/ug, стоящий на пересечении m-ой строки и s-го столбца соответствует входному сигналу zf, вызывающему переход из состояния am в состояние as с выработкой выходного сигнала ug.
Пример матричного описания автомата Мили показан ниже.
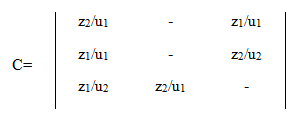
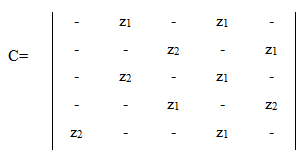
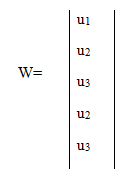
Для автомата Мура матричная форма состоит из матрицы C=׀cms׀ размерностью M×M, где каждый элемент матрицы cms=zf, стоящий на пересечении m-ой строки и s-го столбца, соответствует входному сигналу zf, вызывающему переход из состояния am в состояние as. Так как выходной сигнал ug в автомате Мура зависит только от состояния, следовательно, выходные сигналы могут быть представлены матрицей-столбцом. Пример матричного описания автомата Мура показан на формуле, приведенной выше.
Наконец, для задания абстрактных автоматов можно использовать различные операции, выражающие одни автоматы через другие. В качестве примера такой операции рассмотрим сумму S+P автоматов, где S={A, Z, W, δ, λ} и P={Aʹ, Z, W, δʹ, λʹ}, где A
Aʹ=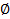
. Полагаем, S+P={A.
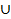Aʹ, Z, W, δʹʹ, λʹʹ}, где δʹʹ(a,z)=δ(a,z), λʹʹ(a,z)=λ(a,z) при a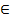A, z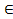
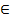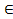Z и δʹʹ(a,z)=δʹ(a,z), λʹʹ(a,z)=λʹ(a,z) при aAʹ, zZ.
Литература:
1. Брауэр В. Введение в теорию конечных автоматов.- М.: Радио и связь, 1987,-392с.
2. Карпов Ю. Г. Теория автоматов.-СПб.: Питер, 2002,-204с.
3. Кудрявцев В. Б., Алешин С. В., Подколзин А. С. Введение в теорию автоматов.-М.: Наука, 1985,-320с.
4. Математическая энциклопедия. Ред. коллегия: И. М. Виноградов (гл. ред.) [и др.]. Т.1 — М.: Советская энциклопедия, 1977. — 1152 стб.
5. Трахтенброт Б. А., Барздинь Я. М. Конечные автоматы (поведение и синтез).-М.: Наука, 1970,-400с.
6. Тюрин С. В. Элементы теории автоматов (Часть 1): Учебное пособие. Воронеж: Воронеж. гос. техн. ун-т, 2002. 98 с.
7. Пентус А. Е., Пентус М. Р. Математическая теория формальных языков. БИНОМ. Лаборатория знаний, Интернет университет информационных технологий — ИНТУИТ.ру, 2006,-248с.
8. Хопкрофт Дж.Э., Мотвани Р., Ульман Дж.Д. Введение в теорию автоматов, языков и вычислений, 2-у изд.-М.: Вильямс, 2002,-528с.
