В статье рассматриваются вопросы, связанные с особенностями применения статистических критериев проверки гипотез к обработке экспериментальных данных больших объемов, в частности, к обработке данных социологических исследований. Приводятся особенности реализации и сравнительная характеристика параметрических и непараметрических критериев проверки гипотез.
Ключевые слова:выборка, генеральная совокупность, статистические критерии проверки гипотез, параметрические и непараметрические критерии.
Одной из важнейших задач математической статистики на сегодняшний день является разработка и применение эффективных методов анализа статистических данных, полученных в разных областях деятельности человека. Но существует ряд особенностей применения методов математической статистики для обработки данных социально-психологических исследований. Во-первых, значительное количество измерений случайных величин, характеризующих те или иные стороны социально-психологических явлений и процессов производится в номинальной и порядковой шкалах, где затруднено применение многих параметрических методов. Во-вторых, часто, особенно в социологии, необходимо провести статистическую обработку данных очень больших объемов. И, в-третьих, почти всегда неизвестны и не могут быть установлены с помощью качественного анализа типы вероятностных законов распределения упомянутых выше случайных величин.
Указанные особенности не позволяют исследователям применять в своей работе методы математической статистики по аналогии с тем, как эти методы применяются в естественных или технических науках.
Непараметрические методы расширяют область приложения статистических методов в социально-психологических науках по сравнению с классическими параметрическими методами, так как «…не предназначены специально для какого-нибудь параметрического семейства распределений и не используют его свойства» [5, с.6].
В основе любого непараметрического критерия лежит определенная непараметрическая статистика.
Рассмотрим выборочный вектор х=(x1,...,xn) из генеральной совокупности, характеризуемой случайной величиной Х=(X1,…,Xn). Пусть F0 — функция распределения случайной величины Х.
Определение 1. Статистика S(Х) называется непараметрической, если распределение S(Х) не зависит от F0 [1, с.70].
В целях обобщения и систематизации непараметрических критериев проверки гипотез рассмотрим классификацию непараметрических статистик, в основу которой положен способ вычисления этих статистик.
Все непараметрические статистики можно разделить на две группы:
1. ранговые непараметрические статистики;
2. неранговые непараметрические статистики.
Первую группу «Ранговые непараметрические статистики» мы разделяем ещё на две подгруппы:
1.1. непараметрические статистики, основанные на эмпирических функциях распределения;
1.2. собственно ранговые непараметрические статистики.
Рассмотрим более подробно первую группу методов — «Ранговые непараметрические статистики». Вычисление статистик данной группы базируется на понятии ранга, поэтому введем соответствующие определения.
Определение 2. Пусть оi(x) есть значение i-й по величине координаты вектора x=(x1,…,xn), так что o1(x) — наименьшее значение, on(x) — наибольшее. Полагая x(i)=oi(x), имеем
x(1) ≤ x(2) ≤ …≤x(n). (1)
Статистика X(i)=oi(Х) будет называться i-й порядковой статистикой, и вектор порядковых статистик (X(1),…,X(n)) будет кратко обозначаться X(.) [2, с.45].
Определение 3. Для вектора x=(x1,…,xn), у которого никакие две координаты не совпадают, обозначим ri(x) — число координат, не превосходящих xi, то есть номер xi в последовательности (1), тогда статистику
Ri=ri(Х), i=1, …, n
будем называть рангом элемента Xi. Вектор R=(R1,…,Rn) будет обозначать вектор рангов [2, с.45].
Очевидно, что по определению 3 числа ri(x) образуют перестановку порядка n.
Определение 4. Статистику Т, являющуюся функцией от R, T=t(R), будем называть ранговой статистикой [2, с.71].
Определение ранговых статистик в статье основано на существенном предположении, что все наблюдаемые случайные величины имеют непрерывные распределения. Однако случайные величины, наблюдаемые на практике всегда дискретны либо по своей природе (например, целочисленные величины), либо вследствие округления. Существуют способы специальной обработки экспериментальных данных так, чтобы можно было применить теорию ранговых статистик, например, рандомизация, усредненные статистики и метки, средние ранги и т. д.
Остановимся более подробно на группе методов, составляющих подгруппу 1.1 «Непараметрические статистики, основанные на эмпирических функциях распределения».
Определение 5. Статистики типа Колмогорова-Смирнова будем называть статистиками, основанными на эмпирических функциях распределения.
Подгруппа 1.1 включает в себя статистику Колмогорова, статистику Смирнова, Реньи, статистику Крамера-Мизеса и другие. Покажем на примере статистики Смирнова, что статистики этой подгруппы действительно являются ранговыми.
Определение 6. Пусть (d1,...,dn) — обратная перестановка по отношению к (r1,...,rn), то есть
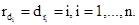
Пусть D = (D1,...,Dn) обратна в этом смысле к R=(R1,...,Rn), тогда статистики D1,...,Dn будем называть антирангами [2, с.77].
Пусть X1,...,Xm — первая выборка объема m; X1,...,Xn — вторая выборка объема n; D1,...,Dn+m — антиранги для объединенной выборки X1,...,Xn+m. Из определений 1 и 3 ясно, что Dk=j тогда и только тогда, когда X(k)=Xj. Обозначим F1,m(x) и F2,n(x) — эмпирические функции распределения для первой и второй выборок соответственно. Положим
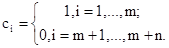
Предложение 1. Статистику Смирнова
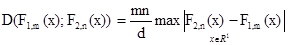 (2)
(2)
можно представить в виде:

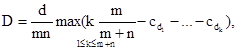
где d — наибольший общий делитель n и m.
Доказательство приводится в [6, с.64].
На основе статистик данной подгруппы разработаны широко известные критерии проверки гипотез Колмогорова, Смирнова, Реньи, Крамера-Мизеса. В частности, критерий Колмогорова предназначен для проверки гипотез согласия. Критерии Смирнова, Реньи и Крамера-Мизеса предназначены для проверки гипотез однородности двух независимых выборок, причем как отмечают Я. Гаек и З. Шидак в [2] альтернативы могут быть как широкими, так и более узкими, например, о сдвиге функции плотности одной выборки относительно функции плотности другой или о различии параметров масштаба в двух выборках.
Наиболее широко в социально-психологических исследованиях используются критерии Колмогорова и Смирнова, в источнике [4] рекомендуется применять их для выявления различий в распределении исследуемых социально-психологических признаков при самых общих альтернативах. Но при этом следует учитывать некоторые особенности. В работе [3] авторы утверждают, что критерий Смирнова допускает использование данных, измеренных по шкале не ниже порядковой, однако для порядковых статистик таблицы точных критических значений составлены, в основном, для выборок небольшого объема, поэтому при выборках большого объема приходится пользоваться таблицами критических значений предельного распределения Колмогорова. Переход к предельному распределению возможен только в том случае, когда экспериментальные данные представляют измерения по шкале не ниже интервальной. Поэтому чаще всего в социально-психологических исследованиях применение критерия Смирнова возможно в случае оценки результатов социально-психологических экспериментов для двух независимых выборок при учете времени изучаемых реакций или числа верных (или неверных) ответов испытуемых на контрольные вопросы, так как эти измерения производятся по интервальной шкале.
Так как в процессе использования критерия Колмогорова для проверки гипотезы согласия в случае выборок большого объема также осуществляется переход к предельному распределению Колмогорова, то и для этого критерия верно вышесказанное замечание об использовании интервальной шкалы.
В работе [3, с.123–124] авторы сравнивают критерии Смирнова и χ2 для проверки гипотез однородности при самых общих альтернативах и приходят к выводу, что область применения критерия χ2 шире, так как он допускает использование данных, измеренных по шкале наименований, причем с любым числом категорий. В то же время, критерий Смирнова более чувствителен, позволяя в ряде случаев отклонять нулевую гипотезу при более низком уровне значимости, чем χ2. Других сравнений для методов данной группы не найдено.
Таким образом, проведенный анализ показал, что, основываясь на особенностях социально-психологических измерений, все непараметрические статистики можно разделить на 2 группы: ранговые и неранговые. Методы, основанные на статистиках группы «Ранговые непараметрические статистики» применимы к широкому кругу задач: проверка согласия, однородности, независимости, симметричности распределения выборок; оценка и определение доверительных интервалов для параметров сдвига и масштаба и т. д. Методы этой группы имеют высокую чувствительность, но область применения их в психологии ограничена порядковыми, а для первой подгруппы даже интервальными, данными.
Методы проверки гипотез группы «Неранговые непараметрические статистики» ещё предстоит исследовать, хотя круг задач этих методов более узок: в основном проверка согласия и однородности распределений выборок. С другой стороны, методы, основанные на ядерных оценках плотности, работают лишь с данными, измеренными по шкале интервалов или отношений, но они решают более сложные задачи, например, задачу распознавания образов в условиях неоднозначных указаний «учителя».
Литература:
1. Боровков А. А. Математическая статистика. — Новосибирск: Наука. Изд-во Института математики, 1997.– 772 с.
2. Гаек Я., Шидак З. Теория ранговых критериев. — М.: Наука, 1971.– 371с.
3. Грабарь М. И., Краснянская К. А. Применение математической статистики в педагогических исследованиях. Непараметрические методы. — М.: Педагогика, 1977.-136 с.
4. Сидоренко Е. В. Методы математической обработки в психологии.-СПб.: Соц.-пс. центр, 1996.-349 с.
5. Холлендер М., Вулф Д. Непараметрические методы статистики/ Пер. с англ. Д. С. Шмерлинга; Науч. ред. Ю. П. Адлера, Ю. Н. Тюрина. — М.: Финансы и статистика, 1983.-518 с.
6. Hajek J. Nonparametric Statistics. Holden-Day, San Francisco, 1969.







