В данной работе с помощью изучения общих свойств когомологии простых модулей простых односвязных алгебраических групп и их алгебр Ли в положительной характеристике найдены нетривиальные примеры вторых групп когомологий простых модулей классических алгебр Ли в положительной характеристике. Пусть 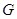 – простая односвязная алгебраическая группа над алгебраически замкнутым полем
– простая односвязная алгебраическая группа над алгебраически замкнутым полем 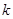 характеристики
характеристики 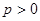 и
и 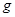 – ее алгебра Ли. Для доказательства основного результата будем пользоваться свойством отображения Фробениуса на
– ее алгебра Ли. Для доказательства основного результата будем пользоваться свойством отображения Фробениуса на 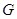 и теоремой Стейнберга о тензорном произведений. Отображение Фробениуса на
и теоремой Стейнберга о тензорном произведений. Отображение Фробениуса на 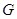 позволяет вычислить когомологию простых модулей группы
позволяет вычислить когомологию простых модулей группы 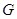 с помощью спектральной последовательности Линдона-Серра-Хохшильда. Предположим, что
с помощью спектральной последовательности Линдона-Серра-Хохшильда. Предположим, что 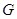 определена над простым подполем
определена над простым подполем 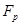 поля
поля 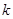 . Это означает, что существует алгебраическая
. Это означает, что существует алгебраическая 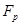 -группа
-группа 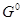 такая, что
такая, что 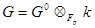 . Тогда отображение
. Тогда отображение 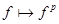 на
на 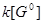 является эндоморфизмом
является эндоморфизмом 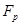 -алгебр и индуцирует отображение
-алгебр и индуцирует отображение 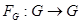 .
.  является групповым эндоморфизмом и называется отображением (морфизмом) Фробениуса. Ядро
является групповым эндоморфизмом и называется отображением (морфизмом) Фробениуса. Ядро 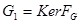 называется ядром Фробениуса. Ядро Фробениуса являются инфинитезимальной подгруппой группы
называется ядром Фробениуса. Ядро Фробениуса являются инфинитезимальной подгруппой группы 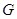 .
.
Используя результаты работы [1], можно найти некоторые нетривиальные примеры вторых групп когомологий простых модулей классических алгебр Ли в положительной характеристике. По предложению 2.1 работы [1], стр. 407,
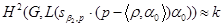 , (1)
, (1)
где 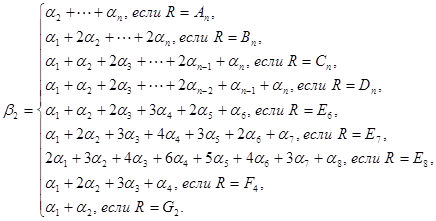 (2)
(2)
Предложение 1. Пусть 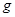 – простая алгебра Ли простой односвязной алгебраической группы
– простая алгебра Ли простой односвязной алгебраической группы 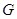 над алгебраически замкнутым полем
над алгебраически замкнутым полем 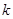 характеристики
характеристики 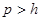 . Предположим, что
. Предположим, что 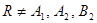 . Тогда
. Тогда  , где
, где 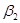 задается равенством (2).
задается равенством (2).
Доказательство. Пусть 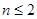 , где
, где 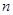 – ранг системы
– ранг системы 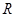 . Для алгебр Ли
. Для алгебр Ли 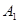 и
и 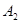
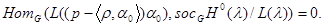 Следовательно, в этом случае, вторые когомологий группы и алгебры Ли не совпадают. Если
Следовательно, в этом случае, вторые когомологий группы и алгебры Ли не совпадают. Если 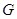 имеет систему корней типа
имеет систему корней типа 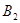 , то
, то 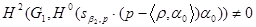 , что противоречить условию
, что противоречить условию 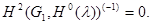 В случае
В случае 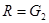 и
и 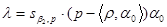
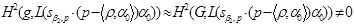 .
.
Далее, используя (1), получим 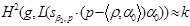 .
.
Таким образом, среди классических алгебр Ли ранга 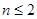 , только в случае алгебры Ли типа
, только в случае алгебры Ли типа 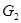 имеется совпадения второй группы когомологии с соответствующей второй группой когомологии алгебраической группы.
имеется совпадения второй группы когомологии с соответствующей второй группой когомологии алгебраической группы.
Пусть теперь, 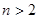 . Тогда условие предложения 2.1 работы [1], стр. 407, обеспечивает выполнения условий
. Тогда условие предложения 2.1 работы [1], стр. 407, обеспечивает выполнения условий
1) 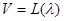 , где
, где 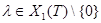 ;
;
2)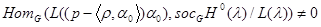 ;
;
3)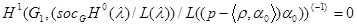 .
.
Поэтому, проверим только выполнение условия 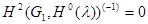 .Произведя соответствующие вычисления, получим
.Произведя соответствующие вычисления, получим
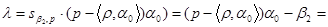

за исключением, когда 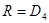 и
и 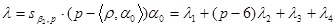 . Согласно общей формуле Андерсена-Янцена [2],
. Согласно общей формуле Андерсена-Янцена [2], 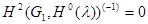 . Таким образом, согласно (1), получим
. Таким образом, согласно (1), получим 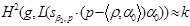 . Предложение 1 доказано.
. Предложение 1 доказано.
Для систем корней малых рангов легко можно описать все одинаковые нетривиальные вторые группы когомологий простых модулей простых односвязных алгебраических групп и их алгебр Ли.
1. В случае 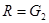 , используя результаты работы [3], относительно структуры
, используя результаты работы [3], относительно структуры 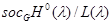 ,
, 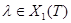 , легко показать, что полученный, в Предложении 1 случай, является единственным нетривиальным примером совпадения соответствующих вторых групп когомологий простых модулей группы
, легко показать, что полученный, в Предложении 1 случай, является единственным нетривиальным примером совпадения соответствующих вторых групп когомологий простых модулей группы 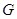 и алгебры Ли
и алгебры Ли 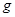 .
.
2. В случае 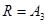 имеются ровно 2 совпадения. Первый – это пример Предложения 1, когда старший вес простого модуля равен
имеются ровно 2 совпадения. Первый – это пример Предложения 1, когда старший вес простого модуля равен 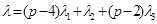 , второй –
, второй – 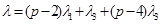 . Здесь достаточно использовать результаты работы [4], стр.94 - 98.
. Здесь достаточно использовать результаты работы [4], стр.94 - 98.
3. Точность последовательности (6) и предложение 6 работы [5] показывают, что в случае 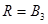 также имеются ровно два совпадения нетривиальных вторых групп когомологий. Старшие веса соответствующих простых модулей равны
также имеются ровно два совпадения нетривиальных вторых групп когомологий. Старшие веса соответствующих простых модулей равны 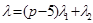 и
и 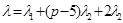 .
.
Литература:
1. O’Halloran J. Weyl modules and cohomology of Chevalley groups // Amer. J. of Math. -1981. - Vol. 103, № 2. - P. 399-410.
2. Andersen H.H., Jantzen J.C. Cohomology of induced representations for algebraic groups // Math. Annalen. - 1984. - Vol. 269. - P. 487-525.
3. Jantzen J.C. Darstellungen halbeinfascher gruppen und contravariante formen // J. reine angew. Math. - 1977. - V. 290. - P. 117-141.
4. Jantzen J.C. Weyl modules for groups of Lie type in M. Collins ed., Finite simple groups. London, New York: Acad. Press, 1980. P. 291-300.
5. Ибраев Ш.Ш. О когомологии простых модулей для ядра Фробениуса // «Бәсекеге қабілетті жеке тұлғаны қалыптастырудағы жаратылыстану-математикалық пәндерді оқытудың өзекті мәселелері» халықаралық ғылыми-практикалық конф. материалдары: ҚОББҚБАҚДИ (19-20 қараша 2010ж.). - Кызылорда.- 2011. - С. 363-368.







