Для решения вопросов задачи исследования и определения направления совершенствования технологии транспортирования, сушки распределения хлопка, а также обоснования геометрических и кинематических параметров устройства транспортирования хлопка-сырца в области применения, необходимо изучить теоретические основы процесса транспортирования.
Процесс транспортирования хлопка-сырца осуществляется при помощи вращающихся винтов или перемещающейся ленты. Изучением внутреннего трения хлопка сырца по различным поверхностям занимались многие исследователи.
Величина сопротивления сдвигу хлопка-сырца, характеризующаяся величину внутреннего трения и сцепления выражается следующим уравнением (рис.1):
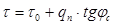, н/м2 (1)
где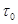 
— внутреннее трение хлопка сырца; 
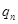- нормальное давление хлопка сырца. Нам известно, что зависимость между сопротивлением сдвигу хлопка — сырца по хлопку — сырец и нормальным давлением выражается следующим эмпирическим уравнением:
,
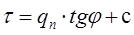С — структурное сплетение хлопка-сырца. Сопротивление сдвигу хлопка-сырца, в зависимости от плотности, экспериментально определяется следующим уравнением [1]:
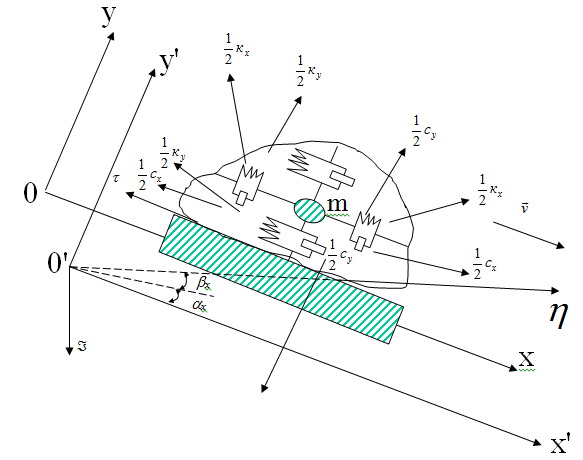
Рис. 1. Упруго-вязкоупругая модель хлопка-сырца, где: О1Х1У1 — подвижная система координат; ОХУ — неподвижная система координат
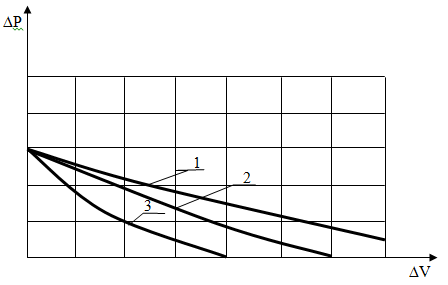
Рис. 2. Зависимость давления хлопка-сырца от скорости. 1 — кх=ку=0,001, 2 — кх=ку=0,01, 3 — кх=ку=0,1
,
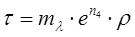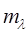и 
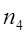— постоянные зависящие от влажности хлопка-сырца.
Рассмотрим общий случай транспортирования хлопка-сырца (моделируемая как вязко-упругая механическая система) грузонесущему органу транспортирующей машины (рис.1) совершающего движения, направленные под углом b к наложенному под углом a к горизонту грузонесущему органу.
Общие затрат энергии машиной, связанное с процессом транспортирования хлопка-сырца будет:
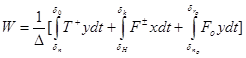(2)
где, D — продолжительность цикла движения;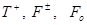 
— действующие и нормальные сдвиговые силы; 
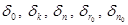и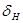 
- верхние и нижние значения продолжительности действующей силы.
С помощью уравнение Лагранжа 2-го рода можно записать уравнения движения хлопка-сырца на участке упругой деформации на подвижные оси ху:
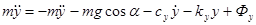
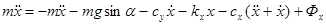(3)
где, m — масса летучей хлопка-сырца;
kу,kx — коэффициент жесткости упругих элементов;
су, сх — коэффициенты трения;
Фу и Фх — действующие внешние кинематические воздействия.
; 
; 
, 
.
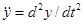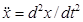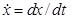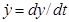По результатам исследования установлено, что увеличение влажности хлопка-сырца в пределах от 11 до 38 % сопровождается повышением коэффициента трения покоя и движения. С повышением удельной нагрузки на хлопок-сырец, величина коэффициента трения снижается, а с увеличением скорости скольжения поверхности от 0 до 0,54 м/с, коэффициент трения снижается сравнительно резко.
Дальнейшее увеличение скорости сопровождается незначительным снижением коэффициента трения и приближением его к некоторой постоянной величине. Системы дифференциального уравнения решается численно методом Рунге-Кута. Зависимость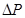 
(давления) от скорости 
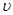приведена на рис. 2. Из рисунка видно, что 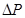сильно зависит от внутреннего трения хлопка-сырца (влажность, засоренность и др.).
Проведенные исследования с композиционными полимерными покрытиями рабочих органов транспортирующих средств показали, что с повышением скорости до определенной величины для всех нормальных давлений коэффициент трения повышается, а затем несколько понижается и принимает постепенное значение. С увеличением влажности до 14–16 % коэффициент трения повышается, а затем с дальнейшим увеличением влажности — снижается.
Литература:
1. Х. К. Рахмонов. Разработка рациональной технологии распределения хлопка-сырца при его складировании. Автореферат. Тошкент.1996 й.
2. Р. Л. Зенков и др. Машины непрерывного транспорта. М. 1982.
