Электромагнитные цепи относятся к цепям с существенными нелинейными элементами, и исследования установившихся режимов и переходных процессов связаны со значительными математическими выкладками. Анализ установившегося режима электромагнитной цепи удобно вести методом, изложенным в монографии М.Г. Александровой и др. [1], согласно которому цепь представляется как линейный многополюсник с одним входом и выходами, состоящими из нелинейных ферромагнитных элементов.
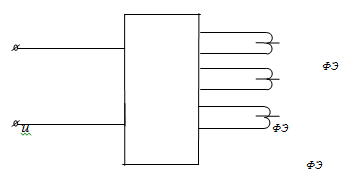
Рис. 1
Дифференциальные уравнения состояния для цепи с одним ферромагнитным элементом при аппроксимации кривой намагничивания с соотношением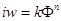 
имеет следующий вид
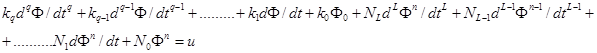(1)
Коэффициенты уравнения (1) определяются при помощи параметров многополюсника для конкретной цепи. Для электроферромагнитного контура, показанного на рис. 2, справедливо следующее уравнение.
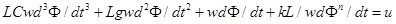(2)
Здесь u-приложенное напряжение;
w-число витков обмотки ферромагнитного элемента;
Ф- магнитные потоки в сердечниках ферромагнитных элементов;
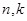- степень и коэффициент аппроксимирующей функции;
После ведения базисных величин получим:
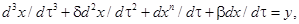(3)
где
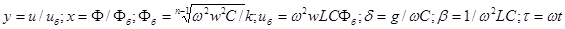
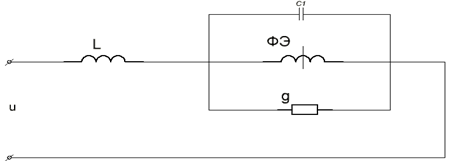
Рис. 2
Таким образом, вместо уравнения (2), мы имеем нелинейное безразмерное дифференциальное уравнение (3) с минимальным количеством коэффициентов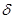 
и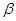 
. Это достигнуто удачным выбором значений базисных величин 
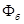и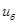 
. Далее уравнение (3) легко решается методом учета основной гармоники магнитного потока или методом медленно меняющихся амплитуд, на основе которых легко получить необходимые характеристики [4].
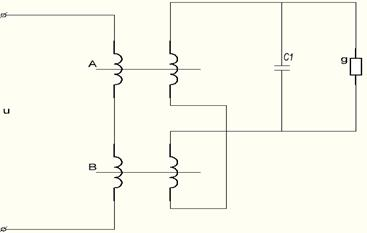
Рис. 3.
Другим примером может служить составление нормированного уравнения состояния для двухсердечниковой параметрической цепи (рис.3), для которой справедливо следующее уравнение:
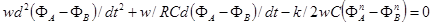
После введения базисных величин и аппроксимации кривой намагничивания ферромагнитного элемента кубической функцией, это уравнение примет следующий вид:
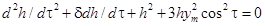(4)
Здесь принято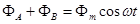 
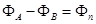
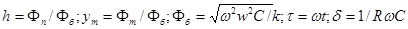
Полученное уравнение (4) с единственным коэффициентом 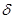можно решить, применяя асимптотический метод Крылова-Боголюбова-Митропольского. В первом приближении, допуская 
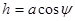, мы получим:
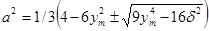(5)
Задаваясь значением y для определенного 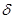, мы можем исследовать основные характеристики электромагнитной цепи. При этом необязательно определение численного значения коэффициента аппроксимирующей функции.
Известно, что электроферромагнитные цепи широко используются в качестве стабилизаторов тока, напряжения или преобразователей частоты [2, 3]. Например, электроферромагнитная цепь, показанная на рис. 1, применяется в цепи управления ферромагнитного удвоителя частоты со стабилизацией выходного напряжения. В этом случае, в качестве нагрузки служит активное сопротивление цепи управления ферромагнитного удвоителя частоты по схеме Жоли-Эпштейна. Уравнение состояния имеет следующий вид:
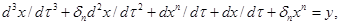(6)
Здесь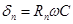 
- коэффициент, пропорциональный величине активной нагрузки, которая включается последовательно с линейной индуктивностью. При составлении уравнения (6) не учитываются потери в параллельном ферромагнитном контуре.
Принимая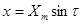 
из (6)для случая n=9, имеем:
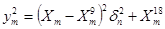
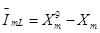
Здесь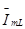 
- относительное максимальное значение тока нагрузки.
В режиме стабилизации выходного напряжения удвоенной частоты значение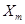 
изменится в пределах от 0,8 до 1. Исследование соотношений установленных мощностей показали, что
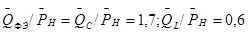
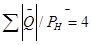
Здесь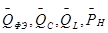 
- соответственно относительные максимальные мощности ферромагнитного элемента, ёмкости, линейной индуктивности и активной нагрузки. Таким образом, общая мощность реактивных элементов цепи превышает мощность нагрузки в четыре раза.
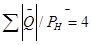
Эти соотношения являются базовыми величинами при расчете элементов электроферромагнитной цепи.
Выводы.
1. Приведение уравнений состояния электроферромагнитной цепи к базисным условиям позволяет получить нормированное дифференциальное уравнение с минимальным количеством коэффициентов. При этом появляется возможность анализировать режимы электроферромагнитной цепи без определения значения коэффициента аппроксимации кривой намагничивания.
2. На основе нормированных соотношений определяются удельные значения мощностей элементов цепи электроферромагнитных устройств.
Литература:
1. Александрова М. Г., Белянин А. Н. и др. Расчёт электрических цепей и электромагнитных полей. М, Радио и связь, 1983, 344 стр.
2. Кадыров Т. М., Алимов Х. А., Файзиев М. М.-Магнитные усилители с электроферромагнитной цепью управления. АН РУз, Проблемы информатики и энергетика 1995. № 2.С.47–48.
3. Кадыров Т. М., Алимов Х. А., Файзиев М. М.-Исследование установившегося режима ферромагнитного удвоителя частоты, АН РУз, Проблемы информатики и энергетика 1997. № 3.С.29–33.
4. Кадыров Т. М.- Ферромагнитные цепи, обладающие широким падающим участком на амплитудной и фазовой характеристике. Известия ВУЗов, «Электромеханика», 1988, № 7,с 26–29.
