Настоящая статья посвящена созданию универсальной методике оценки надежности на основе применения метода статистических испытаний математической модели надежности аппаратуры СУ, отображающей реальную систему управления, в основу которого положен расчетно-экспериментальный статистический метод, использующий экспериментальные данные по областям работоспособности комплектующих элементов, в зависимости от формирования по ним потока неисправностей в аппаратуре СУ, и восхождения от них с помощью модели к оценке надежности СУ в целом.
Ключевые слова: надежность, система управления, летательные аппараты.
Система управления (СУ) летательных аппаратов проектируется как совокупность унифицированных функциональных трактов, объединённых интерфейсом и программой диспетчер в единую информационно-логическую систему. В зависимости от задач, предъявляемых к объекту управления и системе управления, набор функциональных трактов может изменяться и модифицироваться, не изменяя структуры СУ в целом. Такое представление СУ даёт возможность прогнозировать её характеристики надежности задолго до разработки конструкторской документации, изготовления и испытаний опытных образцов.
В качестве методического подхода к оценке надежности аппаратуры СУ летательных аппаратов выступают: модель, отображающая поток неисправностей в системе, обусловленный отказами комплектующих элементов и модель, отображающая свойство системы сохранять работоспособность при возникновения в ней неисправностей (для краткости первая-модель формирования потока неисправностей, вторая- модель работоспособности). Он базируется на использовании метода статистических испытаний и включает в себя ряд этапов, предусматривающих:
- описание системы управления как объекта оценки надежности;
- определение вероятности безотказной работы структурных звеньев;
- формирование потока неисправностей в СУ с использованием рекуррентного алгоритма оценки состояний системы;
- оценка работоспособности аппаратуры СУ при сформированной совокупности неисправностей в каждой реализации статистических испытаний;
- оценка надежности аппаратуры СУ по результатам статистического моделирования процесса эксплуатации.
Описание системы управления как объекта оценки надежности представляет собой комплекс алгоритмов, воспроизводящих процессы функционирования системы в реальных условиях эксплуатации с учётом особенностей её структурного построения.
Структурная модель СУ представляется либо в виде расчетно-функциональной структуры, или в виде структурно-логической схемы (по типу структурной схемы надежности). Как расчетно-функциональная структура, так и структурно-логическая схема строятся из структурных звеньев (СЗ) и учитывают примененные в системе виды резервирования (мажоритирования, дублирования и т. п.) при этом под структурным звеном понимается группа функционально связанных комплектующих элементов (КЭ) или функциональных узлов представляющих собой нерезервированный участок функциональной или структурно-логической схемы и не имеющих внутри себя точек встречи или разветвления обрабатываемой информации. Следствием такого способа формирования структурного звена является то, что сбой или отказ одного любого КЭ, входящего в структурное звено, приводит к его сбою или отказу. Примеры функциональной расчетной и логической схемы представлены на рисунках 1 и 2.
Конструктивно-компоновочная модель (ККМ) строится по иерархическому принципу — комплектующее систему электрорадиоизделие (ЭРИ) (в общем случае КЭ), плата, прибор, изделие в целом.
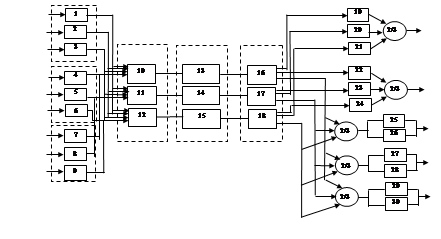
Рис. 1. Пример ФРС СУ для составления логических уравнений, определяющих условия работоспособности системы
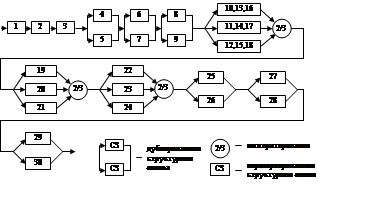
Рис. 2. Пример структурно-логической схемы системы
Начальной единицей расчёта надёжности системы управления летательных аппаратов является структурное звено. Характеристикой надёжности структурного звена служит вероятность безотказной работы за назначенное время. Так как структурное звено представляет собой совокупность последовательно соединённых между собой комплектующих элементов, то отказ одного любого элемента приведёт к отказу всего звена, а значит, вероятность сохранения его работоспособности определяется по формуле:
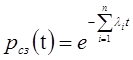 (1)
(1)
где 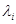 — интенсивность отказа i-го комплектующего элемента структурного звена;
— интенсивность отказа i-го комплектующего элемента структурного звена;
n — количество комплектующих элементов в структурном звене.
Вероятность отказа структурного звена будет равна
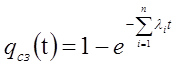 . (2)
. (2)
При систематическом значимом проявлении конструктивных и производственных отказов оценка достигнутой надежности СУ производится с учетом их влияния. При этом учет производственных и конструктивных дефектов может производиться следующими способами, определяемыми характером их проявления в системе.
Если появление конструктивных и производственных дефектов носит устойчивый статистический во времени характер, тогда учет этих отказов производится коэффициентом при λ-характеристиках ЭРИ тех структурных звеньев, в которых имели место данные дефекты
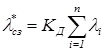 , (3)
, (3)
где 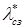 — интенсивность отказов структурного звена с учетом производственных и конструктивных дефектов;
— интенсивность отказов структурного звена с учетом производственных и конструктивных дефектов;
КД — коэффициент влияния производственных и конструктивных дефектов;
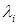 — суммарная интенсивность отказов i-гo типа ЭРИ;
— суммарная интенсивность отказов i-гo типа ЭРИ;
п — количество типов ЭРИ в структурном звене;
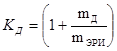 , (4)
, (4)
где mД, — количество отказов структурного звена (прибора, устройства) из-за производственных и конструктивных дефектов;
mЭРИ — количество отказов структурного звена из-за катастрофических отказов ЭРИ.
Вероятность безотказной работы структурного звена определяется по формуле:
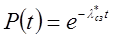 (5)
(5)
Формирование потока неисправностей в приборах системы управления с использованием рекуррентного алгоритма состояний системы представим следующим образом.
В связи с тем, что вероятность сохранения работоспособности СЗ существенно различны, вероятность состояний СУ с 0,1...n отказами СЗ не могут быть получены, например, по формулам биномиального распределения. Возможное применение метода перебора состояний системы неэффективно из-за большой размерности множества СЗ.
Выход из этой ситуации обеспечивается за счет применения следующего алгоритма определения вероятностей состояний СУ.
Пусть функционально-расчетная схема СУ состоит из N работоспособных СЗ. Определены вероятности сохранения работоспособности СЗ РСЗ1...РСЗn...РСЗ N. Тогда вероятность состояния СУ без отказов определится как
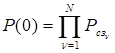 , (6)
, (6)
вероятность сохранения СУ с нарушением работоспособности любого одного СЗ:
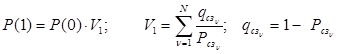 (7)
(7)
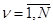 , причем для каждого j проводится цикл по n, а вероятность состояния СУ с j отказами (j=2,3...Ni) по рекуррентному соотношению
, причем для каждого j проводится цикл по n, а вероятность состояния СУ с j отказами (j=2,3...Ni) по рекуррентному соотношению
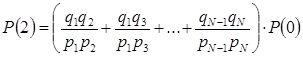 (8)
(8)
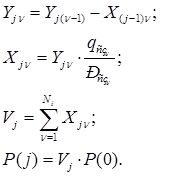 (9)
(9)
Начальные условия для рекуррентных вычислений
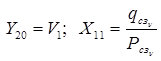 . (10)
. (10)
По полученным вероятностям состояния СУ по необратимым отказам КЭ определяется количество и номера неработоспособных СЗ в текущей реализации статистического моделирования. При проведении статистического моделирования процесс определения количества отказавших СЗ и их номеров осуществляется в следующей последовательности.
При вычислении вероятности состояния системы, как правило, учитывается не N — отказов, равное количеству СЗ, а n — отказов, при которых удовлетворяется условие
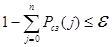 , (11)
, (11)
где 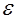 — наперед заданное положительное число, принимаемое на практике 0,0005. Поэтому для того, чтобы вероятности состояний системы с 0,1....n составляли полную группу несовместимых событий, производится их нормирование в соответствии с соотношением
— наперед заданное положительное число, принимаемое на практике 0,0005. Поэтому для того, чтобы вероятности состояний системы с 0,1....n составляли полную группу несовместимых событий, производится их нормирование в соответствии с соотношением
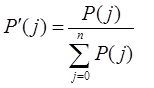 (12)
(12)
Далее, для определения количества отказавших СЗ вычисляется ряд вспомогательных величин:
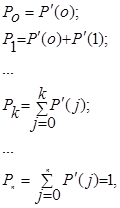 (13)
(13)
которые позволяют определить количество неработоспособных СЗ в l-ой реализации как результат выполнения первого в порядке следования соотношения
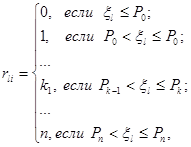 (14)
(14)
где xl — случайное число из равномерно распределенных на интервале (0, 1), выбранное в l-ой реализации.
При определении номеров отказавших СЗ используются вероятности отказов СЗ 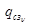 . При этом после выбора очередного номера, отказавшего СЗ, проводится нормирование вероятностей отказов оставшихся СЗ по формуле
. При этом после выбора очередного номера, отказавшего СЗ, проводится нормирование вероятностей отказов оставшихся СЗ по формуле
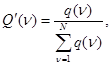 (15)
(15)
и вычисляются вспомогательные величины
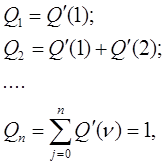 (16)
(16)
с помощью которых определяется номер отказавшего СЗ как результат выполнения первого в порядке следования соотношения
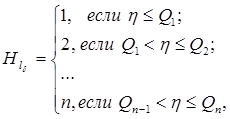 (17)
(17)
где 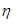 — случайное число из равномерно распределенных на интервале (0, 1).
— случайное число из равномерно распределенных на интервале (0, 1).
Таким образом, определяется совокупность возникающих отказов структурных звеньев для одного из участков временного графика процесса жизни системы. На каждом из последующих участков повторяются аналогичные операции, при этом в зависимости от принятой стратегии восстановления в процессе эксплуатации системы, отказы, возникшие на предыдущем участке, сохраняются или парируются.
Изложенный метод позволяет оценивать надежность аппаратуры системы управления летательных аппаратов с учетом формирования потока неисправностей с использованием рекуррентного алгоритма.







