На примере вязкоупругой оболочки рассмотрены задачи о колебаниях вязкоупругих трубопроводов с протекающей жидкостью. С помощью метода Бубнова — Галеркина математическая модель задачи сведена к исследованию системы обыкновенных интегро-дифференциальных уравнений, решаемых численным методом, основанном на использовании квадратурных формул.
Ключевые слова: математическая модель, вязкоупругость, интегро–дифференциальные уравнения, алгоритм, трубопровод
Чрезвычайно высокую роль в системе нефтегазовой отрасли промышленности играет трубопроводный транспорт. Он является основным и одним из дешевых видов транспорта нефти от мест добычи на нефтеперерабатывающие заводы и экспорт. Надежность в эксплуатации, экономичность, высокая эффективность и простота в управлении — все это преимущество трубопроводного транспорта перед другими видами транспортировками.
Современный тонкостенный трубопровод большого диаметра с рабочим внутренним давлением более 10 МПа представляет собой не обычный стержень или балку, а тонкую цилиндрическую оболочку с деформируемым контуром поперечного сечения. Поэтому для расчета такого трубопровода следует применять не традиционную стержневую теорию, а теории тонких оболочек с учетом взаимодействия конструкции с внутренней и внешней средой [1, 2].
В настоящее время нефтегазовая промышленность мира сталкивается с проблемой ремонта, реконструкции и восстановления трубопроводов. Один из путей решения данной проблемы — применение современных, ресурсосберегающих, экологически безопасных технологий, к которым можно отнести использование неметаллических, в частности труб из полимерных композиционных материалов [3–5].
Целью данный работы является создание математической модели, численный алгоритм и компьютерной программы для решения задачи о свободных колебаниях вязкоупругих тонкостенных трубопроводов большого диаметра на базе теории оболочек.
Рассмотрим поведение тонкой круговой вязкоупругой цилиндрической оболочки, внутри которой с постоянной скоростью U движется идеальная жидкость. Примем здесь вариант линеаризованный теории оболочек, считая прогибы малыми по сравнению с толщиной. Тогда, пренебрегая нелинейными составляющими в уравнения Маргерра [6, 7] и пологая 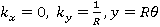 , получим следующие уравнения относительно перемещений
, получим следующие уравнения относительно перемещений 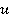 ,
, 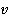 и
и 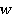 с учетом вязкоупругих свойств материала конструкций:
с учетом вязкоупругих свойств материала конструкций:
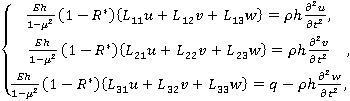 (1)
(1)
где 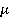 — коэффициент Пуассона,
— коэффициент Пуассона, 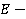 модуль упругости,
модуль упругости, 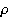 — плотность материала; h — толщина оболочки;
— плотность материала; h — толщина оболочки; 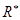 – интегральный оператор вида:
– интегральный оператор вида: 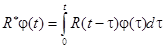 ;
; 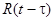 — ядро релаксации;
— ядро релаксации;
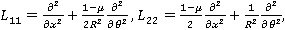
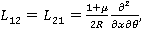
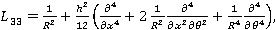
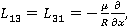
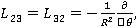
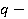 давление жидкости на стенку оболочки:
давление жидкости на стенку оболочки:
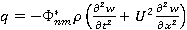 ; (2)
; (2)
где 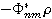 — присоединенная масса жидкости;
— присоединенная масса жидкости; 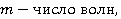 образующихся по окружности,
образующихся по окружности, 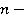 волновой число или постоянной распространения фазы.
волновой число или постоянной распространения фазы.
Введем безразмерные параметры
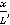
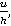
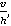
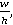
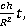
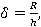
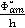 ,
, 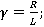
здесь 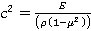 . Тогда вместо (1) получим
. Тогда вместо (1) получим
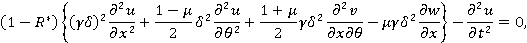
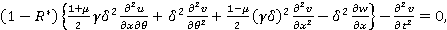 (3)
(3)
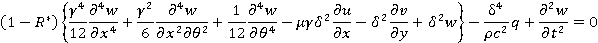
Будем искать приближенное решение системы (1) в виде:
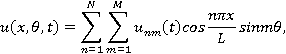
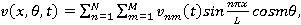 (4)
(4)
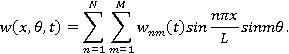
Подставляя (4) в систему (1) и применяя метод Бубнова — Галёркина, получим систему интегродифференциальных уравнений (ИДУ):
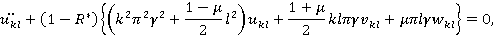
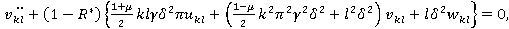 (5)
(5)
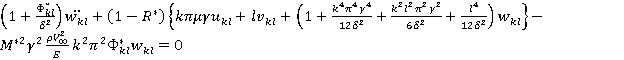 .
.
unm(0)=u0nm, 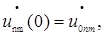 vnm(0)=v0nm,
vnm(0)=v0nm, 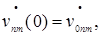 wnm(0)=w0nm,
wnm(0)=w0nm, 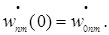
Далее к системе (5), описывающей линейные задачи о колебаниях вязкоупругих трубопроводов, применен численный метод [8,10]. Следующим этапом численного метода является регуляризация системы ИДУ (5) с сингулярными ядрами. С помощью замены переменных
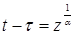 ,
, 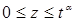 (0<α<1) (6)
(0<α<1) (6)
интеграл при ядре Колтунова-Ржаницына с особенностью следующего вида
А (7)
(7)
принимает вид
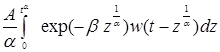 . (8)
. (8)
Заметим, что после замены переменных подынтегральная функция относительно z становится регулярной. Полагая затем t=ti, ti=iDt, i=1,2,… (Dt=const — шаг интерполяции) и заменяя интегралы некоторыми квадратурными формулами (в частности по формуле трапеции), имеем
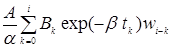 (9)
(9)
где коэффициенты 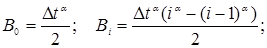
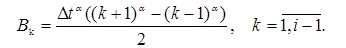
На основе этого метода описан алгоритм численного решения системы (5). Интегрируя систему (5) два раза по t, можно записать ее в интегральной форме и с помощью рационального преобразования исключим сингулярные особенности интегрального оператора R*. Затем, полагая t=ti, ti=ih, i=1,2,… (h=const) и заменяя интегралы квадратурными формулами трапеций для вычисления uikl=ukl(ti), vikl=vkl(ti) и wikl=wkl(ti), получим следующие рекуррентные формулы для ядра Колтунова — Ржаницына 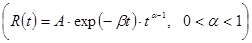 :
:
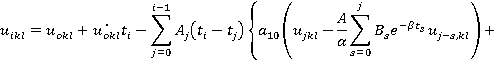
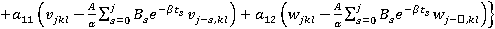 ,
,
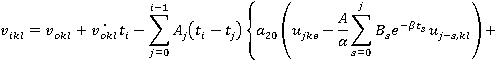
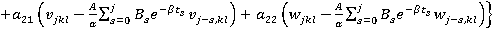 , (10)
, (10)
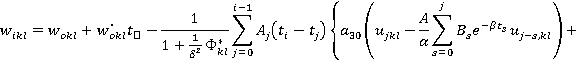
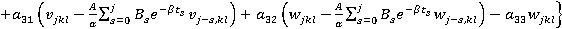 ,
,
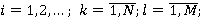
где 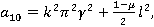
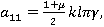
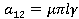 ,
,
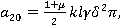
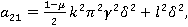
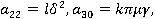
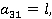
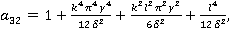
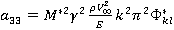 .
.
Здесь 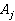 ,
, 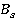 — числовые коэффициенты применительно к квадратурным формулам трапеции [8–10].
— числовые коэффициенты применительно к квадратурным формулам трапеции [8–10].
Благодаря предложенному подходу в алгоритме для численного решения задачи в формуле (10) множитель 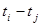 при j = i принимает нулевое значение, т. е. последнее слагаемое суммы равно нулю. Поэтому суммирование осуществляется от нуля до i-1 (
при j = i принимает нулевое значение, т. е. последнее слагаемое суммы равно нулю. Поэтому суммирование осуществляется от нуля до i-1 (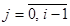 ).
).
Таким образом, согласно численному методу относительно неизвестных, получим систему линейных алгебраических уравнений. Для решения системы используется метод Гаусса. На основе разработанного алгоритма создан пакет прикладных программ на языке «Delphi».
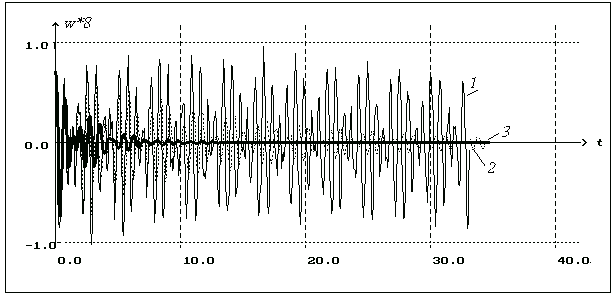
Рис. 1. Зависимость перемещений w от времени t для различных значений параметра вязкости: 1- А=0,001; 2 — А=0,02; 3 — А=0,1
На рисунке приведены зависимости прогиба w от времени t для различных значений реологического параметра А. Из этого рисунка видно, что с увеличением параметра А амплитуда и частота колебаний оболочек уменьшаются.
Необходимо отметить, что алгоритм предлагаемого метода позволяет детально исследовать влияние реологических параметров на характер колебательной устойчивости вязкоупругих трубопроводов, в частности, при исследовании свободных колебаний трубопроводов на базе теории идеально-упругих оболочек.
Литература:
1. Соколов В. Г. Колебания, статическая и динамическая устойчивость трубопроводов большого диаметра // Автореферат дис.… док. технических наук: 05.23.17. Санкт-Петербург, 2012. 36 с.
2. Ефимов А. А. Колебания и динамическая устойчивость глубоководных нефтегазопроводов //Автореферат дис.... канд. техн. наук: 05.23.17. Тюмень, 2009.
3. Аношкин А. Н., Зуйко В. Ю., Иванов С. Г. Расчет напряженно-деформированного состояния и прогнозирование прочности полимерных армированных труб газового назначения // Вестник СамГУ. Естественнонаучная серия. 2007. № 6(56). С.419–426.
4. Ягубов Э. З. Использование высокопрочных стеклопластиковых труб в нефтянной промышленности // Нефтянное хозяйство. — 2001. — № 6. — С.68–70.
5. Ягубов Э. З., Цхадая Н. Д., Якубов З. Х. Многоканалные трубопроводы для транспортировк нефтегазовых сред и востановление изношенных нефтегазопроводов // Научные труды. — 2013. — № 1. — С. 57–63.
6. Вольмир А. С. Оболочки в потоке жидкости и газа. Задачи гидроупругости. — М.: Наука. 1979. — 320 с.
7. Григолюк Э. И., Мамай В. И. Нелинейное деформирование тонкостенных конструкций. — М.: Наука. Физматлит, 1997. — 272 с.
8. Бадалов Ф. Б. Методы решения интегральных и интегро-дифференциальных уравнений наследственной теории вязкоупругости. Ташкент: Мехнат, 1987. 269 с.
9. Худаяров Б. А., Бандурин Н. Г. Нелинейный флаттер вязкоупругих отротропных цилиндрических панелей // Математическое моделирование. РАН. 2005. Том 17, № 10. — С. 79–86.
10. Бадалов Ф. Б., Худаяров Б. А., Абдукаримов А. Исследование влияния ядра наследственности на решение линейных и нелинейных динамических задач наследственно-деформируемых систем // Проблемы машиностроения и надежности машин. Российская академия наук. — 2007. — № 4. — С. 107–110.







