Статья интересна будет проектировщикам, занимающимся расчетами на прочность, студентам, изучающим сопротивление материалов, а также преподавателям технических вузов. При расчете стержня переменного поперечного сечения, работающего на сжатие и изгиб, возникает необходимость определить прочность стержня. К таким расчетным схемам можно, например, привести буксировочные водила для летательных аппаратов. Решение подобных задач унифицировано можно решить с помощью предложенной методики. В ней имеется вывод формулы и предложены примеры использования выведенной формулы.
Расчёт ведется по следующей схеме:
- определяем критическую сжимающую нагрузку для стержня переменного сечения;
- определяем величину 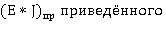 эквивалентного стержня постоянного сечения. Критерием эквивалентности принимаем равенство критической разрушающей нагрузки как для стержня переменного, так и постоянного сечений
эквивалентного стержня постоянного сечения. Критерием эквивалентности принимаем равенство критической разрушающей нагрузки как для стержня переменного, так и постоянного сечений
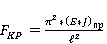 (1)
(1)
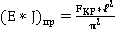 (2)
(2)
—нагружаем эквивалентный стержень постоянного сечения нагрузкой стержня переменного сечения и находим изгибающие моменты, которые считаем, верны и для стержня переменного сечения.
При выводе формул используются обозначения-
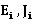 -модули упругости материалов и моменты инерции участков,
-модули упругости материалов и моменты инерции участков,
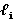 — длины участков.
— длины участков.
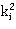 =
=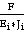 — коэффициент
— коэффициент
 Формулы выводили на основе теории малых деформаций, составляя дифференциальные уравнения упругой линии стержня на каждом из участков.
Формулы выводили на основе теории малых деформаций, составляя дифференциальные уравнения упругой линии стержня на каждом из участков.
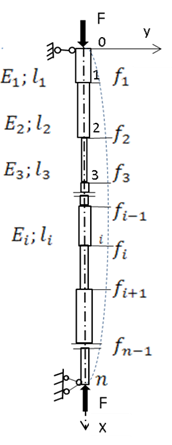
Рис.1. Расчётная схема
Вывод формулы для определения 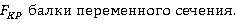
Дифференциальные уравнения упругих линий участков.
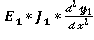 = — F
= — F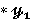
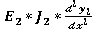 = — F
= — F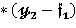
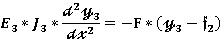
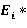
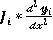 = -F
= -F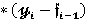
Решения дифференциальных уравнений.
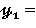
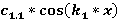 +
+ 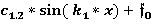
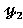 =
= 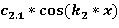 +
+ 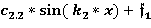
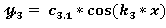 +
+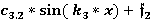
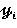 =
= 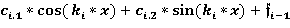
Постоянные интегрирования найдём из следующих условий
Берём два участка 𝒊 и (𝒊+1).
Участок 𝒊
При X =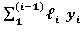 =
= 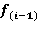
При X = 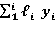 =
=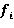
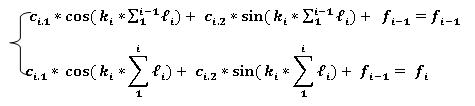
Решение системы из двух уравнений
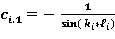 *(
*(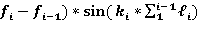
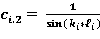 *(
*(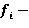
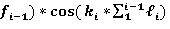
Участок (𝒊+1)
При X = 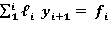
При X =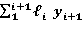 =
= 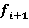
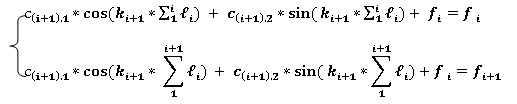
Решение системы из двух уравнений
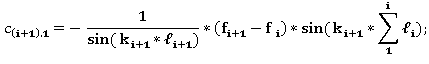
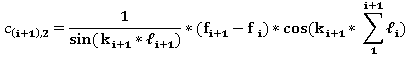
Так как два участка изогнутой оси имеют одну и ту же касательную, при X=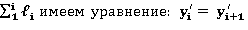 или
или
—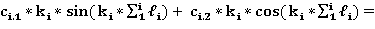
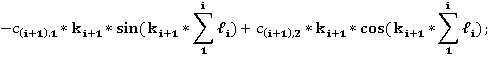
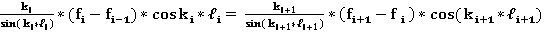 (3)
(3)
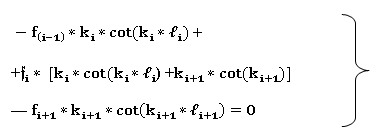 (4)
(4)
Подставляя уравнение (4) для каждого стыка стержня получим систему уравнений для определения  Определение Fкр для следующих расчётных схем с использованием формулы (4).
Определение Fкр для следующих расчётных схем с использованием формулы (4).
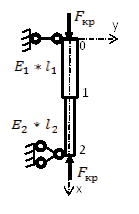
Рис. 2. Расчетная схема
Для стыка 1 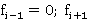 =0, и по формуле (4) п
=0, и по формуле (4) п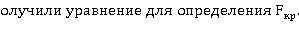
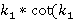 *
*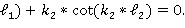 (5)
(5)
Для расчетной схемы Рис.3, используя формулу 4 для стыков 1 и 2, получим систему из двух уравнений.
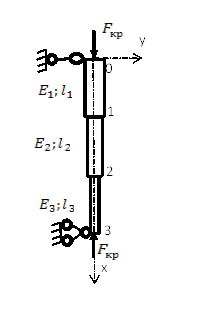
Рис. 3. Расчетная схема
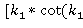 *
*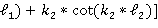 *
*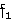 -
- 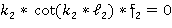
—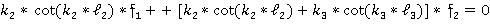
Приравнивая определитель системы уравнений к 0, имеем уравнение для определения 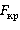 .
.
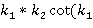 *
*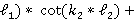
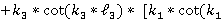 *
*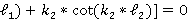 (6)
(6)
Решая трансцендентные уравнения определяем Fкр.
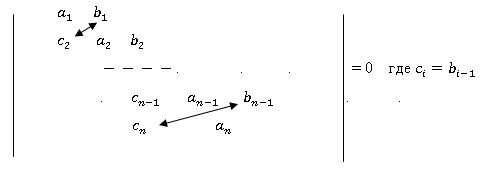
Общее решение для определения Fкр
Якобиевая матрица, коэффициенты которой определяются
подстановкой уравнения (4) для каждого стыка балки.
Алгоритм решения трансцендентного уравнения методами: табуляции, деления отрезка пополам приведен в Приложении № 1 на языке Visual Basic 6.
Приложение № 1
Private Sub Command1_Click()
e = 0.005
maxi = 10
a = Val(InputBox(«vvedite granicy otreska a: "))
b = Val(InputBox(«vvedite granicy otreska b: "))
Call Tabulation(a, b, 2.5)
For I = 1 To maxi
fa = f(a)
fb = f(b)
If fa * fb < 0 Then
x = (a + b) / 2
fx = f(x)
Debug.Print " iteraciya= " + CStr(I)
Debug.Print " x= " + Format(x, "00.00")
Debug.Print " (f(x))= " + Format(fx, "00.0000")
If Abs(fx) < e Then
Debug.Print " reschenie naideno, x= " + CStr(x)
Debug.Print " za " + CStr(I) + " iteraciya!!!"
solution = True
Exit Sub
Else
If fa * fx < 0 Then
b = x
End If
If fx * fb < 0 Then
a = x
End If
End If
Else
Debug.Print " iteraciya = " + CStr(I)
Debug.Print ": f(a)= " + Format(fa, "00.0000")
Debug.Print ": f(b)= " + Format(fb, "00.0000")
Debug.Print " otrezok [a,b] vibran neydachno!!!"
Exit Sub
End If
Next I
If Not solution Then Debug.Print «reschenie ne naideno za», maxi, «iteraciya»
End Sub
Function f(x)
f = 1.57 / Tan(0.008 * x) + 1 / Tan(0.009 * x)
End Function
Sub Tabulation(a, b, abstep)
Debug.Print "---tabylyaciya fynkcii---"
For x = a To b Step abstep
Debug.Print «x= " + Format(x, "00.00") + ": " + «f(x)= " + Format(f(x), "00.0000")
Next x
Debug.Print "-----------------------"
End Sub
Литература:
1. Тимошенко С. П. Сопротивление материалов. Т.2.







