Математика — это наука не только о пространственных формах и количественных соотношениях, математика — это универсальный язык природы, так как явления и процессы в природе описываются определенными математическими закономерностями. В то же время нет ни одной области человеческой деятельности, где бы не использовались математические методы. Исторически сложилось, что математика находилась у истоков развития любой науки, наряду с философией. Предметом изучения последней являются методы познания мира.
Данный курс посвящен одному из методов познания — методу математического моделирования. Суть его заключается в создании модели некоторого явления с целью дальнейшего изучения полученной модели. При этом модель представляет собой «приближенное описание какого-либо класса явлений внешнего мира, выраженное с помощью математической символики».
Новизна и оригинальность данной программы заключается в том, что учащиеся применяют метод математического моделирования в ситуациях, отличных от тех, которые им встречаются на уроках математики. Подобранные задачи позволяют осуществлять межпредметные связи математики и других областей, таких как физика, химия, биология, экономика, архитектура, музыка. Программа подразумевает использование метода активного обучения: каждая математическая модель изучается через решение серии задач прикладного и практического характера (количество часов, отведенных на теорию, значительно меньше часов практики). Система практико-ориентированных задач направлена на выявление склонностей и способностей учащихся, т. к. представлена широким спектром предметных областей, а также учитывает уровневую дифференциацию обучения.
Наконец, обучение решению практико-ориентированных задач предполагает применение современных информационных технологий.
Актуальность программы заключается в том, что учащиеся приобретают универсальный (метапредметный) навык математического моделирования, метода который применяется при решении задач из разных областей знания.
Данный курс способствует также реализации прикладной направленности обучения математике, необходимость которой обусловлена и с точки зрения психологии. Выпускник основной школы оказывается перед выбором профиля дальнейшего обучения. Избежать ошибок в выборе профиля возможно в том случае, если учащийся будет хорошо проинформирован о различных профессиональных областях деятельности, а также реально оценивать свои возможности и способности к конкретной деятельности, осознавать свои потребности, склонности и интересы. Поэтому данная программа будет полезна для организации предпрофильной дифференциации обучения математике.
Наконец, без организации прикладного характера обучения знания, получаемые учащимися, остаются фрагментарными, разобщенными, оторванными от практики и жизни.
Цель программы: развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения опыта математического моделирования.
Для достижения поставленной цели программы необходимо решение следующих задач учебно-воспитательного процесса:
Обучающие задачи:
- формирование представления о методе математического моделирования явлений и процессов;
- развитие умения видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
- развитие умения находить в различных источниках информацию, необходимую для решения математической проблемы; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
- развитие умения понимать и использовать математические средства наглядности (графики, диаграммы, схемы и т. д.);
- развитие умения планировать и осуществлять деятельность, направленную на решение задач исследовательского характера
Развивающие задачи:
- развитие логического и критического мышления, культуры речи, способности к умственному эксперименту
- развитие навыков исследовательской деятельности
- воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;
- формирование качеств мышления, необходимых для адаптации в современном информационном обществе
Воспитательные задачи:
- формирование представления о единой картине мира на основе понимания того, что математика является универсальным языком природы и науки, а математические методы используются в различных областях деятельности человека.
- развитие умения контролировать процесс и результат учебной математической деятельности;
- развитие навыков работы сотрудничества в коллективе;
- формирование адекватной оценки своих способностей к математике
- выявление направленности личности (познавательных и профессиональных интересов) средствами предмета математики.
Направленность программы: естественнонаучная
Вид деятельности: творческие и исследовательские предметные и межпредметные проекты.
Программа рассчитана на 3 года и предназначена для работы во внеурочное время с учащимися, интересующихся математикой, желающие приобрести навыки исследовательской и творческой работы.
Занятия проводятся в группах не более 15 человек. Такое количество детей в группе является оптимальным, позволяя осуществлять индивидуальный и дифференцированный подход в процессе обучения.
Режим занятий: 1 раз в неделю по 45 минут.
Возраст детей 12–15 лет.
Прогнозируемые результаты и способы их проверки
В результате занятий по программе «Сквозь призму науки» приобретают:
- навыки моделирования, преобразования модели с целью выявления общих законов, определяющих данную предметную область;
- умение выдвигать гипотезы;
- умение работать с математическим текстом (структурирование, извлечение необходимой информации);
- умение выполненять устных, письменных, инструментальных вычислений; проведение несложных практических расчетов с использованием при необходимости справочных материалов, калькулятора, компьютера;
- умение пользоваться математическими формулами и самостоятельно составлять формулы зависимостей между величинами на основе обобщения частных случаев и эксперимента;
- навык применения графического представления для решения и исследования уравнений, неравенств, систем; применения математических знаний и умений для решения задач из математики, смежных предметов, практики;
- навык построения графиков функций, использования функционально-графического представления для описания и анализа учебных математических задач и реальных зависимостей;
- умение использования основных способов представления и анализа статистических данных; решение задач на нахождение частоты и вероятности случайных событий;
- умения применять изученные понятия, результаты и методы при решении задач из различных разделов курса, в том числе задач, не сводящихся к непосредственному применению известных алгоритмов;
- умение точно и грамотно излагать мысль в устной и письменной речи, применять математическую терминологию и символику; обосновывать суждения, проводить классификацию, доказательство математического утверждения.
К концу 1-го года обучения обучающиеся должны:
- уметь создавать модели простейших процессов;
- выполнять устные, письменные, инструментальные вычисления; проводить несложные практические расчетов с использованием при необходимости справочных материалов, калькулятора, компьютера;
- умение пользоваться математическими формулами;
- применять графическое представление для решения задач из математики, смежных предметов, практики, связанных с исследованием линейного уравнения, неравенств, систем
- уметь решать простейшие статистические задачи.
К концу 2-го года обучения обучающиеся должны:
- моделировать, преобразовывать модели с целью выявления общих законов, определяющих данную предметную область
- уметь не только пользоваться математическими формулами, но и самостоятельно составлять формулы зависимостей между величинами
- строить графики изученных функций, использовать функционально-графическое представления для описания и анализа учебных математических задач и реальных зависимостей;
- использовать основные способы представления и анализа статистических данных
К концу 3-го года обучения обучающиеся должны:
- уметь моделировать реальный процесс, проводить изучение модели;
- выдвигать гипотезы и их обоснование;
- умение работать с математическим текстом (структурирование, извлечение необходимой информации);
- выполнять вычисления; проводить практические расчеты с использованием калькулятора, компьютера;
- умение составлять формулы зависимостей между величинами на основе обобщения частных случаев и эксперимента;
- использовать функционально-графический метод для описания и анализа учебных математических задач и реальных зависимостей;
- использовать основные способы представления и анализа статистических данных; решать задач на нахождение частоты и вероятности случайных событий;
- уметь производить несложные построения с помощью циркуля и линейки.
- применять метод моделирования при решении задач из различных предметных областей, в том числе задач, не сводящихся к непосредственному применению известных алгоритмов;
- уметь точно и грамотно излагать мысли в устной и письменной речи, применять математическую терминологию и символику; обосновывать суждения, проводить доказательство утверждения.
Результативность работы по данной программе оценивается в разных формах:
1. Выставка творческих работ (модели, оформление стендовых докладов).
2. Защита проектных работ на итоговом занятии: математической конференции «Я моделирую…».
3. Участие в ежегодной школьной конференции «Истоки», межшкольных и окружных конференциях.
4. По результатам анкетирования учащихся на предмет профессионального самоопределения
Учебно-тематический план занятий
1-й год обучения
Количество учащихся — не более 15 человек
Возраст — 12–13 лет (7 классы)
Количество занятий: 1 час в неделю
Количество часов за учебный год — 28
|
№ п/п |
Темы занятий |
Общее кол-во часов |
Часы теории |
Часы практики |
|
1 |
Вводное занятие. |
1 |
1 |
0 |
|
2 |
Измерения. |
1 |
0,5 |
0,5 |
|
3 |
Модель «Проценты ". Процентные расчеты в жизненных ситуациях. |
7 |
1 |
6 |
|
4 |
Математическая модель «Отношения и пропорции». Золотое сечение и гармония форм природы и искусства |
9 |
2 |
7 |
|
5 |
Математическая модель «Функция» |
3 |
0,5 |
2,5 |
|
6 |
Математическая модель «Линейное уравнение с одной переменной " |
3 |
0,5 |
2,5 |
|
7 |
Математическая модель «Система линейных уравнений» |
3 |
0,5 |
2,5 |
|
8 |
Итоговое занятие.
|
1 |
0 |
1 |
|
|
Итого |
28 |
7 |
21 |
Содержание занятий
1. Вводное занятие (1 час)
1.1. Метод математического моделирования. Виды моделей.
1.2. Этапы решения практико-ориентированных задач.
1.3. Техника безопасности работы за компьютером.
2. Измерения (1 час).
2.1. Точность и погрешность измерений. Абсолютная и относительная погрешности. Причина возможных ошибок в измерениях.
2.2. Практическая работа. Определение цены деления приборов: термометра, психрометра, линейки, амперметра, вольтметра, напольных весов.
2.3. Практическая работа «Моя средняя скорость движения»
3. Модель «Проценты». Процентные расчеты в жизненных ситуациях
1. (7 часов).
3.1. Основные понятия, связанные с процентами. Простые и сложные проценты. Проценты как математическая модель решения практических задач.
3.2. Домашние заготовки. Создание растворов требуемой концентрации для засолки овощей, приготовления компотов и варенья, расчет количества продуктов по рецепту
2. Проект «Мой кулинарный шедевр»
3.3. Выгодная покупка. Распродажа, скидки.
3.4. Выбираем золотые и серебряные украшения. Что означает проба на ювелирных украшениях?
Доклад " Почему золото называется червонным?" Из истории ювелирного дела. Получение золота. Задачи на смеси и сплавы, концентрацию.
Практическая работа. «Готовлю раствор»
3.5. Коммунальные платежи. Тарифы, штрафы.
1.1. Практическая работа. «Расчет оплаты коммунальных платежей своей семьи».
3.6. Что значит жить «на проценты»? Банковские операции. Стратегия ликвидности, стратегия доходности, ценные вклады, государственные краткосрочные облигации. Задачи на процентный прирост и вычисление “сложных процентов”
1.2. Практическая работа «Как сделать выгодный вклад?"
3.7. Процентные расчеты в физике и географии, метеорологии, медицине, фармацевтике и социологии (прогнозирование демографической ситуации в стране, статистические расчеты).
4. Математическая модель «Отношения и пропорции». Золотое сечение и гармония форм природы и искусства (9 часов)
4.1. Золотое сечение. Основные понятия. Математическое определение «золотого сечения». История золотого сечения. Числа Фибоначчи.
4.2. Золотое сечение в математике. «Золотой» прямоугольник, треугольник, пентаграмма.
Проектная работа. «Строим «золотые» фигуры»
4.3. Золотое сечение в природе. Спираль Архимеда.
Практическая работа. Определение «золотого сечения» в пропорциях куриного яйца, ветки клена.
Практическая работа. «Золотое сечение» в расположении семян подсолнечника, шишек сосны.
Практическая работа. «Ищем спираль Архимеда»(на примере природного материала морских и речных ракушек, паутины)
4.4. Пропорции человеческого тела.
Проектная работа «Золотое сечение в строении моего тела».
4.5. Золотое сечение в живописи
Исследовательская работа " Изучаем репродукцию картины «Мона Лиза» Леонардо да Винчи»
Исследовательская работа «Изучаем репродукцию картины «Тайная вечеря», «Рождение Венеры»
Исследовательская работа «Изучаем репродукцию картины» Афинская школа " Рафаэля Санти"
Исследовательская работа. Золотое сечение в работах Андрея Рублева (на примере репродукции иконы»Троица»)
4.6. Золотое сечение в музыке
Исследовательская работа " Главные золотые сечения Хроматической фантазии И. С. Баха». Исследуем произведения Л. Бетховена и Ф. Шопена.
4.7. Золотое сечение в литературе. Золотое сечение в произведениях М. Ю. Лермонтова, А. С. Пушкина
Проектная работа «Сочиняю стихи»...
4.8. Золотое сечение в архитектуре. Архитектура древности. Парфенон. Египетские пирамиды. Нотр-Дам де Пари. Церковь Покрова на Нерли.
Проект. «Пропорции церкви Вознесения в Колменском»
Проект. «Золотое сечение Храма Василия Блаженного»
Проект. Фотоальбом. Золотое сечение в архитектуре Москвы.
4.9. Коллективный проект «Хочу быть картографом» (изучение пришкольного участка, выполнение измерений и создание карты участка в заданном масштабе).
5. Математическая модель «Функция»(3 часа)
5.1. Понятие функции в математике. График функции. Линейная функция и ее график. Моделирование процессов на компьютере с помощью программ — графопостроителей.
5.2. Функции в экономике. Функция спроса и предложения. Решение задач.
5.3. Функциональные зависимости в физике, химии. Решение задач.
5.4. Графическое решение практико-ориентированных задач с использованием компьютера.
6. Математическая модель «Линейное уравнение с одной переменной"(3 часа)
6.1. Основные понятия, связанные с линейным уравнением. Линейное уравнение с одной переменной как математическая модель решения задач.
6.2. Линейное уравнение в задачах экономического содержания.
Производство, рентабельность и производительность труда. Расчет выгоды от произведенной продукции, понятие чистой прибыли.
Спрос и предложение.
6.3. Линейное уравнение в задачах по физике на равномерное прямолинейное движение тел. Использование компьютерных средств для решения линейных уравнений.
7. Математическая модель «Система линейных уравнений» (3 часа)
7.1. Система линейных уравнений как математическая модель решения задач из области экономики (нахождение рыночного равновесия, определение рентабельности, оптимальной стоимости товара, задачи на совместную работу).
7.2. Задачи физического характера (определение координат места и времени встречи тел, движущихся прямолинейно и равномерно и др.)
8. Итоговое занятие (1 час). Представление макетов, моделей, защита проектных и исследовательских работ, представление стендовых докладов.
Учебно-тематический план занятий
2-й год обучения
Количество учащихся — не более 15 человек
Возраст — 13–14 лет (8 классы)
Количество занятий: 1 час в неделю
Количество часов за учебный год — 28
|
№ п/п |
Темы занятий |
Общее кол-во часов |
Часы теории |
Часы практики |
|
1. |
Вводное занятие |
1 |
1 |
0 |
|
2. |
Симметрия — основополагающий принцип устройства мира |
5 |
1 |
4 |
|
3. |
Геометрия живописи |
5 |
2 |
3 |
|
4. |
Математическая модель «Функция |
3 |
1 |
2 |
|
5. |
Математические модели «Квадратное уравнение» и «Квадратичная функция» |
4 |
1 |
3 |
|
6. |
Использование методов математической статистики при решении практико-ориентированных задач |
4 |
2 |
2 |
|
7. |
Модель «Графы» |
5 |
2 |
3 |
|
8. |
Итоговое занятие |
1 |
0 |
1 |
|
9. |
Итого |
28 |
10 |
18 |
Содержание занятий
1. Вводное занятие (1 час)
1.1. Компьютерное моделирование. Знакомство с программами — графопостроителями (1 час).
1.2. Инструктаж по технике безопасности работы с компьютером.
2. Симметрия — основополагающий принцип устройства мира (5 часов)
2.1. Симметрия в математике. Понятие симметрии. Виды симметрий. Симметрия геометрических фигур.
Практическая работа: «Строим фигуру, симметричную данной с использованием циркуля и линейки»
Симметрия правильных многогранников. Платоновы тела: тетраэдр («огонь»), гексаэдр («земля»), октаэдр (воздух), додекаэдр («вселенная»), икосаэдр (вода). Космический кубок Кеплера.
Проектная работа. «Платоновы тела своими руками»
Проектная работа «Воссоздаем модель космического кубка Кеплера»
2.2. Симметрия в природе. Зеркальная симметрия. Симметрия снежинки. Симметрия бабочки. Отражение в воде — единственный пример горизонтальной симметрии в природе.
Симметрия простейших микроорганизмов радиолярий. Симметрия в строении тела человека.
Лабораторная работа с использованием микроскопа «Симметрия простейших».
2.3. Симметрия в архитектуре. Московский Кремль. Симметрия и асимметрия в здании храма Василия Блаженного.
2.4. Симметрия в декоративно-прикладном искусстве. Розетки. Орнаменты.
Практическая работа «Конструируя красоту орнамента»
Паркет как вид орнамента и математическая задача о «замощении» плоскости.
Доклады:
- Виды линейных орнаментов (бордюров)
- Симметрия орнаментальных решеток
- Паркет из правильных многоугольников
- Задачи на построение афрасиабских панелей
- Художественные особенности национальных орнаментов
- Построение розеток и задачи деления окружности на части
Матрешки как пример симметрии подобия.
2.5. Симметрия в поэзии и музыке. Сочетание симметрии и асимметрии в философии М.Эшера.
3. Геометрия живописи (4 часа)
3.1. Понятие начертательной геометрии. Проекции. Виды проекций. Ортогональные, аксонометрические и центральные проекции. Перспектива: прямая и обратная.
3.2. Из истории развития живописи. Ортогональная живопись древнего Египта. Параллельная живопись средневекового Китая и Японии. Линейная перспектива Возрождения. Приспособление Дюрера. Обратная перспектива живописи древней Руси.
3.3. 3.4. Исследовательская работа. «Перспективный анализ репродукций: «Троицы» Андрея Рублева, миниатюры «Дионисий Младший», репродукции «Церковь Св.Елены» В.Поленова ".
Проектная работа. Изображение предмета в перспективе с использованием прибора Дюрера. (Прибор Дюрера готовят учащиеся самостоятельно).
Проектная работа. Построение перспективы интерьера комнаты способом архитекторов.
Проектная работа «Создавая картину»(учащиеся изображают предметы или композицию предметов по их выбору с учетом законов геометрической перспективы: изменения размеров предметов при удалении, угла обзора, падения тени).
4. Математическая модель «Функция 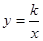 » (3 часа)
» (3 часа)
4.1. Функция обратной пропорциональности и ее график.
4.2. Что объединяет закон Гука и второй закон Ньютона?
1.1. Практическая работа: «Математика» в учебниках физики, химии, географии, биологии». Отбор задач для модели обратной пропорциональности.
4.3 Графическое решение задач. Применение компьютерного моделирования для решения задач. Проведение лабораторной работы с использованием компьютерных программ
5. Математические модели «Квадратное уравнение» и «Квадратичная функция» (4 часа)
- Экономические задачи, связанные с производством, расчетом прибыли от реализации товара, определение оптимальной цены.
- Задачи физического характера на прямолинейное равноускоренное движение, равноускоренное движение по окружности.
- Задача о вычислении глубины колодца с помощью подручных средств. Задачи, связанные с ростом численности популяций в биологии.
Практическая работа «Исследование реальных процессов с помощью графиков функций» (с использованием программы АвтоГраф)
6. Использование методов математической статистики при решении практико-ориентированных задач (4 часа)
- Таблицы. Поиск информации, представленной таблицей, графиком.
Практическая работа
«Один день заведующего складом»,
«Оптимизация работы библиотеки»
(Организация поиска данных в электронных таблицах Excel»).
- Диаграммы. Виды диаграмм.
Практическая работа. Построение диаграмм по заданным в условии задачи значениям с использованием компьютера.
- Основные понятия описательной статистики. Среднее значение. Медиана. Размах. Отклонения и дисперсия. Свойства среднего арифметического и дисперсии. Решение задач прикладного и практического характера на вычисление среднего значения, медианы, размаха, дисперсии.
- Лабораторная работа с применением программы «Интерактивная статистика»
7. Модель «Графы» (5 часов)
- Основные понятия теории графов. Деревья и их свойства.
- Задача о личном колодце или рассорившихся соседях.
- Задача о кенигсбергских мостах.
- Задача о четырех красках.
- Задачи о нахождении кратчайшего пути (на оптимизацию). Использование компьютера при решении задач на оптимизацию.
8. Итоговое занятие (1 час). Представление проектных и исследовательских работ.
Учебно-тематический план занятий
3-й год обучения
Количество учащихся — 10–15 человек
Возраст — 14–15 лет (9 классы)
Количество занятий: 1 час в неделю
Количество часов за учебный год — 28
|
№ п/п |
Темы занятий |
Общее кол-во часов |
Часы теории |
Часы практики |
|
1. |
Вводное занятие |
1 |
1 |
- |
|
2. |
Математическая логика |
6 |
2 |
4 |
|
3. |
Математическая модель «Степенная функция» |
2 |
0,5 |
1,5 |
|
4. |
Математические модели «Система уравнений», «система неравенств» |
2 |
0,5 |
1,5 |
|
5. |
Элементы теории вероятностей и математической статистики |
3 |
1 |
2 |
|
6. |
Кривые в природе и технике |
6 |
3 |
3 |
|
7. |
Геометрические построения и измерения на местности |
4 |
2 |
2 |
|
8. |
Фракталы: наука и искусство XXI века |
3 |
1 |
2 |
|
9. |
Итоговое занятие |
1 |
0 |
1 |
|
|
Итого |
28 |
11 |
17 |
Содержание занятий
1. Вводное занятие (1 час)
1.1. Математическое моделирование как метод познания.
1.2. Техника безопасности работы за компьютером
2. Математическая логика (6 часов)
2.1. Основные понятия логики. Суждения и умозаключения. Логические правила.
2.2. Сюжетные логические задачи, основанные на нахождении соответствия между множествами. Турнирные таблицы.. Решение задач на истинные и ложные высказывания. Таблицы истинности. Лжецы и рыцари.
2.3. Принцип Дирихле в геометрии. Элементы логики высказываний.
2.4. Математические софизмы и парадоксы.
2.5. Деловая игра «Математика в работе следователя»(учащиеся разбиваются на группы: преступники, свидетели, полицейские. Основная задача: найти виновного, прийти к истинному умозаключению на основе суждений — показаний свидетелей и преступников)
2.6. Деловая игра «Математика в работе адвоката» или «Суд идет»
8.3 (Разыгрывается сюжет заседания суда. Адвокат приводит аргументы, делает умозаключения, проводит все этапы доказательства невиновности подзащитного).
3. Математическая модель «Степенная функция» (2 часа)
3.1. Степенная функция и ее график. Свойства степенной функции
3.2. Решение практических задач из области физики, химии, биологии, географии, экономики.
4. Математические модели «Система уравнений», «система неравенств» (2 часа)
4.1. Системы уравнений и неравенств. Функционально-графический метод решения.
4.2. Решение практико-ориентированных задач из экономики, физики, химии, биологии.
5. Элементы теории вероятностей и математической статистики (3 часа)
5.1. Испытания Бернулли. Распределение Бернулли.
5.2. Числовые характеристики случайных величин. Случайные величины в статистике.
5.3. Решение практико-ориентированных задач на определение математического ожидания, дисперсии случайной величины
6. Кривые в природе и технике (6 часов)
6.1. Спирали. Спираль Архимеда. Спираль Архимеда в природе. Спираль Архимеда в машинах, преобразующих вращательное движение в поступательное. Эвольвента. Эвольвента в механизмах.
Практическая работа. «Изготовление прибора для вычерчивания эвольвенты. Построение эвольвенты».
6.2. «Золотая» спираль. Сообщения учащихся:
- Задачи, обнаруживающие золотую спираль;
- Что такое локсодрома?;
- Связь золотой спирали и «золотого сечения»;
- Золотая спираль в искусстве — застывшее мгновение;
- Золотая спираль в природе.
Практическая работа: «Построение золотой спирали с помощью «золотых» прямоугольников».
6.3. Квадратичная спираль. Спираль Корню. (траектория движения шарика по вращающемуся диску, кривая для закругления ж/д пути)
Конхоида. Никомеда. Улитка Паскаля
6.4. Трактриса. Трактриса и псевдосфера. Знакомство с геометрией Лобачевского.
Практическая работа: «Построение трактрисы на местности и на листе»
Циклоида. Часы Гюйгенса.
Практическая работа «Построение циклоиды с помощью картонного круга и линейки».
Сообщения учащихся:
Свойства циклоиды;
Удлинённая и укороченная циклоида — траектории разных точек колеса ж/д колеса;
Практическая работа: «Построение гипоциклоид с помощью шаблонов».
6.5. Синусоида. Сообщения учащихся на тему:
«Колебательные движения вокруг нас».
Практическая работа: «Построение синусоиды с помощью окружности и практическим путём с помощью трубочки из плотной бумаги и качающегося предмета».
6.6. Конические сечения и траектории движения тел, брошенных под углом. Зависимость траектории от скорости тела.
Практическая работа: «Рассечение конуса и исследование сечений».
Акустические свойства эллиптических сводов. Оптические свойства параболы. Зажигательные зеркала Архимеда — прообраз современных лазеров.
Практическая работа: «Построение гиперболы разными способами».
Оптические свойства гиперболы. Зона слышимости сверхзвукового самолёта.
Эллиптический параболоид. Гиперболический параболоид, двуполостный и однополостный гиперболоиды в архитектуре. Радиобашня на Шаболовке, Вечерний зал в Акапулько.
7. Геометрические построения и измерения на местности (4 часа)
7.1. Провешивание прямой. Нахождение точки пересечения прямых. Построение точки, симметричной относительно данной точки. Провешивание параллельной прямой.
7.2. Нахождение середины отрезка. Деление отрезка в данном отношении. Построение биссектрисы угла.
7.3. Построение перпендикуляра к прямой. Построения под заданным углом.
7.4. Измерительные работы по определению высоты дерева, расстояния до видимой, но недосягаемой точки.
8. Фракталы: наука и искусство XXI века (3 часа)
- Основные понятия. Звезда Коха. Треугольник Серпиньского. Фракталы в природе. Раковина Nautilus.
- Сложные нелинейные фракталы. Множество Жюлиа и Мандельброта
- Практическая работа: «Строим снежинку Коха» и исследуем множество Жюлиа.
9. Итоговое занятие (1 час)
Обобщение и систематизация знаний. Представление макетов, проектов, исследовательских работ.
Проведение анкетирование на предмет профессионального самоопределения.
Условия реализации программы
Методическое обеспечение
Формы организации занятий
Программа предусматривает применение различных форм работы: индивидуальной (при выполнении самостоятельной работы), в парах (при выполнении лабораторной работы), в малых группах по 5 человек (например, при осуществлении поиска алгоритма решения предложенной задачи).
Работа в парах также осуществляется при подготовке к выставке, защите проектных работ для итоговой конференции. Возможно и индивидуальное выполнение исследования.
Структура занятий
Занятия включают теоретическую и практическую части. Учащихся знакомят с новыми понятиями, которые не изучаются в рамках учебных предметов (например, рассматриваются некоторые понятия экономической теории). Происходит актуализация материала, изученного ранее в курсе физики, химии, биологии, расширение математических знаний.
Практические занятия предполагают работу учащихся в компьютерном классе. В связи с этим в начале каждого года проводится инструктаж по технике безопасности.
В конце занятия обучающиеся получают задание по подготовке к следующему занятию.
Методы работы на занятии
По характеру учебно-познавательной деятельности:
- объяснительно-иллюстративный: объяснение, работа с учебником, демонстрация моделей и т. д.;
- репродуктивный: воспроизведение действий по применению знаний на практике, деятельность по алгоритму;
- проблемное изложение изучаемого материала;
- частично-поисковый, или эвристический метод;
- исследовательский метод, когда учащимся предлагается познавательная задача, которую они решают самостоятельно, подбирая для этого необходимые методы и пользуясь помощью учителя (осуществление самостоятельного решения задачи, выполнение лабораторной работы, работа над проектом).
Материальное обеспечение
Занятия проводятся в учебном кабинете математики или информатики.
Для реализации задач программы необходимы следующие дидактические материалы и инструменты:
1. Компьютер, подключенный к сети Интернет, мультимедийный проектор, экран или интерактивная доска, принтер.
2. Для лабораторных работ — компьютерная техника для каждого учащегося с соответствующим программным обеспечением.
3. Программные средства обучения (программы — графопостроители, интерактивные модели реальных процессов)
4. Методическая, учебная литература по всем разделам учебно-тематического плана.
Литература:
1. Азевич А. И. Двадцать уроков гармонии. Гуманитарно- математический курс. — М.: Школа — Пресс, 1998. — 160с.: ил.
2. Алешина Т. Н. Урок математики: применение дидактических материалов с профессиональной направленностью. — М.: Высшая школа, 1991. — 64с.
3. Бродский И. Л., Видус А. М. и др. Сборник тестовых задач по математике для профилтных классов. 7–11 классы/ под.ред.И. Л. Бродского. — М.: АРКТИ, 2004. — 140с.
4. Симонов А. С. Экономика на уроках математики/Библиотека журнала «Математика в школе». — М.: Школа — Пресс, 1999. — 160с.
5. Сборник задач по математике с практическим содержанием. — М.: Высшая школа, 1968. — 109с.
6. Фридман Л. М. Теоретические основы методики обучения математике. Учебное пособие. — М.: Едиториал УРСС, 2005. — 248с.
7. Фоминых Ю. Ф. Прикладные задачи по алгебре для 7–9 классов. Кн.для учителя. — М.: Просвещение, 1999. — 112с.:ил.
8. Энциклопедия для детей. Т 11. Математика/ под ред. М. Д. Аксенова. — М.: Аванта +, 2002. — 688с.: ил.
9. Волошинов А. В. Математика и искусство. — 2-е изд., дораб. и доп. — М: Просвещение, 2000. — 399с.: ил.
10. Программа- графопостроитель «АвтоГраф», 2008 г.
11. «Живая Статистика 1.05", среда для проведения статистических исследований, для OC Windows







