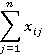Одной из ключевых проблем пассажирских перевозок в крупных городах является увеличение количества легковых автомобилей населения. Нарастающие темпы автомобилизации влекут за собой увеличение интенсивности движения на городских дорогах. Количество заторов на дорожной сети с каждым годом растет. В Волгоградской области за последние 10 лет увеличение количества автомобилей на тысячу жителей произошло на 61 % (см. рисунок 1). Как правило, основное увеличение происходит областном и районных центрах области.
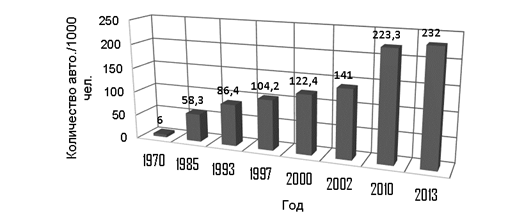
Рис. 1. Уровень автомобилизации в Волгоградской обл.
Увеличение количества автомобилей обосновано желанием населения использовать собственный автомобильный транспорт как наиболее комфортный вид передвижения, кроме этого выявлена неудовлетворенность услугами пассажирских перевозок с точки зрения регулярности движения на маршрутах общественного транспорта, что в конечном итоге приводит к снижению количества перевезенных пассажиров с каждым годом. По данным полученным от ПТП № 7 по автобусному маршруту № 6 число перевезенных пассажиров за период 2013–2014 годов снизилось на 10.9 % составило: 613147 пассажира.
Для ответа на вопрос какие именно факторы в большей или меньшей степени повлияли на величину пассажиропотока и как прогнозировать его изменение относительно изменения факторов, была построена регрессионная модель на основе исследования пассажиропотока маршрута № 6.
В ходе построения регрессионной модели были выполнены следующие задачи:
1) определение целевой функции и факторов, влияющих на целевую функцию;
2) выявление зависимости факторов между собой;
3) составление уравнения регрессии;
4) проверка адекватности полученной модели
В качестве целевой функции был выбран пассажиропоток Y.
Также были выбраны факторы, влияющие на целевую функцию, подобраны методом опроса экспертов:
Ф1 — погодные условия;
Ф2 — время суток;
Ф3 — праздничные дни;
Ф4 — сезонность;
Ф5 — стоимость проезда;
Ф6 — интервал движения ТС;
Ф7 — удобство расположения остановки;
Ф8 — техническое состояние ТС;
Следующим этапом построения регрессионной модели было Отсеивание факторов методом ранговой корреляции.
Специалистам предлагается дать оценку каждому фактору путем присвоения ему рангового номера. Фактору может присваиваться ранг от 1 до n (число факторов). При этом фактору, которому специалист дает наивысшую оценку, присваивается ранг 1. Если специалист признает несколько факторов равнозначными, то им присваивается одинаковый ранговый номер. Такие ранги носят название «связанные».
Таблица 1
Матрица рангов
|
Факторы |
Эксперты |
|||
|
1 |
2 |
3 |
4 |
|
|
Ф1 |
5 |
4 |
5 |
5 |
|
Ф2 |
1 |
1 |
1 |
1 |
|
Ф3 |
6 |
4 |
6 |
4 |
|
Ф4 |
4 |
5 |
3 |
6 |
|
Ф5 |
2 |
2 |
2 |
3 |
|
Ф6 |
3 |
3 |
4 |
2 |
|
Ф7 |
7 |
6 |
7 |
7 |
|
Ф8 |
8 |
7 |
8 |
8 |
Так как в матрице имеются связанные ранги, произведем их переформирование (табл. 2).
Таблица 2
Переформирование рангов
|
Номера мест в упорядоченном ряду |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 эксперт Расположение параметров по оценке Новые ранги |
1 X2 1 |
2 X5 2 |
3 X6 3 |
4 X4 4 |
5 X1 5 |
6 X3 6 |
7 X7 7 |
8 X8 8 |
|
2 эксперт Расположение параметров по оценке Новые ранги |
1 X2 1 |
2 X5 2 |
3 X6 3 |
4 X1 4,5 |
4 X3 4,5 |
5 X4 6 |
6 X7 7 |
7 X8 8 |
|
3 эксперт Расположение параметров по оценке Новые ранги |
1 X2 1 |
2 X5 2 |
3 X4 3 |
4 X6 4 |
5 X1 5 |
6 X3 6 |
7 X7 7 |
8 X8 8 |
|
4 эксперт Расположение параметров по оценке Новые ранги |
1 X2 1 |
2 X6 2 |
3 X5 3 |
4 X3 4 |
5 X1 5 |
6 X4 6 |
7 X7 7 |
8 X8 8 |
На основании переформированных рангов строится новая матрица рангов (табл. 3),
где 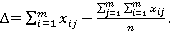
Например, 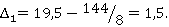
Таблица 3
Матрица рангов после переформирования
|
Факторы |
Эксперты |
Сумма рангов |
Δ |
Δ2 |
|||
|
1 |
2 |
3 |
4 |
||||
|
Ф1 |
5 |
4,5 |
5 |
5 |
19,5 |
1,5 |
2,25 |
|
Ф2 |
1 |
1 |
1 |
1 |
4 |
-16 |
196 |
|
Ф3 |
6 |
4,5 |
6 |
4 |
20,5 |
2,5 |
6,25 |
|
Ф4 |
4 |
6 |
3 |
6 |
19 |
1 |
1 |
|
Ф5 |
2 |
2 |
2 |
3 |
9 |
-9 |
81 |
|
Ф6 |
3 |
3 |
4 |
2 |
12 |
-6 |
36 |
|
Ф7 |
7 |
7 |
7 |
7 |
28 |
10 |
100 |
|
Ф8 |
8 |
8 |
8 |
8 |
32 |
14 |
196 |
|
|
36 |
36 |
36 |
36 |
144 |
- |
S=618,5 |
Проверка правильности составления матрицы на основе исчисления контрольной суммы:
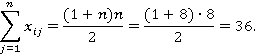
Суммы всех столбцов матрицы равны между собой и контрольной сумме. Значит, матрица составлена правильно.
. Исходя из условий ранжирования, параметр с наименьшей суммой рангов имеет наибольшее значение и, наоборот, параметр с наибольшей суммой рангов оценивается как наименее важный. Рассматриваемые параметры по значимости распределились следующим образом (табл. 4).
Таблица 4
Распределение параметров по значимости
|
Параметры |
X2 |
X5 |
X6 |
X4 |
X1 |
X3 |
X7 |
X8 |
|
Сумма рангов |
4 |
9 |
12 |
19 |
19,5 |
20,5 |
28 |
32 |
Для наглядности полученных результатов оценок параметров построим гистограмму распределения сумм рангов (рис. 2).
Построив среднюю линию, мы избавляемся от незначимых факторов. В итоге значимыми факторами являются: Ф2 — время суток, Ф5 — стоимость проезда, Ф6 — интервал движения ТС.
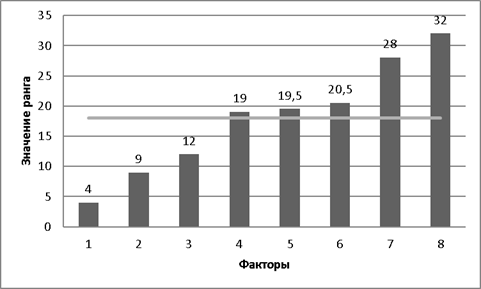
Рис. 2. Гистограмма распределения рангов
Воспользуемся коэффициентом конкордации для случая, когда имеются связанные ранги.
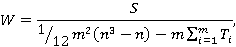
где S=618,5; n=8; m=4.
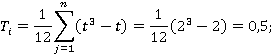
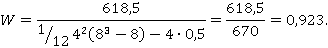
W=0,923 говорит о наличии высокой степени согласованности мнений экспертов. На высокую степень согласованности мнений экспертов указывает и полигон распределения сумм рангов.
Для этой цели исчислим критерий согласия Пирсона — χ2 по формуле:
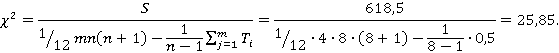
Вычисленный χ2 = 25,85 сравним с табличным значением χ2 для числа степеней свободы К=n-1=8–1=7 и при заданном уровне значимости α = 0,05. Так как 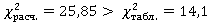 , то W=0,923 — величина неслучайная, а потому полученные результаты по оценке факторов, влияющих на пассажиропоток могут использоваться в дальнейших исследованиях.
, то W=0,923 — величина неслучайная, а потому полученные результаты по оценке факторов, влияющих на пассажиропоток могут использоваться в дальнейших исследованиях.
Для оценки тесноты связи факторов использовали коэффициент корреляции R, который характеризует тесноту связи между случайными величинами (x, y), может быть рассчитан по формуле:
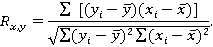
Коэффициент корреляции R характеризует тесноту связи между случайными величинами (x, y), может быть рассчитан по формуле:
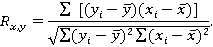
Результаты эксперимента сводили в таблицу:
Таблица 5
Значения целевой функции и факторов
|
№ |
Y |
X2 |
X5 |
X6 |
|
1 |
39 |
6:00 |
12 |
7,5 |
|
2 |
62 |
6:30 |
12 |
7,5 |
|
3 |
67 |
7:00 |
15 |
3,75 |
|
4 |
86 |
7:30 |
12 |
3,75 |
|
5 |
119 |
8:00 |
15 |
5 |
|
6 |
110 |
8:30 |
15 |
3,75 |
|
7 |
67 |
9:00 |
12 |
3,75 |
|
8 |
108 |
9:30 |
12 |
3,33 |
|
9 |
51 |
10:00 |
15 |
4,29 |
|
10 |
65 |
10:30 |
12 |
6 |
|
11 |
63 |
11:00 |
15 |
5 |
|
12 |
56 |
11:30 |
15 |
5 |
|
13 |
43 |
12:00 |
15 |
4,29 |
|
14 |
56 |
12:30 |
12 |
6 |
|
15 |
72 |
13:00 |
12 |
5 |
|
16 |
56 |
13:30 |
15 |
4,29 |
|
17 |
67 |
14:00 |
12 |
5 |
|
18 |
96 |
14:30 |
12 |
4,29 |
|
19 |
144 |
15:00 |
12 |
4,29 |
|
20 |
202 |
15:30 |
15 |
10 |
|
21 |
177 |
16:00 |
12 |
5 |
|
22 |
203 |
16:30 |
12 |
5 |
|
23 |
195 |
17:00 |
15 |
5 |
|
24 |
51 |
17:30 |
15 |
10 |
|
№ |
Y |
X2 |
X5 |
X6 |
|
25 |
105 |
18:00 |
12 |
6 |
|
26 |
29 |
18:30 |
12 |
5 |
|
27 |
38 |
19:00 |
15 |
5 |
|
28 |
106 |
19:30 |
15 |
10 |
|
29 |
7 |
20:00 |
20 |
10 |
|
30 |
42 |
20:30 |
20 |
10 |
|
31 |
25 |
21:00 |
20 |
15 |
|
32 |
19 |
21:30 |
20 |
15 |
Так как значения факторов имеют разные размерности, пронормируем их.
Таблица 6
Нормированные значения факторов
|
№ |
Y |
X2 |
X5 |
X6 |
|
1 |
39 |
-1,00 |
-1,00 |
-0,29 |
|
2 |
62 |
-0,94 |
-1,00 |
-0,29 |
|
3 |
67 |
-0,87 |
-0,25 |
-0,93 |
|
4 |
86 |
-0,81 |
-1,00 |
-0,93 |
|
5 |
119 |
-0,74 |
-0,25 |
-0,71 |
|
6 |
110 |
-0,68 |
-0,25 |
-0,93 |
|
7 |
67 |
-0,61 |
-1,00 |
-0,93 |
|
8 |
108 |
-0,55 |
-1,00 |
-1,00 |
|
9 |
51 |
-0,48 |
-0,25 |
-0,84 |
|
10 |
65 |
-0,42 |
-1,00 |
-0,54 |
|
11 |
63 |
-0,35 |
-0,25 |
-0,71 |
|
12 |
56 |
-0,29 |
-0,25 |
-0,71 |
|
13 |
43 |
-0,23 |
-0,25 |
-0,84 |
|
14 |
56 |
-0,16 |
-1,00 |
-0,54 |
|
15 |
72 |
-0,10 |
-1,00 |
-0,71 |
|
16 |
56 |
-0,03 |
-0,25 |
-0,84 |
|
17 |
67 |
0,03 |
-1,00 |
-0,71 |
|
18 |
96 |
0,10 |
-1,00 |
-0,84 |
|
19 |
144 |
0,16 |
-1,00 |
-0,84 |
|
20 |
202 |
0,23 |
-0,25 |
0,14 |
|
21 |
177 |
0,29 |
-1,00 |
-0,71 |
|
22 |
203 |
0,35 |
-1,00 |
-0,71 |
|
23 |
195 |
0,42 |
-0,25 |
-0,71 |
|
24 |
51 |
0,48 |
-0,25 |
0,14 |
|
25 |
105 |
0,55 |
-1,00 |
-0,54 |
|
26 |
29 |
0,61 |
-1,00 |
-0,71 |
|
27 |
38 |
0,68 |
-0,25 |
-0,71 |
|
28 |
106 |
0,74 |
-0,25 |
0,14 |
|
29 |
7 |
0,81 |
1,00 |
0,14 |
|
30 |
42 |
0,87 |
1,00 |
0,14 |
|
31 |
25 |
0,94 |
1,00 |
1,00 |
|
32 |
19 |
1,00 |
1,00 |
1,00 |
Далее вычислим значения коэффициентов частной корреляции.
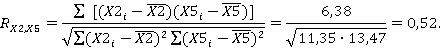
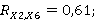
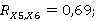
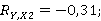
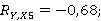
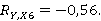
Таблица 7
Расчет коэффициентов частной корреляции
|
Y |
X2 |
X5 |
X6 |
|
|
Y |
1 |
-0,31 |
-0,68 |
-0,56 |
|
X2 |
-0,31 |
1 |
0,52 |
0,61 |
|
X5 |
-0,68 |
0,52 |
1 |
0,69 |
|
X6 |
-0,56 |
0,61 |
0,69 |
1 |
*-коэффициенты расcчитаны в программе Excel
Так как между факторами не наблюдается тесной связи, то далее составляем трехфакторную регрессионную модель.
Для определения регрессионной модели построим корреляционные поля (рис.3–5):
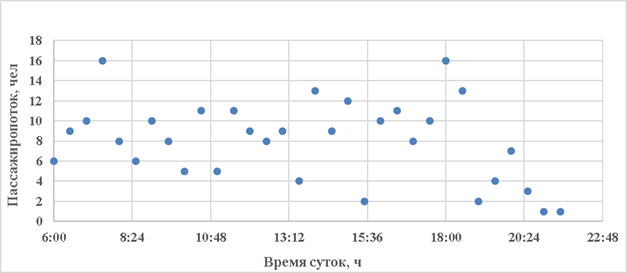
Рис. 3. Зависимость пассажиропотока от времени суток
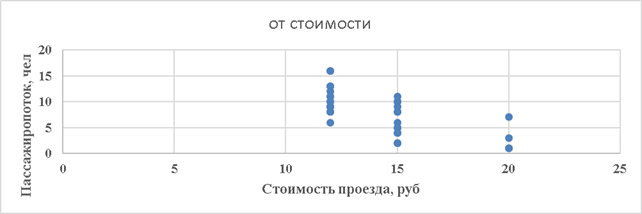
Рис. 4. Зависимость пассажиропотока от стоимости проезда
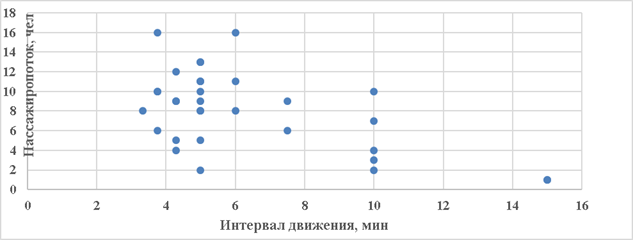
Рис. 5. Зависимость пассажиропотока от интервала движения ТС
Ввиду того, что построение регрессионной модели производится в учебных целях, то воспользуемся линейной моделью.
Общий вид линейной модели:
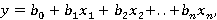
где 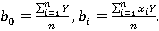
Составим матрицу планирования эксперимента (табл. 8).
Таблица 8
Матрица планирования экспериментов
|
№ |
Y |
X2 |
X5 |
X6 |
|
1 |
6 |
-1,00 |
-1,00 |
-0,29 |
|
2 |
9 |
-0,94 |
-1,00 |
-0,29 |
|
3 |
10 |
-0,87 |
-0,25 |
-0,93 |
|
4 |
16 |
-0,81 |
-1,00 |
-0,93 |
|
5 |
8 |
-0,74 |
-0,25 |
-0,71 |
|
6 |
6 |
-0,68 |
-0,25 |
-0,93 |
|
7 |
10 |
-0,61 |
-1,00 |
-0,93 |
|
8 |
8 |
-0,55 |
-1,00 |
-1,00 |
|
9 |
5 |
-0,48 |
-0,25 |
-0,84 |
|
10 |
11 |
-0,42 |
-1,00 |
-0,54 |
|
11 |
5 |
-0,35 |
-0,25 |
-0,71 |
|
12 |
11 |
-0,29 |
-0,25 |
-0,71 |
|
13 |
9 |
-0,23 |
-0,25 |
-0,84 |
|
14 |
8 |
-0,16 |
-1,00 |
-0,54 |
|
15 |
9 |
-0,10 |
-1,00 |
-0,71 |
|
16 |
4 |
-0,03 |
-0,25 |
-0,84 |
|
17 |
13 |
0,03 |
-1,00 |
-0,71 |
|
18 |
9 |
0,10 |
-1,00 |
-0,84 |
|
19 |
12 |
0,16 |
-1,00 |
-0,84 |
|
20 |
2 |
0,23 |
-0,25 |
0,14 |
|
21 |
10 |
0,29 |
-1,00 |
-0,71 |
|
22 |
11 |
0,35 |
-1,00 |
-0,71 |
|
23 |
8 |
0,42 |
-0,25 |
-0,71 |
|
24 |
10 |
0,48 |
-0,25 |
0,14 |
|
25 |
16 |
0,55 |
-1,00 |
-0,54 |
|
26 |
13 |
0,61 |
-1,00 |
-0,71 |
|
27 |
2 |
0,68 |
-0,25 |
-0,71 |
|
28 |
4 |
0,74 |
-0,25 |
0,14 |
|
29 |
7 |
0,81 |
1,00 |
0,14 |
|
30 |
3 |
0,87 |
1,00 |
0,14 |
|
31 |
1 |
0,94 |
1,00 |
1,00 |
|
32 |
1 |
1,00 |
1,00 |
1,00 |
|
Сумма |
257 |
- |
- |
- |
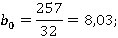
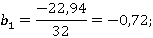
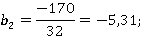
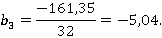
Таким образом получаем модель вида:
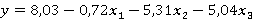 ,
,
где x1 — время суток;
x2 — стоимость проезда;
x3 — интервал движения ТС.
Затем проводим проверку значимости коэффициентов регрессионной модели по критерию Стьюдента
Статистическиу значимость каждого из факторов проверяем по соотношению критерия Стьюдента, рассчитанного по величине коэффициента регрессии и погрешности опыта, с табличным критерием Стьюдент 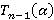 (
(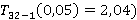 :
:
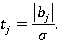
Погрешность опыта определяется величиной среднекваратического отклонения σ:
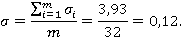
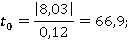
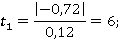
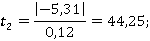
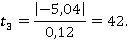
Все расчетные значения больше табличного значения критерия Стьюдента, следовательно все коэффициенты статистически значимые.
Далее необходима проверка модели на адекватность по критерию Фишера
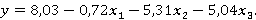
В соответствии с моделью определяем нормированные значения функции 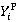 для каждого из m опытов в соответствии с планом эксперимента (табл.9). Далее рассчитываем среднеквадратичные отклонения моделей и относительно экспериментально определенных значений исследуемой функции,
для каждого из m опытов в соответствии с планом эксперимента (табл.9). Далее рассчитываем среднеквадратичные отклонения моделей и относительно экспериментально определенных значений исследуемой функции,
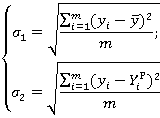
И определяем критерий Фишера
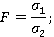
или
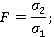
Подставляя в числитель большее из двух среднеквадратичных отклонений.
Расчет среднеквадратичных отклонений
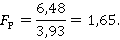
Рассчитанное значение сравниваем с табличным: FР=1,65<Fтабл(4, 28, 0,05)=2,7
Следовательно модель является адекватной.
В результате проделанной работы была получена регрессионная модель вида: 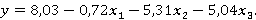 Следует заметить, что факторы x1, x2 и x3 следует подставлять в модель, в нормированном виде. Исходя из этого можно сделать вывод, что для повышения пассажиропотока необходимо уменьшать стоимость проезда (x2) и интервалы движения (x3) и, с течением времени суток (x1), в среднем, наблюдается некоторое уменьшения пассажиропотока.
Следует заметить, что факторы x1, x2 и x3 следует подставлять в модель, в нормированном виде. Исходя из этого можно сделать вывод, что для повышения пассажиропотока необходимо уменьшать стоимость проезда (x2) и интервалы движения (x3) и, с течением времени суток (x1), в среднем, наблюдается некоторое уменьшения пассажиропотока.
Т.о. при стоимость проезда 12 руб. (x2=-1,00) и интервале движения ТС 3мин 20с (x3 =-1,00) в 9.00 утра (x1=-0,61) пассажиропоток (y) будет равен:
у = 8,03–0,72 * (-0,61) — 5,31* (-1) — 5,04* (-1) = 18,8 » 19 человек.
Литература:
1. Бутакова, М. М. Экономическое прогнозирование: методы и приемы практических расчетов: учеб. пособие / М. М. Бутакова. — 2-е изд., испр. — М.: КНОРУС, 2010. — 168 с.
2. Ванин, В. А. Научные исследования в технологии машиностроения: учеб. пособие / В. А. Ванин, В. Г. Однолько, С. И. Пестрецов, В. Х. Фидаров, А. Н. Колодин. — Тамбов: Изд-во Тамб. гос. техн. ун-та, 2009. — 232 с.
3. Дрейпер Н., Смит Г. Прикладной регрессионный анализ: В 2-х кн. Кн. 1/ Пер. с англ.— 2-е изд., перераб. и доп. — М.: Финансы и статистика, 1986.— 366 с.
4. Корреляционно–регрессионный анализ [Электронный ресурс]. — Режим доступа: http://www.xliby.ru/nauchnaja_literatura_prochee/teorija_statistiki_ konspekt_lekcii/p13.php
5. Тарасевич, В. М. Ценовая политика предприятия. 2-е изд. / В. М. Тарасевич. — СПб.: Питер, 2003. — 288 с.
6. Ферстер, Э. Методы корреляционного и регрессионного анализа: руководство для экономистов / Э. Ферстер, Б. Ренц. — М.: Финансы и статистика, 1983. — 293 с.