Модель используется как рабочий инструмент познания и одновременно выполняет функции объективного подобия, более точного приближения к определенному подобию исследуемого объекта: информатора «новых, еще не открытых и неизученных свойств, допускающих опытную проверку: образно–материального восприятия труднодоступных или вовсе недоступных наблюдению свойств или структур. Предусматривается также наличие достаточно четких правил переноса информации с модели на оригинал [1].
На втором этапе создается система знаний о теле или совокупности тел, которая трансформируется в научную теорию, где модели по мере ее развития также развиваются, а иногда и полностью заменяются новыми.
Процесс познания, в конечном счете, начинается с рассмотрения и изучения конкретных тел и их свойств – непосредственного живого созерцания. Галилео Галилей наблюдал свободное падение тел. Но никто до него не пытался представить это в виде модели. Знаменитые опыты Галилея по наблюдению за падением тел с наклонной Пизанской башни – первый пример научного моделирования природного процесса [3,5].
И.Ньютону человечество обязано разработкой научных основ моделирования, которые он сформулировал во второй книге «Математические начала натуральной философии» в двух теоремах о подобии. Его наглядная модель световых явлений (механическая модель света) и описание на ее основе различных световых явлений, в частности, корпускулярных, а также создание абстрактных моделей механических взаимодействий, приведшее к обобщению и: теоретическому описанию разнообразных по внешним проявлениям физических явлений и выводу законов динамики, положили начало развитию моделирования как метода теоретического познания. Уже на основе метода моделирования был сформулирован знаменитый закон Всемирного тяготения, который потребовал от И.Ньютона шестнадцатилетних размышлений и создания совершенно абстрактной по тем понятиям модели взаимодействия небесных тел в виде системы материальных точек. Только при таком допущении оказалась справедливой формула: 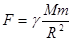 , описывающая гравитационное взаимодействие [2,4].
, описывающая гравитационное взаимодействие [2,4].
Эти примеры убеждают, что только в результате изучения конкретных тел и явлений человек приходит к общим абстракциям (понятиям, законам и другим теоретическим выводам). Наблюдения, факты, а затем модель, подкреплённая следствием и экспериментом–таков путь познания. Как видим, моделирование выступает как метод теоретического познания. Модели являются мощным средством дальнейшего, более глубокого и разностороннего познания [6].
В физике очень часто применяется метод модельного сравнения–аналогий, как один из примеров теоретического познания. Остановимся для примера на таком вопросе, как колебательные движения и волны. Описание различных по природе колебательных и волновых движений одинаковыми математическими уравнениями стало возможно благодаря созданию аналогичных, подобных моделей. Если в механизме рассматриваются колебания материальных точек, связанных между собой силами гравитации или упругости, то в электродинамике модель колебательного движения– колебательный контур, где рассматриваются колебания зарядов и полей [7,8,9].
В первом случае используется модель 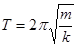 жесткой инерционной группы, во втором–инерционного контура, состоящего из катушки и ёмкости, соединенных, активным сопротивлением. Проводится физическая аналогия между величинами и на этих принципах устанавливается модельная схожесть двух явлений. (рис–1).
жесткой инерционной группы, во втором–инерционного контура, состоящего из катушки и ёмкости, соединенных, активным сопротивлением. Проводится физическая аналогия между величинами и на этих принципах устанавливается модельная схожесть двух явлений. (рис–1). 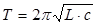
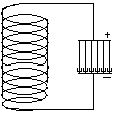
Рис. 1.
Аналогичные модели как метод теоретического познания используются во всех разделах физики. В качестве ещё одного яркого примера можно привести математическую модель полей, для описания которых вводятся подобные характеристики — напряжённость и потенциал, хотя характер, природа полей различны (например, электростатического и гравитационного).
Теоретическое моделирование особенно широко представлено в атомной и ядерной физике. Начав свою историю с квантового осциллятора М. Планка, модели в атомной и ядерной физике рассматривают сегодня структуру не только атомов, но и ядер, и их «частиц» – протона, нейтрона, других «элементарных» представлений [10,11].
Характер аналогий в физических процессах рассматривается здесь в полной мере для создания иллюзорной «наглядности» и применения ее как для всестороннего анализа, так и математической интерпретации полученных результатов. Капельная модель ядра, созданная в 30–е годы Я. И. Френкелем, имеет свою аналогию в молекулярных процессах на пограничных слоях. Все последующие ядерные модели: оптическая, оболочечная, сверхпроводящая, обобщённая модель поверхности колебаний, модель асимметричного волчка Давыдова–Филиппова также основываются на аналогиях, таких, например, как атомные и молекулярные системы и их взаимодействия [12]. Из приведённых примеров видно, что модель является одним из узловых пунктов познания. Она концентрирует в себе, по существу, все научные сведения, полученные людьми, и одновременно, служит средством дальнейшего познания объективной действительности, аппаратом научного мышления, методологическим оружием учёных, позволяющим намечать путь научного исследования. Основываясь на работах В. Г. Разумовского, можно привести такую схему научного познания: «факты–модель–следствия–эксперимент». Здесь модели отводится не только функция обобщения фактов, но она служит и методом дальнейшего познания. Благодаря модельным представлениям, возможны и опытная проверка, и предсказания ещё неизвестных науке следствий, установление научных законов. Закон, выражая общее, существенное в массе явлений, концентрацию добытых человеком знаний, может быть открыт на моделях и проверен на них.
Возникшие в последние годы материальные модели помогают понять поведение дорогостоящих систем и сооружений в реальных условиях. Модели гидроузлов, летательных сложных космических систем и уникальных энергетических установок служат не только методом познания, но и позволяют сэкономить колоссальные материальные средства для народного хозяйства.
Именно поэтому метод моделирования прочно вошёл в арсенал конструкторских бюро и проектных институтов и является необходимым условием для проектирования сложных систем и архитектурных сооружений. Большое значение имеют моделирование природных ресурсов, а также вопросы экологии [13].
Выше уже говорилось о том, что в науке модели используются для объяснения различных явления и процессов. Интерпретаторские функции моделей особенно необходимы в настоящее время, когда расширились границы познания.
Современная физика достигла двух пределов линейных размеров: в сторону мегамира порядок линейных размеров определяется в 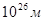 , в то время как граница микромира проходит у линейного размера порядка
, в то время как граница микромира проходит у линейного размера порядка 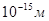 . И в первом, и во втором случаях явления, протекающие вблизи этих границ, можно только интерпретировать на моделях. Поэтому основной метод познания здесь–моделирование (в основном математическое). Что же представляет собой процесс моделирования как метод познания? Здесь можно выделить несколько этапов, каждый из которых сам служит ступенькой познания окружающего нас реального мира [14].
. И в первом, и во втором случаях явления, протекающие вблизи этих границ, можно только интерпретировать на моделях. Поэтому основной метод познания здесь–моделирование (в основном математическое). Что же представляет собой процесс моделирования как метод познания? Здесь можно выделить несколько этапов, каждый из которых сам служит ступенькой познания окружающего нас реального мира [14].
Первый этап состоит из классификации определенной совокупности свойств изучаемого предмета. Изучать одновременно все свойства тела или явления не представляется возможным вследствие их великого многообразия и разнохарактерности. Лауреат Нобелевской премии американский физик Ричард Фейнман в своем курсе лекций пишет: «Поэт сказал однажды: «Весь мир в бокале вина». Мы, вероятно, никогда не поймём, какой смысл вкладывал он в это понятие, ибо поэты пишут не для того, чтобы быть понятыми. Но, бесспорно, что, внимательно взглянув в бокал вина, мы поистине открываем целый мир. В нём и физические явления (искрящаяся) жидкость, (испарение, меняющееся в зависимости от погоды и вашего дыхания, блеск стекла (и атомы), о которых нам говорит уже наше воображение» Стекло — это очищенная горная порода: в его составе кроются секреты возраста Вселенной и развития звезд. А из какого–удивительного набора реактивов состоит это вино! Как они возникли? Там есть закваска, ферменты, вытяжки и разные другие продукты.
Ведь в вине складывается большое обобщение: вся жизнь есть брожение. Изучая химию вина, нельзя не открыть, как это сделал Луи Пастер, причины многих болезней. Сколько жизни в этом кладе, если он навязывает нашему сознанию свой дух, если мы должны быть столь осторожны с ним! Наш ограниченный ум для удобства делит этот бокал вина, этот мир на части: физику, биологию, геологию, астрономию, психологию и т. д., но ведь природа на самом деле никакого деления не знает!
Свойства тел и явлений поэтапно усложняются. Начиная изучение с самых простейших свойств – механических движений, физики переходят затем к изучению свойств и структуры твердого тела, жидкостей, газов, завершая его созданием целостной системы картины мира.
Рассмотрим в качестве примера выделение основных свойств явления для случая механического движения. Анализ многочисленных фактов приводит к выводу о том, что различные тела могут менять свое взаимное положение. Таким образом, характер явления состоит в изменении взаимного положения двух или нескольких тел с течением времени. Задача заключается в том, чтобы отыскать такие характеристики движения, которые являются общими для всего многообразия явлений данного класса. Для характеристики свойств движения вводятся: система отсчёта, координаты тел этой системы (прямоугольные Декартовы, криволинейные и т. д.) и импульс тел в выбранных координатах или другой форме (например, в векторной). Математизация явлений способствует систематизации свойств движущего тела в совокупность уравнений, которые могут иметь несколько формальных решений. Анализ решений позволяет в определённых случаях предсказать ход движения в зависимости от начальных условий и характера взаимодействия тел.
Первый этап включает в себя и создание простейшей модели. Главное требование к ней – удовлетворительное и наглядное описание явлений или свойств тела. При изучении, например, механических движений можно взять за первоначальную модель материальную точку.
Вообще говори, материальная точка, как показано во многих литературных источниках является первоосновной множество моделей различных физики, помогая понять качественные и количественные свойства различных явлений, свойств тел и структур. Следующий этап моделирования – исследование модели. Он включает в себя как классификацию ранее известных свойств, что особенно важно для получения новых знаний о теле или явлении.
Электронно-дырочная модель проводимости полупроводников, например, позволила не только объяснить электрические свойства полупроводников, но и создать на их основе множество принципиально новых приборов, сделавших революцию в радиотехнике.
Использование свойств односторонней проводимости модели определило создание, а на их базе–конструирование совершенно новых миниатюрных передающих и усилительных схем, создание быстродействующих электронно-счётных устройств и машин.
Как уже отмечалось выше, физические модели не могут претендовать и не претендуют на замену реальной природы. Поэтому одним из важных этапов создания модели является сравнение её с реальной действительностью. В методической литературе иногда встречается подмена понятий: физической модели приписывают реальное существование, или, наоборот, отождествляют ее с математической моделью.
Ни одна модель не заменяет реального тела или явления, поэтому каждая модель имеет своё применение. Опытная проверка полученных на модели знаний позволяет построить для одного и того же тела или явления несколько моделей, которые дополняют друг друга и дают более полное представление о предмете. Таким образом, метод моделирования оказывается достаточно гибким и вариативным при изучении явлений природы. Как видим, моделирование служит надёжной базой для накопления новых знаний и проверки уже известных. Поэтому оно и является одним из основных методов в познании окружающего мира.
Литература:
1. Аванесов Ю. Г. Модели и моделирование на первой ступени обучения физике. //Физика в школе. –1989. –N5. –с. 32–37.
2. Акбарходжаев З. А. Моделирование в школьном курсе физике.–Т., Укитувчи, 1990.–110 с.
3. Ахтямов А. И. Идеализация в естественно–научном познании.–Казан, Казанского университета.–1988.–190 с.
4. Борсуковский Б. А. Совершенствование процессов систематизации и обобщения знаний учащихся старших классов.–Омск, 1983.–29с.
5. Глинский Б. А. и др. Моделирование как метод научного исследования.–М., МГУ., 1965. –248 c.
6. Голин. Г. М. Вопросы методологии физики в курсе средней школы.–М., Просвещение, 1987.–127 c.
7. Икрамов ДЖ. Язык обучения математике.–Т., Укитувчи, 1989.–176 c.
8. Каменецкий С. Е., Солодухин Н. А. Модели и аналогии в курсе физики средней школы. –М., Просвещение, 1982.–96 c.
9. Салмина Н. Г. Знак и символ в обучении.–М., Изд–во, МГУ, 1988.–288с.
10. Тимченко И. И. Моделирование при изучении квантовой физики в средней школе: Дис...канд.пед.наук. –М.,1988.–203л.
11. Шодиев Д. Ш. Мысленный эксперимент в преподовании физики.–М., Просвещение, 1987.–96 c.
12. Штофф В. А. Моделирование и философия.–М.–Л.., Наука,1966.–301 c.
13. Эксперимент. Модель. Теория. — Москва–Берлин, 1982.–332 c.
14. Hager N. Modelle in der physik (erkenntnisthcoretischmetodologisck betrachtet). Berlin: Akad.–Verlag., 1982.– 182 s.







