В работе рассматривается ограниченная и самосопряженная модель Фридрихса с двумерным возмущением, который ассоциирован с системой двух квантовых частиц на трехмерной решетке. Найдены необходимые и достаточные условия для того, чтобы спектр этой модели совпадал с его числовым образом.
Ключевые слова: модель Фридрихса, числовой образ, существенный и дискретные спектры, резонанс, пороговое собственное значение.
Одним из классических методов изучения спектра линейного оператора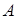 
в комплексном гильбертовом пространстве 
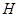с областью определения 
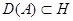является изучение его числовой области значений:
.
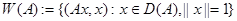Это понятие впервые введено в работе [1] и доказано, что числовой образ матрицы содержит все ее собственные значения. Вслед за этим это понятие обобщено разными способами, см. например [2–6]. Из определения множество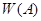 
видно, что оно является подмножеством комплексной плоскости и геометрические свойства множества 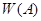дает некоторые информации об операторе 
.
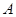Отметим, что [7] в случае, когда оператор является ограниченным и самосопряженным, замыкание числового образа есть выпуклая оболочка спектра. Возникает естественной вопрос: для каких классов ограниченных самосопряженных операторов в бесконечномерном пространстве спектр совпадает с числовым образом? Вообще, существует ли такой оператор кроме скалярного оператора? В данной статьи установлена непустота такого класса.
Пусть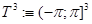 
— трехмерный куб с соответствующим отождествлением противоположных граней. Рассмотрим модель Фридрихса 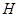, действующий в гильбертовом пространстве 
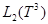квадратично-интегрируемых (комплекснозначных) функций, определенных на 
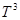по формуле
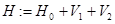
где операторы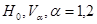 
определяются по правилам:
,
.
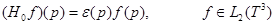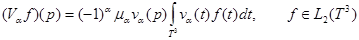Здесь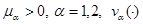 
- вещественнозначные непрерывные (ненулевые) функции на 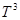, а функция 
определена как
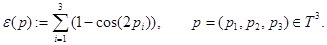
Легко можно проверить, что оператор 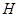, действующий в гильбертовом пространстве 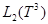, ограничен и сомасопряжен.
Рассмотрим следующие точки из :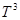
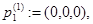
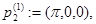
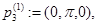
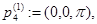
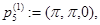
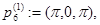
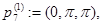
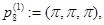
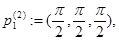
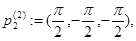
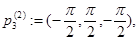
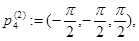
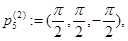
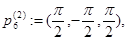
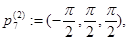
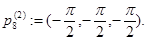
Очевидно, что функция имеет невырожденный нулевой минимум в точках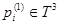 
, 
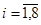и невырожденный максимум в точках 
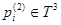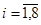, , равный 6.
Ясно, что оператор возмущения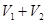 
оператора 
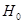является самосопряженным двумерным оператором. Поэтому из известной теоремы Г. Вейля о сохранении существенного спектра при возмущениях конечного ранга вытекает, что существенный спектр 
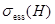оператора 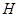совпадает с существенным спектром оператора 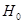. Можно показать, что 
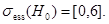Из последних двух фактов следует, что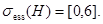 
Сформулируем следующее условие для дальнейших рассуждений.
Условие 1. Предположим, что при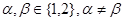 
функция 
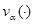является периодической по каждым переменным с периодом 
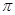, а функция 
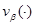удовлетворяет условию
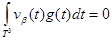(1)
для каждой функции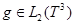 
являющийся периодической по каждым переменным с периодом .
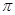Отметим, что функции вида
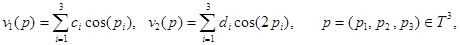
где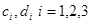 
— любые вещественные числа, удовлетворяют условию (1) с параметрами 
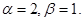Действительно, пусть 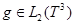есть функция как в условии 1. Тогда имеем
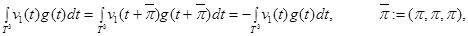
из которого вытекает справедливость равенства (1).
Наряду с оператором 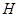, рассмотрим также ограниченный и самосопряженный оператор 
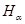, действующий в гильбертовом пространстве 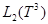по формуле 
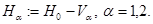При условии 1 дискретный спектр оператора 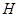совпадает с объединением дискретных спектров операторов 
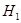и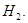 
Для удобства введем следующие постоянные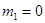 
и 
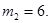Пусть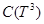 
— банахово пространство непрерывных функций, определенных на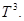 
Определение.Пусть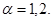 
Говорят, что оператор 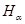имеет резонанс с энергией 
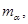если число 1является собственным значением интегрального оператора
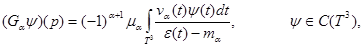
и по крайней мере одна (с точностьюдо константы) соответствующая собственная функция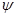 
удовлетворяет условию 
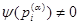при некотором 
.
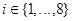Далее будем предполагать, что все частные производные второго порядка функции 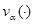непрерывны в .
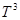Теперь перейдем к формулировке основного результата настоящей работы.
Теорема.Пусть выполняется условие 1. Верны следующие утверждения.
1) Если числа 0 и 6 являются пороговыми собственными значениями оператора 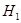и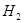 
соответственно, то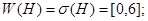 
2) Если число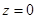 
является пороговым собственным значением оператора 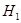, а оператор 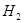имеет резонанс с энергией 
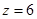, то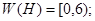 
3) Если оператор 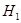имеет резонанс с энергией 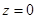и число 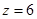является пороговым собственным значением оператора 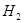, то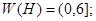 
4) Если оператор 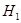и 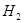имеет резонансы с энергиями 0 и 6, соответственно, то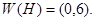 
Схема доказательство: Можно проверить, что при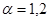 
функция
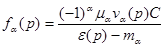
удовлетворяет уравнению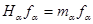 
, где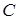 
произвольное постоянное.
Пусть
, 
;
, 
, 
.
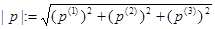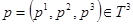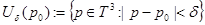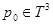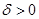Так как функция имеет невырожденный нулевой минимум в точках 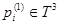, 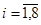и невырожденный максимум в точках 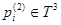, , 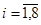равный 6, существуют числа 
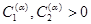и 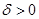такие, что
, 
, 
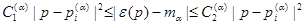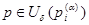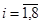. (2)
Если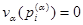 
при некотором 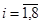, то существуют числа , 
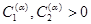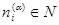и 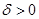такие, что
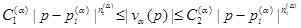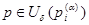, . (3)
Положим
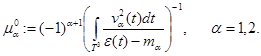
Отметим, что [8] число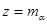 
является (пороговым) собственным значением оператора 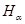тогда и только тогда, когда 
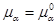и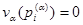 
при всех 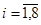. В этом случае 
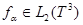и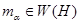 
. Кроме того, оператор 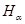имеет резонанс с энергией 
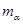тогда и только тогда, когда 
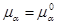и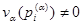 
при некотором 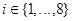. При этом 
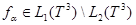и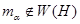 
. Эти рассуждение основаны на соотношении (2) и (3).
Следуя схеме работы [8], можно убедиться, что если оператор 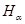имеет резонанс с энергией 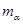или число 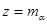является (пороговым) собственным значением оператора 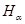, то имеет место равенство 
.
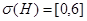Литература:
1. O. Toeplitz. Das algebraische Analogon zu einem Satze von Fejer // Math. Z., — 1918, — V. 2, — no. 1–2, — P. 187–197.
2. H. Langer, A. S. Markus, V. I. Matsaev, C. Tretter. A new concept for block operator matrices: the quadratic numerical range // Linear Algebra Appl., — 2001, — V. 330, — no. 1–3, P. 89–112.
3. L. Rodman, I. M. Spitkovsky. Ratio numerical ranges of operators // Integr. Equ. Oper. Theory, — 2011, V. 71, — P. 245–257.
4. M. T. Heydari. Numerical range and compact convex sets // Rend. Circ. Mat. Palermo, 60 (2011), 139–143.
5. H.-L. Gau, C.-K. Li, Y.-T. Poon, N.-S. Sze. Higher rank numerical ranges of normal matrices // SIAM J. Matrix Anal. Appl., 32 (2011), 23–43.
6. B. Kuzma, C.-K. Li, L. Rodman. Tracial numerical range and linear dependence of operators // Electronic J. Linear Algebra, 22 (2011), 22–52.
7. K. Gustafson, D. K. M. Rao. Numerical range: The field of values of linear operators and matrices. Springer, Berlin, 1997, 205 p.
8. Т. Х. Расулов. Асимптотика дискретного спектра одного модельного оператора, ассоциированного с системой трех частиц на решетке. Теоретическая и математическая физика. 163:1 (2010), 34–44.
