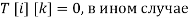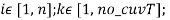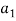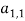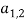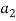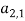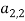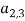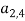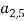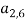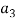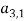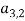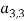Патриотическое воспитание на уроках английского языка и во внеурочной деятельности



В работе рассматриваются вопросы оптимизации процесса обучения, оптимальная организация которого является основным инструментом формирования индивидуальности обучающихся с учетом их способностей и запросов в условиях современной образовательной модели. Проблема повышения эффективности образовательного процесса рассматривается с прикладной точки зрения, проводится сравнительный обзор методов для улучшения образовательного процесса на основе генетических алгоритмов. Задачи в сфере образования, возникающие на практике, могут быть решены с использованием различных подходов и методов. Генетические алгоритмы в свою очередь используются в широком числе сфер, в основном в тех, где рассматриваются вопросы оптимизации той или иной характеристики или процесса в целом. На сегодняшний день существуют работы, посвященные внедрению новых педагогических подходов, направленных на оптимизацию учебного процесса, однако мы решили рассмотреть эту тему на примере сравнительного обзора трех вариантов использования генетического алгоритма для совершенствования конкретных образовательных подходов.

Ключевые слова: генетический алгоритм, оптимизация образовательного процесса, генерация оптимальной траектории обучения, генерация проверочных тестов.

В последние годы мы часто слышим об оптимизациях, направленных на улучшения в образовательных процессах в школах, колледжах, университетах. Задачи в сфере образования, возникающие на практике, могут быть решены с использованием различных подходов и методов, реализующих алгоритмы и использующих специальные структуры данных. Их разнообразие велико, начиная от использования деревьев и графов, заканчивая жадными или генетическими алгоритмами. Генетические алгоритмы используются для задач, в которых рассматриваются вопросы оптимизации той или иной характеристики или процесса в целом. Из названия понятно, что они были разработаны под влиянием исследований реальных генетических процессов в жизни человека, поэтому и понятия такие, как хромосомы, гены, мутация и кроссовер были позаимствованы из соответствующего раздела в биологии [1].

Генетический алгоритм — это алгоритм, который помогает найти подходящее решение к аналитически неразрешимым или сложно решаемым вопросам с помощью последовательного подбора, основанного на использовании механизмов, напоминающих биологическую эволюцию, и комбинирования искомых параметров.

Генетический алгоритм требует в реализации меньше аппаратных ресурсов, что влияет на время выполнения задачи — оно сокращается. Этот аспект важен, так как именно это является преимуществом перед другими оптимизационными или эвристическими алгоритмами, такими как поиск с возвратом (бэктрекинг), заключающийся в нахождении решений задачи, в которой требуется полный перебор всех возможных вариантов в некотором множестве [2].

На сегодняшний день существуют работы, посвященные внедрению новых педагогических подходов, направленных на оптимизацию учебного процесса [3], однако мы решили рассмотреть эту тему на примере сравнительного обзора трех вариантов использования генетического алгоритма в образовательной сфере:

1. реализация метода на основе генетических алгоритмов для генерации тестов, используемых для проверки знаний;
2. генетико-алгоритмический подход для формирования индивидуальных образовательных траекторий слушателей онлайн-курсов;
3. прогнозирование академической успеваемости студентов с помощью генетического алгоритма.

В работе кратко рассматриваются основные проблемы, решаемые представленными методами, а также выделяются ключевые характеристики методов. Полученные результаты можно использовать для анализа и применения на практике не только в образовании, возможно перенести этот опыт для решения задач и из другой области, при возможности структурировать данные схожим образом.

Метод на основе генетических алгоритмов для генерации проверочных тестов

Формирование оптимального набора тестов при наличии определенных ограничений может быть долгой и трудоемкой задачей. Сложности, с которыми обычно сталкивается преподаватель или студент: необходимо покрыть наибольшее число тем, отбор заданий должен быть выполнен на основе конкретных педагогических методов, базирующихся на опыте, изначально большое количество тестов, на основе которых должен быть сформирован итоговый набор.

В работе [3] представлен метод генерации набора проверочных тестов с помощью генетического алгоритма на основе исходного ряда тестов. Авторы связывают ряд характерных ключевых слов с тестом. Пользователь устанавливает ограничение, задавая ряд ключевых слов, которые наиболее точно отражают предмет, который он хочет протестировать. Генетический алгоритм помогает найти оптимальное решение и использует при этом меньшее количество аппаратных ресурсов.

Быстрое развитие сети Интернет создает информационный поток, который имеет свои особенности (быстрое обучение, огромные объемы данных, получаемых относительно быстро, знания, основанные на компетенции, а не на накоплении информации и т. д.). Метод же, рассматриваемый в работе [3], может быть также адаптирован к текущей динамичной интеграции IT-технологий в обучение.

Более того, время и энергия, затрачиваемые на ручную проверку тестов, очевидны. Поиск решения, сокращающего это время, является необходимостью в условиях, когда каждая минута на счету. Например, для обычного экзамена учитель создает тесты из 15 вопросов, которые образуют набор тестов. Тесты покрывают различные темы согласно образовательному плану. В процессе создания тестов преподаватель накладывает «метки» на каждый тест. При ручном поиске тестов мы предполагаем, что проверка одного теста занимает в среднем 1,5 минуты. Для набора из 150 тестов проверка занимает в общей сложности 225 минут. При правильной реализации предлагаемого метода на генерацию и идентификацию тестов в хорошо организованном наборе уйдет не более 3 минут.

Решение, представленное в работе, может быть использовано и студентами — в него заложена способность адаптации подбора тестов относительно стиля обучения. Студент может выполнить самооценку (например, при подготовке к экзаменам) по разным предметам. Более того, если набор тестов содержит вопросы из различных областей знаний, а студент хочет подготовиться только к определенным предметам за ограниченное время, проблема становится сложнее. Например, в наборе из 1000 тестов по языкам программирования, содержащем тесты по C ++, Java , PHP и JavaScript , студент должен проверить знания по Java . Для решения этой проблемы можно также использовать предлагаемый в работе метод. Что касается типов тестов, то они могут быть различными (тесты с простыми вопросами, тесты с несколькими вариантами ответов и т. д.).

Цель, которую решает предлагаемый в работе метод, заключается в генерации оптимальных тестовых наборов, содержащих максимальное количество ключевых слов из заданных пользователем.

Таким образом, основная задача алгоритма заключается в нахождении максимального количества тестов, которые могут быть выбраны после соблюдения всех заданных условий. Фитнес функцией является функция поиска максимума, и задача может быть классифицирована как задача оптимизации.

Даже если проблема не кажется срочной и необходимой, отбор тестов отнимает время и энергию. Генетический метод для генерации последовательностей был выбран за его эффективность в использовании меньших аппаратных ресурсов и за вариативность выходных решений.

Реализация метода

Тесты будут кодироваться числами от 1 до n . Оптимизированная последовательность тестов (хромосома) представляет собой расположение из k элементов, m задается пользователем (представляющее количество тестов в тестовой пуле) из набора {1, 2,..., n }, а тест (ген) в оптимизированной последовательности тестов представлен числом из множества {1, 2,..., n }. Фитнесс-функцией для оценки последовательности является максимальное количество ключевых слов в последовательности ( m — компоновкой), которые соответствуют ключевым словам, установленным пользователем. Хромосомы будут упорядочены по значению фитнес-функции. Представлен пример (рисунок 1) структуры хромосомы с 6 генами, которая будет выводиться в качестве решения.

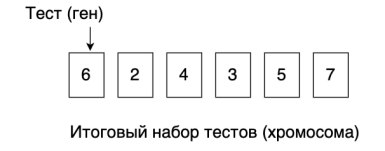
Рис. 1. Пример общего вида оптимизированной последовательности тестов (хромосом) с 6 тестами (генами)

Во-первых, массив массивов инициализируется значением 0 или 1 (ложь или истина). Целью этого массива является проверка того, является ли ключевое слово, характеризующее тест, частью ключевых слов, заданных пользователем. Затем число от 1 до n , представляющее тест, генерируется случайным образом и проверяется, входит ли одно из его ключевых слов в список ключевых слов, заданных пользователем. После этой проверки, когда оптимизированная последовательность тестов полностью сгенерирована, вычисляется значение фитнес-функции этой последовательности. Полученные последовательности тестов упорядочены по значению фитнес-функции. На следующем этапе производятся такие операции, как мутация или кроссовер между хромосомами (последовательностями). Затем полученные последовательности снова упорядочиваются по значению фитнес-функции.

Переменные, используемые в алгоритме представлены в таблице 1.

Таблица 1

Переменные, используемые в алгоритме

Наименование переменной	Описание переменной
n	количество тестов в наборе
m	количество тестов, которые необходимо получить в результирующем оптимальном наборе
no_generations	количество поколений, используемых для создания оптимального набора тестов
no_words	количество ключевых слов, заданных пользователем
no_cuvT	количество ключевых слов каждого теста

Структуры (массивы), которые потребуются в алгоритме представлены в таблице 2.

Таблица 2

Структуры данных (массивы), используемые в алгоритме

Наименование структуры данных (массива)	Описание
TG [no_words]	массив, содержащий ключевые слова, заданные пользователем
pop [no_generations] [m]	массив решений
T [n] [no_words]	массив массивов, который содержит значение 1 или 0: T [i] [k]=1, если k - ключевое слово из i - теста нашлось в TG -массиве

После представления входных данных можно сказать, что фитнес-функция имеет следующий вид:

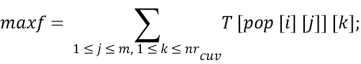
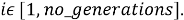
Входные данные будут сформированы из n , m , no_generations , no_words , no_cuvT и ключевых слов для каждого теста. Чтобы каждый раз не сравнивать ключевые слова, формируется массив T , в нем хранятся только те ключевые слова, которые совпадают с ключевыми словами из массива TG и тестов, содержащих их. Выходные данные будут содержать первые k решений (полученных последовательностей тестов) из массива pop , где k — значение, заданное пользователем, и количество ключевых слов, совпадающих с ключевыми словами из TG для каждой последовательности.

Опишем шаги алгоритма:

Шаг 1. Считываются входные данные (упомянутые ранее).

Шаг 2. Массив T инициализируется значениями 0 или 1 (ложь или истина) в соответствии с определением, представленным ранее.

Шаг 3. Хромосомы (оптимизированные последовательности тестов) генерируются случайным образом, ген за геном. Это будет начальная популяция.

Шаг 4. Для каждой хромосомы рассчитывается фитнес-функция. Фитнес-функция хранится в ( m + 1)-м элементе массива решений ( pop ).

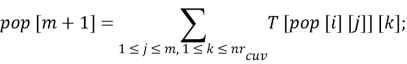
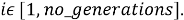
Шаг 5. Над сгенерированными хромосомами применяются операции (мутация и кроссовер). На этом шаге также рассчитывается фитнес-функция для каждой хромосомы. Фитнес-функция также хранится в ( m + 1) — м элементе массива решений. На рисунке 2 представлен пример мутации внутри хромосомы.

Рис. 2. Мутация внутри набора тестов (хромосомы)

На рисунке 3 представлен пример операции кроссовера между двумя хромосомами.

Рис. 3. Кроссовер между двумя оптимизированными последовательностями тестов (хромосом)

Шаг 6. Хромосомы упорядочиваются по значению фитнес-функции. На этом этапе можно использовать метод упорядочивания. Шаги 5 и 6 повторяются в течение no_generations раз.

Шаг 7. Выводятся первые искомые решения.

Рассмотренный алгоритм применим на практике и полезен при подготовке к проведению контрольных и проверочных работ но его применение может быть расширено в задачах, которые можно структурировать аналогичным образом (например, в области логистики, в математике и т. д.), из-за использования понятий комбинаторики. Кроме того, метод может быть расширен для формирования вопросов в рамках одного теста (оптимальные наборы последовательностей из вопросов).

Данный метод полезен для выбора конкретных тестов, имеющих некоторые ограничения, заданные пользователем, а также предназначен для получения решений за разумное время в пределах заданного диапазона.

Генетико-алгоритмический подход для формирования индивидуальных образовательных траекторий слушателей онлайн-курсов

Одним из основных направлений будущего совершенствования онлайн-курсов является возможность комплексной персонализации. Необходимость персонализации обучения является отражением естественного для человечества стремления к индивидуальному подходу к личным потребностям, предпочтениям и возможностям. Серьезным недостатком онлайн-курсов является отсутствие индивидуального и дифференцированного подхода к каждому студенту из-за заранее заданного маршрута обучения в типовых курсах. В работе [4] предложен генетический алгоритм, позволяющий сформировать оптимальный маршрут обучения, разработанный с учетом личных образовательных потребностей и индивидуальных возможностей каждого слушателя массовых открытых онлайн-курсов. Рассмотрены результаты вычислительного эксперимента и примеры индивидуальных траекторий, сформированных на основе предложенного алгоритма.

Целенаправленно разработанная индивидуальная программа обучения — это технологический инструмент для реализации индивидуального учебного маршрута. Индивидуальные учебные маршруты слушателей МООК (массовых открытых онлайн курсов) отличаются не только объемом, но и вариативностью форм представления электронного учебного контента. Это связано с индивидуальными стилями обучения слушателей и, соответственно, их видами деятельности, используемыми при изучении одного и того же учебного объекта. Невозможно заранее спроектировать индивидуальный учебный маршрут так, как он должен отражать динамику обучения, раскрывая ее в движении и изменении. Такой подход позволит своевременно вносить необходимые коррективы в образовательный процесс, реализуемый на базе МООК. Например, восполнить определенные пробелы в знаниях и навыках слушателей курса, или наоборот, ускорить процесс обучения или углубить программу обучения.

В рамках исследования МООК имеет модульную структуру, состоящую из определенного количества блоков. В рамках каждого блока существуют учебные объекты (УО) различных типов в таблице 3, которые являются структурными компонентами электронного учебного контента курса. Определенный набор учебных объектов (УО) обеспечивает формирование одной или нескольких соответствующих компетенций.

Известно, что каждый слушатель курса имеет свой собственный стиль обучения. Исследователи выделяют следующие 4 типа студентов, различающихся по доминирующему стилю обучения: учащиеся-визуалы (« V« ), учащиеся-аудиалы (« A« ), учащиеся-дигиталы (« D« ), учащиеся-кинестетики (« K« ).

К какому типу относится каждый из слушателей МООК, в работе [4] определяется в начале процесса обучения, с использованием методологии VARK. Итак, в работе каждый слушатель курса (как изучаемый объект) характеризуется следующими входными параметрами (набор атрибутов, характеризующих состояние данного объекта), которые представлены в таблице 2.

Выделяются четыре обобщенные группы типов контента в зависимости от доминирующего стиля обучения, данные представлены в таблице 3. Например, первая группа состоит из типов контента, наиболее подходящих для студентов с доминирующей модальностью «визуал». Установлено, что у студентов могут быть и смешанные модальности. На этом основании предлагается формировать курс с разными типами содержания, но при этом максимально учитывая выявленную доминирующую модальность.

Таким образом, в каждом блоке должно присутствовать определенное количество УО из списка каждой группы. Соответственно, для каждого слушателя должен быть динамически сформирован блок, состоящий из УО, в основном соответствующих его стилю обучения.

Чтобы установить репрезентативное соотношение различных типов контента (учебных объектов) конкретной единицы в зависимости от стиля обучения, в работе было опрошено 15 457 респондентов. Использование методологии VARK позволило проанализировать реальную ситуацию [5].

Таблица 3

Состав четырех обобщенных групп различного образовательного контента

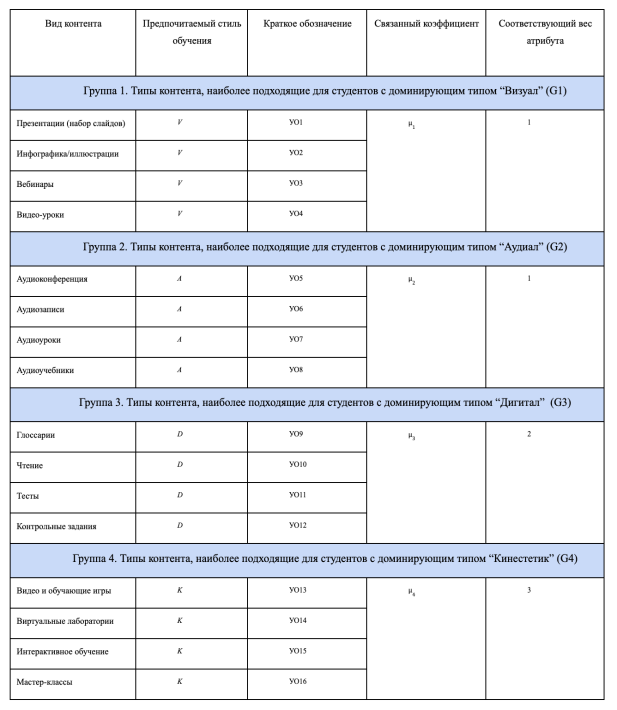
На основании результатов опроса было определено соотношение различных типов контента в конкретном онлайн-курсе для каждого студента курса.

Завершение изучения каждого раздела сопровождается выполнением итогового теста, результаты которого позволяют сделать вывод об успешности процесса обучения или преобладании трудностей в курсовом предмете.

По результатам опроса определили соотношение разных видов контента в конкретном онлайн курсе для каждого типа учащихся, данные отражены в таблице 4. Тогда сумма соотношения типов контента различных групп для каждого типа учащихся должен быть равен единице µ1 + µ2 + µ3 + µ4 = 1. Варьируя соотношение µ1, µ2, µ3, µ4 при формировании итоговой траектории можно получить различные наборы УО в индивидуальном маршруте обучения.

Таблица 4

Характеристики и значения атрибутов для набора студентов

Название характеристики	Характеристика (параметр)	Возможные значения атрибута	Значение коэффициента для атрибута	Соответствующий вес атрибута
	Пол	Женский		1
		Мужской
	Возраст группы	до 18		2
		19–25
		26–34
		35–44
		45–54
		55+
	Подход к обучению	Визуалы		3
		Аудиалы
		Дискреты
		Кинестетики

Таким образом, индивидуальный маршрут обучения в МООК представляет собой разнообразный набор учебных объектов разных типов для каждого блока. Согласно результатам экспериментов в работе [4] список может быть сформирован динамически на основе генетического алгоритма и корректироваться в режиме реального времени при переходе слушателя от одного раздела к другому.

Прогнозирование академической успеваемости студентов с помощью генетического алгоритма

Проблема прогнозирования академической успеваемости студентов становится все более актуальной благодаря накоплению больших объемов данных в базах данных университетов [2]. Прогнозирование и анализ успеваемости студентов может сыграть важную роль в академическом развитии студентов. Определение факторов, влияющих на успеваемость обучающихся является сложной исследовательской задачей [6].

Прогнозирование академической успеваемости студентов с высокой точностью будет полезным для образовательных учреждений, чтобы иметь возможность качественно влиять на ситуацию подготовки специалистов с помощью оперативной корректировки образовательного процесса [6]. Анализ данных в сфере образования может быть использован университетами при разработке образовательных стратегий, направленных на повышение качества образования.

Проблемы, которые часто встречаются в наборе данных: высокая размерность данных и шум, они могут значительно влиять на результаты прогнозирования [7]. Генетический алгоритм отбора признаков ( GAFS ) обычно используется для решения проблемы, связанной с высокой размерностью набора данных и зашумлением атрибутов [8].

В работе [6] были использованы четыре классификатора, а именно: дерево решений ( DT ), наивный байесовский классификатор ( NB ), метод ближайших соседей ( k - NN ) и метод случайного леса ( RF ) вместе с генетическим алгоритмом ( GAFS ). Для того чтобы измерить точность, используются четыре оценочных показателя, а именно: доля ошибок ( accuracy ), точность ( precision ), полнота( recall ) и F -мера. Схема разработанного в работе [4] фреймворка представлена на рисунке 4. она разделена на два этапа — выбор признаков и моделирование.

Рис. 4. Схема прогнозирования академической успеваемости учащихся [5]

На первом этапе, который представляет собой выбор признаков, набор данных разделяется на обучающие и тестовые данные. Затем используется GAFS для получения подмножества признаков для улучшения точности прогнозирования.

На втором этапе, который называется моделированием, данные обучения с выбранным подмножеством признаков обучаются. Обучение производится с помощью выбранного классификатора. Точность классификации измеряется с помощью тестового набора с выбранным подмножеством признаков. Затем вычисляется фитнес-функция, использующая классификационную точность классификатора, количество выбранных признаков и вес признака [9].

Для генетического алгоритма отбора признаков (GAFS) и классификаторов были выбраны следующие начальные параметры: размер начальной популяции (30), максимальное число поколений (30), мутации (0,01), вероятность кроссовера (0,9). При достижении конечного условия, операция будет остановлена, однако, если условия не выполнены, выполняется переход к следующему поколению операций. Система ищет лучшие решения с помощью генетических операций отбора и мутации, включая кроссовер [6].

Результат оценки с использованием классификатора со всеми признаками показан в таблице 5, а результат использования классификатора с GAFS показан в таблице 6. Использование GAFS показывает более высокое увеличение точности, чем классификаторы без использования выбора признаков.

Таблица 5

Результат работы методов классификации со всеми атрибутами

	Дерево решений	Метод ближайших соседей	Наивный байесовский классификатор	Метод случайного леса
Доля ошибок	62.71	61.04	57.50	79.79
Полнота	62.70	62.04	59.96	80.34
Точность	64.73	61.61	58.14	80.42
F-мера	63.70	61.79	58.76	80.28

Таблица 6

Результат работы методов классификации с выбором признаков на основе генетического алгоритма

	Дерево решений	Метод ближайших соседей	Наивный байесовский классификатор	Метод случайного леса
Доля ошибок	74.58	68.54	75.42	82.29
Полнота	75.15	68.84	76.25	82.81
Точность	75.39	69.75	76.26	82.70
F-мера	75.26	69.29	76.25	82.75

Следовательно, использование GAFS в методах классификации — это решение, позволяющее повысить точность прогнозирования успеваемости учащихся.

Заключение

В данной работе был проведен сравнительный обзор трех вариантов использования генетических алгоритмов на практике в задачах, направленных на оптимизацию учебного процесса. Были рассмотрены варианты практического использования генетических алгоритмов для генерации проверочных тестов, для формирования индивидуальных образовательных траекторий слушателей онлайн-курсов и при прогнозировании академической успеваемости студентов. Прикладные сферы отличаются, но ключевым выводом является возможность использовать методы на основе генетических алгоритмов для анализа и применения на практике не только в образовании, алгоритм можно адаптировать для решения задач и из других областей, например IT. Основное ограничение связано с необходимостью структурировать подходящим образом входные данные.

Литература:

1. Скиена, С. С. Алгоритмы. Руководство по разработке. 3-е изд. / С. С. Скиена. — Санкт-Петербург: БХВ, 2022. — 848 c.
2. Уилер, Т. Алгоритмы оптимизации / Т. Уилер, М. Кохендерфер. — Москва: Вильямс, 2020. — 528 c.

2. Doru, P. A. A Method Based on Genetic Algorithms for Generating Assessment Tests Used for Learning / P. A. Doru. — Текст: электронный // https://www.scielo.org.mx/: [сайт]. — URL: https://www.scielo.org.mx/scielo.php?script=sci_arttext&pid=S1870–90442016000200053 (дата обращения: 01.12.2022).
3. Zaporozhko, V. V. A genetic-algorithm approach for forming individual educational trajectories for listeners of online courses / V. V. Zaporozhko. — Текст: электронный // https://ceur-ws.org/: [сайт]. — URL: https://ceur-ws.org/Vol-2254/10000229.pdf (дата обращения: 15.02.2022).
4. Гладков, Л. А. Генетические алгоритмы / Л. А. Гладков, В. В. Курейчик, В. М. Курейчик. — Москва: Издательская фирма Физико-математическая литература, 2020. — 200 c.
5. Farissi, A. Genetic Algorithm Based Feature Selection for Predicting Student’s Academic Performance / A. Farissi. — Текст: электронный // https://www.researchgate.net/: [сайт]. — URL: https://www.researchgate.net/publication/337534319_Genetic_Algorithm_Based_Feature_Selection_for_Predicting_Student's_Academic_Performance (дата обращения: 16.01.2023).
6. Элис, Ч. Машинное обучение: Конструирование признаков. Принципы и техники для аналитиков / Ч. Элис. — Москва: Бомбора, 2021. — 240 c.
7. Николенко, С. И. Глубокое обучение / С. И. Николенко, А. А. Кадурин, Е. О. Архангельская. — Санкт-Петербург: Питер, 2022. — 480 c.
8. Будума, Н. Основы глубокого обучения. Создание алгоритмов для искусственного интеллекта следующего поколения / Н. Будума. — Москва: Манн, Иванов и Фербер, 2019. — 304 c.