В последнее время обучение архитекторов в нашей стране всё больше связано с дизайном окружающей среды, максимальное количество внимания уделяется творческой составляющей проектов, а проверка надёжности проектов уже почти не осуществляется. Десять лет назад архитекторы изучали расчётные дисциплины: «теоретическую механику», «сопротивление материалов» и «строительную механику» на уровне инженеров «Промышленно гражданского строительства», выполняя аналогичные расчётно-графические расчёты. Сейчас количество аудиторных часов на изучение этих сложных дисциплин снизилось до критического минимума. Однако проектирование современных конструкций должно «сочетать требование надёжности с экономичностью, необходимо с большей точностью произвести расчёт и строго соблюдать в процессе проектирования требования к возведению и эксплуатации сооружения, вытекающие из этого расчёта» [1 c.4].
В процессе трудовой деятельности часть бывших выпускников — архитекторов сталкивается с необходимостью расширения своих познаний в области расчётных дисциплин, и они вынуждены получать дополнительное образование на направлении «Промышленно гражданское строительство» (заочного отделения). Однако получение дополнительного образования является обязательно платным и естественно требует дополнительных материальных и временных затрат.
Дипломные студенческие работы должны нести элемент новизны и это приводит к тому, что их работы всё больше уходят в область объектов, малопригодных в реальной жизни, предлагаемые студентами конструкции зачастую практически невозможно воплотить, считается, что их расчётом должен заниматься проектировщик — инженер, владеющий соответствующей компетенцией.
Такая ситуация приводит к тому, что рассчитываются не совсем те проекты, которые хотел воплотить архитектор, от этого страдает эстетическая сторона проекта.
Таким образом, современные тенденции требуют, чтобы сам архитектор мог проектировать в первом приближении конструкции смелые, но вместе с тем надёжные; прочные, но лёгкие; красивые и экономичные. В работе над ними использование моделей не достаточно (3Д моделей или макетов, склеенных вручную из подручного материала), т. к. геометрически подобные модели не являются подобными друг другу, как в статическом, так и в динамическом смысле.
Поэтому перенос данных с модели на реальный объект без предварительных расчётов невозможен, т. к. это не обеспечит надёжность сооружений в эксплуатационных условиях. Для решения этой задачи необходимо воспользоваться методами строительной механики, которая даёт математическую теорию расчёта различных зданий и сооружений с точки зрения прочности, жёсткости и устойчивости. Эти методы прошли апробацию на широкой базе экспериментальных работ, а главное, включают в себя изучение реальных конструкций в процессе их эксплуатации. Язык этих расчётов (построенные эпюры) международный и понятен архитекторам и строителям всех стран.
Но так как архитекторы люди творческие, то сам курс «Строительной механики» желательно преподнести более живым и доступным языком. Эту задачу в ТюмГАСУ решаем с помощью комплекта рабочих тетрадей по дисциплине: «Краткий курс лекций по строительной механике», «Расчёт статически определимых конструкций» и «Расчёт статически неопределимых конструкций». Данное разбиение курса автор сочла наиболее целесообразным.
Теперь продемонстрируем, каким образом работают данные учебно-методические разработки на примере части лекции.
Лекция на тему «Расчёт статически определимых конструкций»
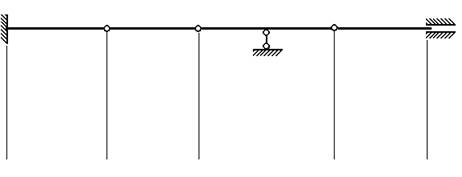
Преподаватель даёт определение статически определимых конструкций, формулирует их основные свойства, эти сведения появляются на экране преподавателя и уже записаны у студентов в рабочей тетради. Затем переходим к изучению наиболее простой конструкции — многопролётной балки. Формулируем, что такое многопролётная балка и демонстрируем её на экране, аналогичный рисунок есть у студентов в рабочей тетради, продублированный несколько раз, чтобы его в дальнейшем можно было изменять.
|
Фрагмент лекции: |
|
|
|
|
|
|
Заданная балка заведомо имеет «лишние связи».
|
|
Преподаватель предлагает определить сколько «лишних связей» у данной конструкции, как правило, все догадываются что пять, т. к. для неподвижности достаточно трёх опор. Затем проверяем своё предположение по формуле Чебышева, выведенной на первой лекции, со ссылкой на соответствующий раздел рабочей тетради.
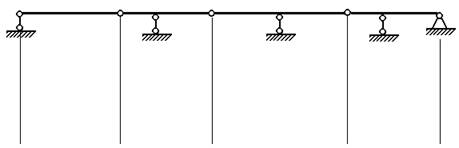
Чтобы ликвидировать «лишние связи», необходимо врезать в конструкцию пять шарниров, аудитория вместе с преподавателем решает, каким образом это будет сделано, и на ранее нарисованных балках изображает шарниры.
|
По одному на каждый пролёт, начиная со второго: а) |
|
По два произвольно: б) |
|
По два через один пустой пролёт: в) |
|
По два, включая последний: г) |
|
По три: д) |
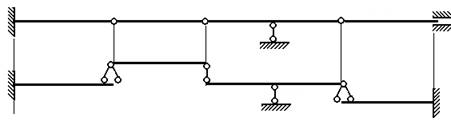
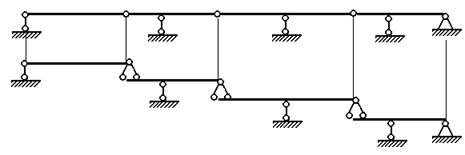
При этом студенты просто изображают шарниры на рисунках своей рабочей тетради. Далее преподаватель предлагает проанализировать данные конструкции на неизменяемость, после соответствующего анализа получаем, что балки с рисунков б), г) и д) изменяемые:
|
б) |
|
г) |
|
д) |
Студенты отображают, полученные результаты и записывают соответствующие выводы.
|
Фрагмент лекции: Правило врезки шарниров: По одному шарниру на пролёт можно врезать _____________________________________________________________________ Пролёт с двумя шарнирами должен быть отгорожен от _____________________________________________________________________ Пролёты с двумя шарнирами должны чередоваться ____________________________________________________________________ Не допускаются пролёты с___________________________________________ |
После проведённых рассуждений преподаватель предлагает способ расчёта полученных балок с помощью, так называемой поэтажной схемы. Студенты вписывают информацию в соответствующий блок рабочей тетради.
|
Фрагмент лекции: Построение эпюр в многопролётных балках начинаем с построения поэтажной схемы, т. е. балку разбиваем на:
Основную (опорную) часть, которая ______________________________________________ _____________________________________________________________________________ И подвесную, которая__________________________________________________________ _____________________________________________________________________________ Нагрузка, расположенная на опорной части, не приводит к деформации подвесных частей, а нагрузка, расположенная на подвесной части, вызывает деформацию основной части. Поэтому расчёт начинаем с «этажей». |
Затем идут примеры построения поэтажных схем
|
Фрагмент лекции:
|
|
|
Здесь обучаемые изображают рисунки и анализируют соответствующие комментарии к ним.
|
|
|
|
Приводится достаточно большое количество примеров, чтобы студенты поняли принцип построения поэтажных схем. Затем решаем простейшую двух пролётную балку.
Раньше на этом лекция заканчивалась, т. к. истекали 90 минут. Но после разработки и внедрения рабочих тетрадей появилось время для того, чтобы кратко описать ещё рамные конструкции, классифицировать составляющие их элементы и рассмотреть построение поэтажных схем в них.
Из приведённой части лекции видно, что использование рабочей тетради позволяет преподавателю не тратить время лекции или практического занятия на отрисовку схем строительной механики, иногда достаточно сложных, получать достаточно быстро ответную реакцию аудитории на задаваемые вопросы, так как студенты не заняты компиляцией слайдов и у них есть возможность добавлять какие-то свои примечания по ходу занятия. При этом наиболее важная часть материала, которую необходимо запомнить, записывается вручную. Учитывая, что студенты архитекторы в силу специфики своей профессии скрупулезно относятся к качеству изображений, раньше приходилось ожидать, пока они более красиво перерисуют чертёж в ущерб выдаваемому объёму, а долгое механическое перерисование материала с доски приводило к плохому усвоению познавательной части лекции.
Если по каким-то причинам студент пропустил занятия, то у него есть возможность самостоятельно проработать материал с помощью практически любого из рекомендованных учебников, не затрачивая на это слишком много времени, т. к. направление движения чётко обозначено.
Таким образом, использование рабочей тетради в условиях недостаточного количества аудиторных часов помогает будущим архитекторам применять методы математического анализа и моделирования, теоретического и экспериментального исследования; выявлять естественнонаучную сущность проблем, возникающих в ходе профессиональной деятельности, привлекать для их решения соответствующий физико-математический аппарат.
Литература:
1. Саргсян А. Е., Демченко А. Т., Дворянчиков Н. В., Джинчвелашвили Г. А. Строительная механика // Основы теории с примерами расчётов: Учебник/ Под ред. А. Е. Саргсяна.- 2-е изд., испр. и допол. –М. Высшая школа, 2000.