В статье рассматриваются вопросы распознавания для вариантных и инвариантных образов. А также такие вопросы как, выделение признаков с помощью моментов, приложение инвариантных моментов, логарифмически-полярные преобразования и дискретное преобразование Фурье. И предложен алгоритм для извлечения инвариантных признаков. Статья предназначена для специалистов занимающиеся вопросами распознавания образов.
Ключевые слова: распознавание образов, инвариантный образ, вариантный образ, преобразование, алгоритм, шаг.
Выделение признаков с помощью моментов
Распознавание геометрических образов независимо от позиции, ориентации и размера может быть достигнуто, используя инварианты моментов. Эти моменты единственным образом определяют кусочно-непрерывную функцию f (x, y), которая имеет ненулевые значения только в конечной части плоскости XY. Если f (x, y) — числовое отображение в двумерном пространстве, то моменты порядка (p+q) могут быть
 для p, q = 0, 1, 2, … (1)
для p, q = 0, 1, 2, … (1)
Центральные моменты могут быть выражены как
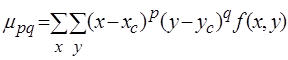 (2)
(2)
где xc = M10 / M00, yc = M01/ M00
Нормализованные центральные моменты Npq могут быть определены как
Npq = mpq / (m00)g (3)
Где, g = (p+q)/2 +1, для p+q = 2, 3, … (4)
Набор семи моментов может быть получен как инвариант преобразования трансляции, вращению и масштабирования. Эти семь моментов следующие:
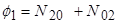 (5)
(5)
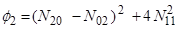 (6)
(6)
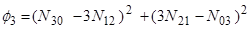 (7)
(7)
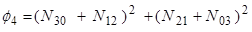 (8)
(8)
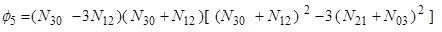
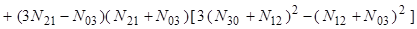 (9)
(9)
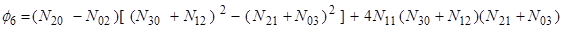 (10)
(10)
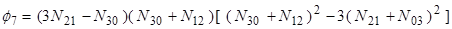
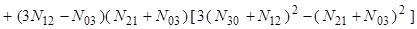 (11)
(11)
fi = log (fi) для i=1,2, …, 7 (12)
Приложение инвариантные моменты
Инвариантные моменты для цифр были рассчитаны, с использованием формул, данных. Моменты имеют малые значения, поэтому были взяты их логарифмические значения семь моментов для каждой цифры описаны в Таблице 1. Эти моменты использовались как входные данные к нейронной сети Кохенена [1]. Моменты первоначальных и преобразованных образов для цифр 2 и 3 даются, например, в таблицах (2, 3). Они показывают, что моменты являются инвариантными при преобразованиях. На рисунке 1 показано распознавание цифр от 2 до 9 при различных преобразованиях.
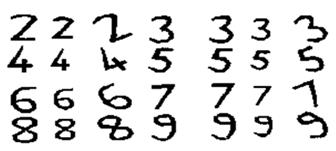
Рис. 1: Первоначальные и преобразованные цифры от 2 до 9
Таблица 1
Моменты первоначальных цифр
|
Цифры |
f1 |
f2 |
f3 |
f4 |
f5 |
f6 |
f7 |
|
0 |
0.289674 |
1.891244 |
3.081613 |
3.707944 |
7.532423 |
5.018612 |
7.135025 |
|
1 |
0.144440 |
0.316391 |
2.456137 |
2.649631 |
5.204564 |
2.824600 |
6.216168 |
|
2 |
0.178210 |
0.795665 |
2.528437 |
2.651690 |
5.293618 |
4.912113 |
5.578113 |
|
3 |
0.135953 |
0.652886 |
1.322085 |
1.968569 |
3.722268 |
2.298309 |
3.816754 |
|
4 |
0.386179 |
1.634139 |
1.370766 |
2.014032 |
3.710191 |
2.975653 |
4.589142 |
|
5 |
0.267451 |
1.044964 |
3.369814 |
2.925594 |
6.124222 |
3.448483 |
6.413185 |
|
6 |
0.260682 |
1.393926 |
1.673842 |
2.024529 |
4.094603 |
5.121104 |
3.971167 |
|
7 |
0.156055 |
0.691871 |
0.664061 |
1.250537 |
2.356787 |
1.666528 |
2.359927 |
|
8 |
0.321487 |
1.489974 |
4.330697 |
4.314062 |
9.323424 |
5.154918 |
8.64582 |
|
9 |
0.2938891 |
1.2640356 |
1.7301497 |
1.9389643 |
3.941932 |
2.956681 |
3.90750 |
Таблица 2
Моменты образов и вариантов цифры 2
|
Образ 2 |
f1 |
f2 |
f3 |
f4 |
f5 |
f6 |
f7 |
|
Первоначальный |
0.17821 |
0.795665 |
2.528437 |
2.651690 |
5.293618 |
4.912113 |
5.57811 |
|
Смещение 0,2 |
0.17975 |
0.798129 |
2.539199 |
2.633436 |
5.258346 |
4.189751 |
5.61392 |
|
Масштабирование 0,8 |
0.20006 |
0.859173 |
2.337220 |
2.912201 |
7.030966 |
3.445200 |
5.53713 |
|
Угол вращения p/6 |
0.17396 |
0.746629 |
2.275593 |
2.522349 |
4.991883 |
4.351878 |
5.19973 |
Таблица 3
Моменты образов и вариантов цифры 3
|
Образ цифры 3 |
f1 |
f2 |
f3 |
f4 |
f5 |
f6 |
f7 |
|
Первоначальный |
0.135953 |
0.652886 |
1.322085 |
1.9685698 |
3.7222681 |
2.2983096 |
3.816754 |
|
Смещение 0.2 |
0.135953 |
0.652886 |
1.322085 |
1.9685698 |
3.7222681 |
2.2983096 |
3.816754 |
|
Масштабирование 0.8 |
0.159801 |
0.690702 |
1.494270 |
2.1207083 |
3.9784019 |
2.4663624 |
4.270824 |
|
Угол вращения p/6 |
0.103264 |
0.529989 |
1.312760 |
1.9181933 |
3.6848698 |
2.4416071 |
3.683503 |
Преобразования Фурье-Меллина, были введены для регистрации образов, которые имеют нарушения границ вследствие трансляции, вращения и масштабирования. При трансляции образов этот метод использует преобразования Фурье. Затем логарифмически-полярное преобразование применяется для определения спектра величины, вращения и масштабирования с учетом фазы корреляции в логарифмически-полярном пространстве. Это преобразование является причиной вращения и масштабирования, которые есть суть трансляции [2].
Логарифмически-полярное преобразование
Сделаем обзор логарифмически-полярных координатных преобразований. Рассмотрим полярную систему координат (r,q), где r обозначает радиальное расстояние от центра (xc, yc) и q обозначает полярный угол. Любая точка изображения с координатами (x, y) может быть представлена в полярных координатах (r,q))
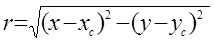 (13)
(13)
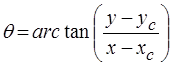 (14)
(14)
Применяя полярное координатное преобразование к изображению I, отобразим радиальные строки в декартовой системе координат к горизонтальным строкам в полярном координатном пространстве. Преобразованное изображение обозначим Ip. Преимущество этого нового координатного пространства в том, что простое масштабирование и вращение в этой системе координат могут быть получен изменением значений (r,q). С помощью коэффициента масштабирования a в декартовом пространстве изображение I(x,y) отображается на I(ax, ay). Чтобы определить коэффициент масштабирования в логарифмическом пространстве применим преобразование:
(x,y) ® (log x, log y), (ax, ay) ® (log ax, log ay),
(log ax, log ay) ® (log x + log a, log y + log a).
Становится очевидно, что в логарифмическом пространстве введение коэффициента масштабирования проявляется как изменение стадии в логарифмическом преобразовании изображения. Поэтому, вместо того, чтобы отображать изображение в координатное пространство (r,q), лучше отобразить его в координатное пространство (log r,q), используя логарифмически-полярное преобразование. Переводя начало координат оттранслированного изображения к центру в логарифмически-полярном пространстве, получают инвариантный коэффициент масштабирования в этом пространстве. Поэтому логарифмически-полярное преобразование — это инвариантное вращение и коэффициенты масштабирования первоначального изображения [3].
Дискретное преобразование Фурье
Дискретное преобразование Фурье для оттранслированного изображения эквивалентно дискретному преобразованию Фурье на первоначальном изображении. Поэтому можно применить дискретное преобразование Фурье на логарифмически-полярном изображении, преобразованном уравнением (15) и получить спектр его величин с помощью уравнения (16), где R (X) — вещественная часть, и I(X) — мнимая часть спектра Fourier.
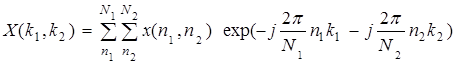 (15)
(15)
для 0 £ k1£ N1–1, 0 £ k1 £ N2 -1
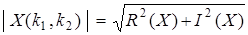 (16)
(16)
Теперь, мы можем получить инвариантные особенности изображения при преобразованиях Фурье-Меллина. Для этого, мы вычислим моменты спектра величин (дискретное преобразование Фурье), которые и будут особенностями инвариантов введения нейронной сети, можно также вычислить собственные значения и собственные векторы спектра Фурье (дискретное преобразование Фурье).
Преобразование Фурье-Меллина используется для идентификации образов которые подвергались некоторым преобразованием, таким как смещение, вращения, растяжение и сжатие.
Преобразование Фурье применяется для восстановления образов при сдвигах. Затем применяется логополярное преобразования для извлечения инвариантных признаков.
Алгоритм для извлечения инвариантных признаков
Шаг 1. Оцифровывание исходного образа.
Шаг 2. Трансформация образа такое как смещение, вращение, растяжение, сжатие.
Шаг 3. Применение преобразования Фурье-Меллина к каждому образу заключается в следующем
а) преобразование декартовых координат в полярные координаты используя лог-полярное преобразование для матрицы с размерностью (128´128) или (64´64) или (32´32).
б) применение быстрого преобразования Фурье для образов полярных координатах.
с) Вычисление абсолютного значения FFT которое выражает множество инвариантных признаков исходного образа.
д) Применение РСА метода для сокращения размерности вектора  .
.
Шаг 4. Использование множества базисных признаков найденных на шаге 3(д) в качестве входных данных для гибридной нейросети. В качестве инвариантного признаков берутся собственные значения в порядке возрастания.
Шаг 5. Применение гибридной сети к найденному на шаге и входному вектору  размерности 64 для сокращения размерности входного вектора и окончательное распознавания уже с помощью карты Кохенена.
размерности 64 для сокращения размерности входного вектора и окончательное распознавания уже с помощью карты Кохенена.
Заключение
Для решения исходной задачи производилось сравнение двух методов: метода геометрических моментов и метода преобразования Фурье-Меллина.
В результате сравнения определено что метод преобразования Фурье-Меллина предпочтительно для извлечения инвариантных признаков чем метод геометрических моментов, что дает и лучше качество распознавания. В свою очередь для метода преобразования Фурье-Меллина для сокращения размерности входного вектора удалось применить метод покомпонентного анализа (PCA) и было определено что 8 наибольших собственных значений дают лучшие результаты распознавания чем вектор  размерности 64.
размерности 64.
Литература:
1. Фролов А. А., Муравьев И. П. Нейронные модели ассоциативной памяти.- М.: Наука, 1987.- 160 ст.
2. Фу К. Структурные методы в распознавании образов.- М.: Мир, 1977.- 320 ст.
3. Фукунга К. Введение в статистическую теорию распознавания образов.- М.: Наука, 1982.- 367 ст.







