В настоящей работе сформулированы основные свойства числового образа линейного оператора в комплексном гильбертовом пространстве. Приведены несколько примеров разного характера для вычисления числового образа.
Ключевые слова: числовой образ, выпуклые множества, матрица, линейный оператор, точечный и аппроксимативно точечный спектры, ядро спектра, оператор левого сдвига, неравенство Коши-Буняковского.
1. Введение. Пусть 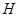 комплексное гильбертово пространство и
комплексное гильбертово пространство и 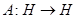 линейный оператор с областью определения
линейный оператор с областью определения 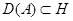 . Множество
. Множество
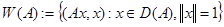
называется числовой образ оператора 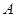 . Из определения видно, что множество
. Из определения видно, что множество 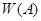 является подмножеством комплексной плоскости и геометрические свойства множества
является подмножеством комплексной плоскости и геометрические свойства множества 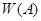 дает некоторые информации об операторе
дает некоторые информации об операторе 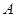 .
.
Изучение числового образа линейного оператора в гильбертовом пространстве является одним из основных методов при исследование местоположения спектра таких операторов. Это понятие впервые введено в работе [1] и доказано, что числовой образ матрицы содержит все ее собственные значения. В работе [2] показано, что числовой образ линейного оператора является выпуклым. Отметим, что выше сказанные результаты верны не только для матриц, но и в более общем случае для любого линейного ограниченного оператора. В работе [3] доказано, что спектр произвольного линейного ограниченного оператора содержится в замыкании числового образа этого оператора. Вслед за этим это понятие обобщено разными способами, см. например [4–6].
Числовой образ матриц хорошо изучены во многих работах, см. например [7,8]. В частности, в работе [7] доказано, что числовой образ матрицы 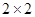 есть эллипс. Отметим, что [7] в случае, когда оператор является ограниченным и самосопряженным, замыкание числового образа есть выпуклая оболочка спектра.
есть эллипс. Отметим, что [7] в случае, когда оператор является ограниченным и самосопряженным, замыкание числового образа есть выпуклая оболочка спектра.
Данная работа посвящена изучению основных свойств числового образа линейного оператора. Вычислен числовой образ нескольких линейных операторов разного характера.
2. Основные свойства. В этом пункте ради удобства для читателей сформулируем некоторых свойств числового образа линейного оператора.
Пусть 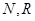 и
и 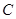 — множество натуральных, вещественных и комплексных чисел, соответственно. Обозначим через
— множество натуральных, вещественных и комплексных чисел, соответственно. Обозначим через 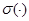 ,
, 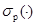 и
и 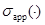 , соответственно, спектр, точечный спектр и аппроксимативно точечный спектр линейного оператора. Всюду в работе под
, соответственно, спектр, точечный спектр и аппроксимативно точечный спектр линейного оператора. Всюду в работе под 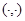 и
и 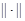 понимается скалярное произведение и норма в соответствующих гильбертовых пространствах.
понимается скалярное произведение и норма в соответствующих гильбертовых пространствах.
Свойства 1 (Теорема Тёплица-Хаусдорфа): Числовая образ линейного оператора есть выпуклая множества.
Свойства 2: 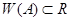 тогда и только тогда, когда
тогда и только тогда, когда 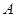 самосопряженный оператор.
самосопряженный оператор.
Свойства 3: Пусть 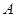 самосопряженный оператор и
самосопряженный оператор и 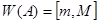 для некоторых
для некоторых 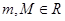 . Тогда имеет место равенство
. Тогда имеет место равенство 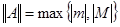 .
.
Свойства 4: Пусть 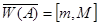 . Тогда
. Тогда 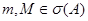 .
.
Свойства 5: Имеет место включение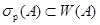 .
.
Определим (см. [8]) аппроксимативно точечный спектр линейного оператора 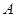 как
как
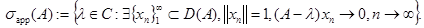
Подчеркнем, что последнее множество имеет еще одно название, «ядро спектра» 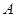 (см. [10]).
(см. [10]).
Следующее свойства устанавливает связь между 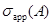 и
и 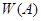 :
:
Свойства 6: Имеет место соотношение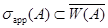 .
.
Следующий пример показывает, что даже для ограниченного самосопряженного оператора 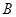 в гильбертовом пространстве
в гильбертовом пространстве 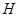 мы не сможем утверждать, что
мы не сможем утверждать, что 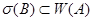 или
или 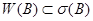 .
.
Пусть
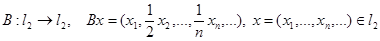 .
.
Легко проверяется, что
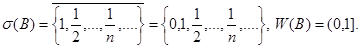
Остановимся, на доказательство факта 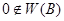 . Допустим противное. Пусть
. Допустим противное. Пусть 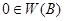 . Тогда существует
. Тогда существует 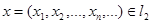 такое, что
такое, что 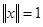 и
и 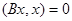 . Имеем
. Имеем
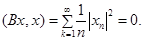
Отсюда следует, что 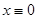 . Это противоречит факту
. Это противоречит факту 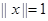 . Значить
. Значить 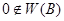 . Следовательно, в этом случае имеем
. Следовательно, в этом случае имеем 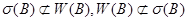 .
.
3. Примеры. В этом пункте рассмотрим некоторые примеры на вычисление числового образа линейного ограниченного оператора.
1. Пусть 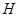 комплексное гильбертово пространство, а
комплексное гильбертово пространство, а 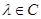 некоторое фиксированное комплексное число. Тогда для числового образа оператора
некоторое фиксированное комплексное число. Тогда для числового образа оператора 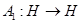 ,
, 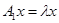 имеет место равенство
имеет место равенство 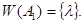
Действительно, если 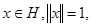 тогда
тогда 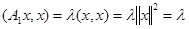 , т. е.
, т. е. 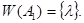
2. Вычислить числовой образ оператора 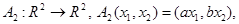 где
где 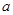 и
и 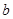 произвольные вещественные числа.
произвольные вещественные числа.
Возьмем произвольный элемент 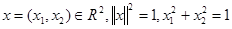 . Тогда
. Тогда 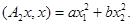 Если обозначить
Если обозначить 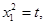 тогда
тогда 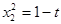 , где
, где 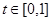 . Поэтому
. Поэтому
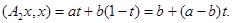
Так как 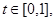 то
то 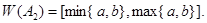
3. Вычислить числовой образ оператора 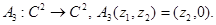
Возьмем произвольный элемент 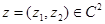 координаты которого удовлетворяют условию
координаты которого удовлетворяют условию 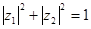 . Обозначим
. Обозначим 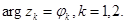 Тогда
Тогда 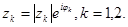 Теперь рассмотрим квадратную форму
Теперь рассмотрим квадратную форму 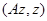 для элементов
для элементов 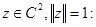
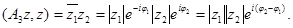
Здесь 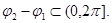 Если обозначить
Если обозначить 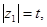 тогда
тогда 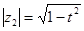 и
и 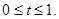 Поэтому
Поэтому
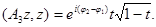
Видно, что когда 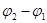 пробегает от
пробегает от  до
до 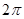 квадратная форма
квадратная форма 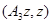 описывает окружность с центром в начале координат и с радиусом
описывает окружность с центром в начале координат и с радиусом 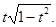 Тогда объединение таких окружностей по
Тогда объединение таких окружностей по 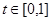 дает множество
дает множество 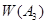 . Учитывая
. Учитывая 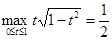 получим, что множество
получим, что множество 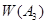 есть круг с центром в начале координат и с радиусом
есть круг с центром в начале координат и с радиусом 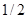 , т. е.
, т. е.
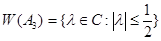 .
.
4. Числовой образ оператора 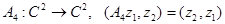 вычисляется как в примере 3 и верно
вычисляется как в примере 3 и верно 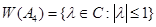 (вычислить самостоятельно).
(вычислить самостоятельно).
5. Покажем, что для числового образа оператора левого сдвига
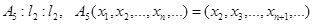
имеет место равенство 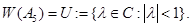
Очевидно, что для каждого 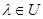 вектор
вектор 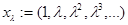 принадлежит в
принадлежит в 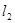 и
и 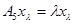 , т. е. каждое
, т. е. каждое 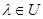 является собственным значением оператора
является собственным значением оператора 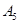 и соответствующий собственный вектор равно
и соответствующий собственный вектор равно 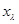 . Тогда
. Тогда 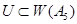 . Так как
. Так как 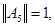 имеем
имеем 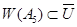 . Поэтому достаточно показать, что ни одна точка единичной окружности не лежит в
. Поэтому достаточно показать, что ни одна точка единичной окружности не лежит в 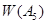 . Допустим противное, т. е. пусть некоторое комплексное число
. Допустим противное, т. е. пусть некоторое комплексное число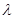 с модулью 1 лежат в
с модулью 1 лежат в 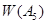 . Тогда существует элемент
. Тогда существует элемент 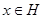 такое, что
такое, что 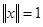 и
и 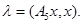 Так как
Так как 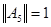 , согласно неравенству Коши-Буняковского имеет место соотношение
, согласно неравенству Коши-Буняковского имеет место соотношение 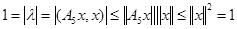 . Отсюда вытекает, что
. Отсюда вытекает, что 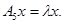 Легко можно проверить, что уравнению
Легко можно проверить, что уравнению 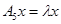 удовлетворяет только
удовлетворяет только 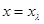 . С другой стороны
. С другой стороны 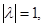 поэтому
поэтому 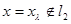 . Это противоречие показывает, что
. Это противоречие показывает, что 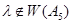 .
.
6. Пусть отображение 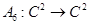 представляется в виде
представляется в виде
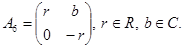
Допустим, что 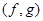 - единичный вектор в
- единичный вектор в 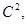 т. е.
т. е.
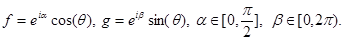
Тогда
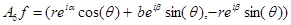
и
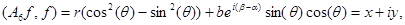
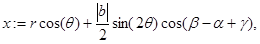
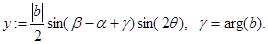
Таким образом
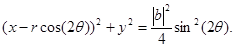
Последнее есть семейства окружностей, берем их объединение.
Перепишем последнее выражение в следующем виде
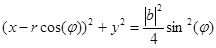 ,
, 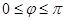
и дифференцируя по 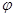 получим
получим
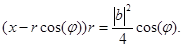
Из последних двух выражений получим
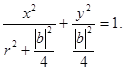
Это и есть эллипс.
Литература:
1. O. Toeplitz. Das algebraische Analogon zu einem Satze von Fejer // Math. Z. — 1918, — V. 2, — no. 1–2, — pp. 187–197.
2. F. Hausdorff. Der Wertvorrat einer Bilinearform // Math. Z. — 1919, — V. 3, — no. 1, — pp. 314–316.
3. A. Wintner. Zur Theorie der beschrankten Bilinearformen // Math. Z. — 1929, — V. 30, — no. 1, — pp. 228–281.
4. H. Langer, A. S. Markus, V. I. Matsaev, C. Tretter. A new concept for block operator matrices: the quadratic numerical range // Linear Algebra Appl. — 2001, — V. 330, — no. 1–3, — pp. 89–112.
5. C. Tretter, M. Wagenhofer. The block numerical range of an 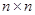 block operator matrix // SIAM J. Matrix Anal. Appl. — 2003, — V. 24, — no. 4, — pp. 1003–1017.
block operator matrix // SIAM J. Matrix Anal. Appl. — 2003, — V. 24, — no. 4, — pp. 1003–1017.
6. L. Rodman, I. M. Spitkovsky. Ratio numerical ranges of operators // Integr. Equ. Oper. Theory. — 2011, — V. 71, — pp. 245–257.
7. K. Gustafson, D. K. M. Rao. Numerical range: The field of values of linear operators and matrices. Berlin, Springer, 1997.
8. D. S. Keeler, L. Rodman, I. M. Spitkovsky. The numerical range of 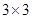 matrices // Linear Algebra and its Appl. — 1997, — V. 252, — no. 1–3, — pp. 115–139.
matrices // Linear Algebra and its Appl. — 1997, — V. 252, — no. 1–3, — pp. 115–139.
9. М. Рид, Б. Саймон. Методы современной математической физики. Т.4. Анализ операторов. М. Мир, 1982.
10. М. Саломяк, М. Бирман. Спектральная теория самосопряженных операторов в гильбертовом пространстве. Ленинград, Изд. Ленинградского университета, 1980.







