1. Введение. Одной из распространенных травм опорно-двигательного аппарата является перелом шейки бедра. В зависимости от его особенностей назначается консервативное (гипс) или оперативное лечение [1]. В последнем случае проводится остеосинтез при помощи различного вида фиксаторов. Довольно частым является применение трех спонгиозных винтов. Они представляют собой стержень (длиной 25-100 мм) с резьбовой частью (длиной 16-32 мм) диаметром 4,5-6,5 мм. Как правило, винты изготавливаются из титановых сплавов [1].
Математическая модель винтов построена на основе теории изгиба балок [2-4].
2. Анализ напряженно-деформированного состояния винта. Рассмотрим в декартовой системе координат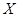 
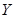
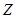балку длиной 
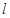с круговым сечением диаметра 
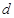, загруженную равномерно распределенной нагрузкой 
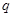(рис. 1).
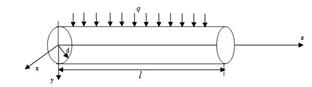
Рис. 1.
Дифференциальное уравнение изогнутой оси балки имеет вид [3]:
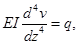(1)
где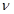 
— прогиб; 
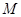— проекция изгибающего момента в точке 
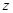на ось 
; 
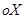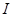- момент инерции площади поперечного сечения балки относительно его центральной оси, параллельной оси ; 
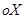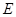— модуль Юнга.
Нормальное напряжение при изгибе выражается равенством [3]:
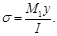(2)
Максимальные напряжения определяются по формуле [4]:
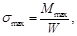(3)
где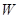 
— момент сопротивления сечения при изгибе.
Для кругового поперечного сечения
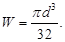(4)
В данной работе проводится исследование напряженно-деформированного состояния балки, защемленной на одном конце под действием равномерно-распределенной нагрузк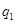и 
и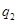 
(рис.2, рис.3).
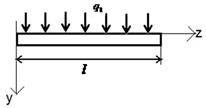
Рис. 2
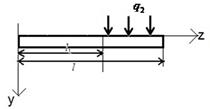
Рис. 3
Краевые условия имеют вид:
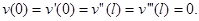(5)
Интегрируя уравнение (1), получаем функцию прогиба в первом случае:
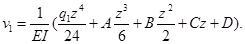
Принимая во внимание краевые условия (5), имеем
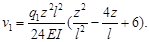
На основе формул (2) — (4) находим выражения для напряжения
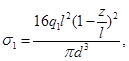
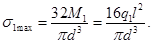(6)
Рассмотрим теперь балку, загруженную равномерно распределенной нагрузкой 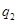на отрезке 
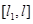(рис. 2). Этот случай особенно интересен, так как основная нагрузка приходится на головку бедра. Функции прогиба и напряжения могут быть найдены аналогичным способом, либо с помощью операционного метода [5]. Последний представлен ниже.
Дифференциальное уравнение изгиба балки в этом случае имеет вид:
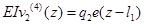, (7)
где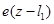 
— единичная функция или функция Хевисайда [6].
Применяя к уравнению (7) преобразование Лапласа [5], получим:
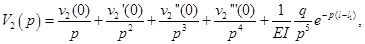
где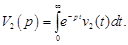 
Этому изображению соответствует оригинал
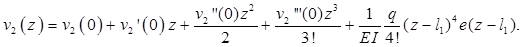
Учитывая краевые условия (5) и осуществляя необходимые преобразования, находим:
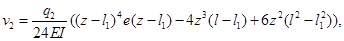
Напряжения, возникающие в сечении балки, будут определяться по формуле
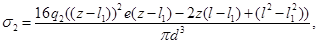
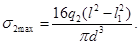
Проведем сравнительный анализ решений рассмотренных задач (рис.2, рис.3). Для этого введем функции: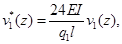 
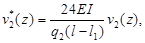
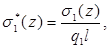
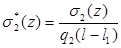. Полагая в них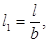 
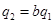, имеем
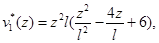
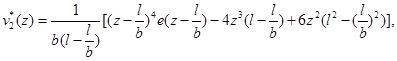
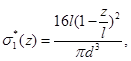
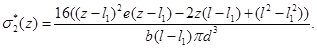
На рис. 4-6 представлены графики функций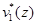 
, 
, 
, 
.
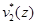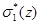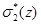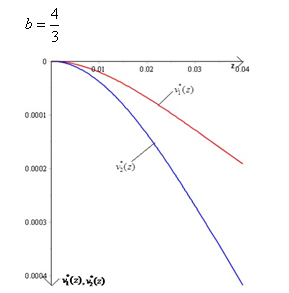
Рис. 4
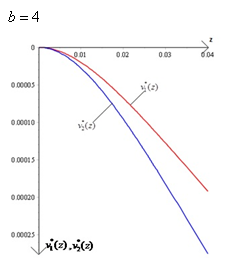
Рис. 5
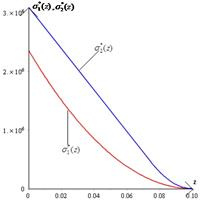
Рис. 6
Анализируя полученные результаты, можно заметить, что максимальные значения прогиба балки достигаются на ее конце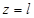 
, на противоположном (
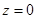) возникают наибольшие напряжения, причем их величины во втором случае (рис.3) больше, чем в первом (рис.2). При 
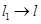различия между графиками функций уменьшаются, а при увеличении длины (диаметра винта) наблюдается рост (убывание) их значений.
3. Определение геометрических параметров винта в зависимости от нагрузки. Согласно Х.А.Янсону [7], показатели нагрузки на тазобедренный сустав в различных случаях составляют:
1) при опоре на обе ноги — 0,3P;
2) при опоре на оперированную ногу — 2,4P;
3) при передвижении в обычном темпе по ровной поверхности — 2P;
4) при подъеме и спуске по наклонной поверхности — 2,5P;
5) при быстрой ходьбе — 4,3P.
Здесь P — вес тела без опорной конечности.
Система бедро+голень+стопы составляет примерно 36 % массы человека [8].
Определим диаметр винта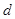 
, применяемого при фиксации вертельного перелома бедренной кости, исходя из характеристик материала. Наиболее предпочтительным для изготовления фиксаторов является титановый сплав 
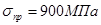[1].
В соответствии с формулой (6) для максимальных напряжений получаем:
, 
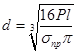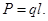
На рис.7 приведены графики зависимости диаметра винта 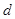от его длины 
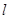в случаях 1-5:
Рис. 7
На основе полученных результатов следует отметить, что при фиксации вертельного перелома бедренной кости необходимо учитывать индивидуальные особенности пациента (различные типы нагрузки). При высокой активности или большой массе рекомендуется использовать винт большего диаметра.
Литература:
1. Анкин Л.Н., Анкин Н.Л. Травматология. Европейские стандарты. М.: Медэкспресс-информ, 2005. 496 с.
2. Папкович П.Ф. Труды по строительной механике корабля. Л.:Судпрогиз, Том 1, 1962. 576 с.
3. Короткин Я.И., Локшин А.З., Сиверс Н.Л. Изгиб и устойчивость стержней и стержневых систем (строительная механика корабля). М.: Машгиз, 1953. 517 с.
4. Беляев Н.М. Сопротивление материалов. М.:ФИЗМАТЛИТ, 1965. 856с.
5. Даль Ю.М. О решении некоторых дифференциальных уравнений механики операционным методом // Вестн. С.-Петербург. ун-та. Сер. 10. Прикладная математика. Информатика. Процессы управления, 2013, Вып. 4, С. 3–9
6. Лаврентьев М.А., Шабат Б.В. Методы теории функции комплексного переменного. М.:Наука, 1965. 737 с.
7. Янсон Х.А., Биомеханика нижней конечности человека. Рига: Зинатне, 1975. 324 с.
8. Дубровский В.И., Федорова В.Н. Биомеханика: учебник для средних и высших учебных заведений. М.:ВЛАДОС-ПРЕСС, 2003. 672 с.
