Одним из основных факторов, определяющих качество учебного процесса, является содержание и технология реализации образовательной программы как совокупности взаимоувязанных учебных курсов. Проектирование содержание учебного материала темы включает в себя следующие составляющие:
- определение целей обучения;
- формирование содержания темы;
- назначение технологий преподавания и освоения содержания темы;
- назначение технологий контроля (включая технологии самоконтроля) усвоения обучающимися учебного материала.
Неправильно спроектированная тема, курс не сможет обеспечить должное качество учебного процесса при самой блестящей его реализации.
Как известно, обучение предназначено дат ученику определенную сумму знаний, необходимый для его дальнейшей учебной деятельности. Конечной целью обучения является достижение обучаемым требуемого уровня знаний или степени обученности. Уровень знаний можно использовать в качестве критерия, характеризующего состояние обучаемой системы. В [1] предлагается, что обучающая система в процессе обучения проходит последовательно ряд промежуточных состояний α0, α1,… αi,…, αk, каждое из которых характеризуется определенным уровнем знаний z0, z1,… zi,… zk. Здесь z0 — исходный уровень знаний учащегося, z1, z2,… zk-1 — текущий уровень знаний учащегося; zк — рубежный, заключительный уровень знаний учащегося.
Что интересует сегодня ученика? Конечно же, это компьютер и современные технологии. Так почему бы нам не использовать это на своих уроках?
Для этого необходимо создать систему автоматизированных систем обучения и контроля знаний с использованием базы данных по предметам для индивидуализации обучения. При этом основной проблемой является структуризация содержания учебного материала на более мелкие учебные элементы (опорные понятия) [Шаталов] на основе логической граф схемы содержание темы предмета и их взаимосвязи.
Проблема структурирования и отбора содержания учебного материала давно и широко обсуждается. В настоящее время существует весьма много моделей логической структуризации учебного материала. Эти модели, несмотря на их разнородность в плане обоснования подходов и методов, прошли апробацию в реальном педагогическом процессе и дали свои положительные результаты.
Вопросу выяснения влияния логических связей (отношений) в учебном материале на дидактические свойства различных вариантов объяснения этого материала посвящена работа А. М. Сохора «Логическая структура учебного материала. Вопросы дидактического анализа» [2]. По его мнению, от того, что понимается под элементом учебного материала и от того, как устанавливаются связи между выделенными элементами, зависят и варианты представления логической структуры учебного материала.
Способом наглядного представления таких структур являются логические схемы. В этих схемах в качестве элементов знания выступают понятия, суждения, законы, важнейшие опыты. Эти элементы заключены в прямоугольники, они соединены стрелками в соответствии с последовательностью изложения учебного материала в учебнике. Фактически эти структурно-логические схемы являются ориентированными графами. В вершину графа помещаются структурные элементы изучаемого материала, а с помощью ребер изображаются связи элементов друг с другом. Поэтому с помощью графов можно наглядно представить структуру учебного материала.
А. В. Усова и В. А. Беликов [3] определяют следующие критерии выделения связей между элементами: а) наличие причинно-следственных отношений между элементами; б) наличие связи между основными, так называемыми родовыми понятиями, и их производными; в) функциональные связи между величинами; д) связь между элементами, один из которых входит в состав другого.
Учебный материал, который структурирован таким образом, бесспорно, при умелом использовании имеет ряд дидактических достоинств. Однако А. Н. Уман в работе, посвященной проблемам структурирования знаний и организации учебного материала [4], отмечает, что линейные структуры (знания, излагаемые в некоторой последовательности) одних и тех же знаний в различных учебниках и учебных пособиях даже по одному предмету не совпадают. Фактически линейных структур одного и того же материала столько, сколько существует учебников по данному предмету.
Положение усугубляется еще и в том случае, если подвергаемый структурированию учебный текст построен согласно принципу линейной систематичности. Согласно этому принципу, учебный материал представляет цепь элементов содержания, в которой предыдущее звено является основой для следующего. Кроме того, здесь существует также смысловая зависимость, благодаря которой каждый следующий элемент содержания зависит от предыдущего. Такое логическое построение темы, предмета в целом предъявляет к учащимся многие требования. Так как все элементы содержания темы понимаются здесь как равнозначные и ни один из них не выдвигается в качестве определяющего, то разграничение основного и производного содержания должно осуществляться самими учащимися. Не будучи способными к этому, они стараются овладеть всеми элементами содержания как равнозначными, без понимания положения каждого из них в целостной системе знаний. Это приводит зачастую к чисто механическому запоминанию знаний и к их цепному воспроизведению. В силу этого извлечение из последовательной цепи знаний одного из ее звеньев очень затруднено» [5].
При анализе и построении различных учебных текстов, выявлении и конструировании структур учебного материала неизбежно возникает вопрос об их оптимальности, принципах упорядочивания системы знаний. Так, Л. В. Занков при рассмотрении вопросов систематичности обучения в своем известном труде «Дидактика и жизнь» считает, что при решении данного вопроса на основе дидактических требований нельзя приходить в противоречие с системой и логикой соответствующей науки.
Говоря о логической структуре содержании учебного материала, способах его рационального изложения и усвоения, следует рассмотреть и теорию укрупнения дидактических единиц, автором которого является профессор П. М. Эрдниев [6]. В результате исследований им было показано, что решение проблемы интеграции знаний учащихся можно не упрощением заданий, а их усложнением — укрупнением дидактических единиц, — но при условии особой структуры учебного материала.
Из вышеизложенного можно сделать вывод, что состояние обучающей системы задаётся в виде логической структуры граф-дерево темы, предмета. Граф-дерево предмета имеет строго многоуровневую иерархическую структуру. Представляемый граф-дерево учебного материала темы, дисциплины содержит вершины преобразования информации, соответствующие дискретным режимам подачи порции учебного материала, вершины управления порциями учебного материала и вершины усвоения порции учебного материала. Используемый для целей управления познавательной деятельностью учащихся агрегированный граф является слабо связным, бес контурным и стохастическим в узлах преобразования, усвоения информации. Граф — дерево G учебного материала считается заданным, если известны: подмножество вершин 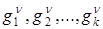 графа, соответствующее множеству К и уровням иерархии ν. Граф-дерево учебного материала темы, предмета имеет корневую вершину
графа, соответствующее множеству К и уровням иерархии ν. Граф-дерево учебного материала темы, предмета имеет корневую вершину 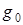 , промежуточные вершины
, промежуточные вершины 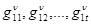 , соответствующие уровням иерархи и идентификации учебного материала, а также конечные вершины
, соответствующие уровням иерархи и идентификации учебного материала, а также конечные вершины 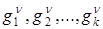 - опорные элементы, основные понятия которые подлежать к изучению, освоению, где ν — уровни иерархии.
- опорные элементы, основные понятия которые подлежать к изучению, освоению, где ν — уровни иерархии.
Уровень знаний может быть описан n-мерным вектором
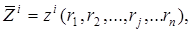
где r1, r2,…, rn — компоненты вектора, каждая из которых количественно выражает определенные свойства обучаемой системы, рейтинг ученика по опорным элементам темы, предмета в данный момент времени.
При изучении материала, который можно представить в виде дискретных приблизительно равных порций, степень обученности может характеризоваться статистической вероятностью определяемой как отношение числа усвоенных порций m к общему количеству преподносимых порций N, т. е. z = m/N.
Построение содержания темы, предмета в виде логической структуры учебного материала, отображается в дидактической модели усвоение знания о научном явлении, процессе и состоянии объекта. Но эта модель не является универсальной. Поэтому нами ставится следующая задача: получение и обоснование требований, которые позволят структурировать содержание учебного материала темы «Анализ квадратной функции» предмета Алгебра 9-класса с учетом категории сложностей математической формализации, алгоритмизации и программировании [7].
Сущность процесса структурирования состоит в том, чтобы выявить систему смысловых связей между элементами содержания дидактической единицы (учебной дисциплины, раздела, модуля, темы) и расположить учебный материал в той последовательности, которая вытекает из этой системы связей [3,4]. Вследствие этого процесс структуризации отвечает на вопросы: какова должна быть структура содержания темы и какова последовательность освоения элементов этого содержания? Применительно к структурированию содержания темы это означает выявление элементарных вопросов, учебных элементов, темы и последовательности их изучения в соответствии с логикой их взаимосвязи.
Для примера раскроем сущность структурирования учебного материала, в виде логического графа учебной информации. Логический граф учебной информации — это множество элементов содержания, построенных в определенных связях и отношениях. Он отражает выбранный преподавателем замысел построения и изложения учебного материала. В логическом графе учебной информации все его вершины (элементы) располагаются на горизонтальных линиях, каждая из которых соответствует выделенному основанию графа. Для построения сначала формируется спецификация оснований графа — перечень его оснований, представленных в соответствии с принятой преподавателем логикой изложения материала, а затем отбираются элементы графа.
Приведем пример из предмета Алгебра 9-класса глава 1 «Квадратной функции» с учетом категории сложностей математической формализации, алгоритмизации и программировании.
Спецификация логического графа темы, в виде опорных элементов, представлены на таблице.
|
Учебные вопросы |
Номер основания графа |
Учебные элементы. Наименование основных понятий |
|
|
Вопрос 1.1. Математическая формализация, алгоритмы, т. е. последовательности изучения (изложения) квадратной функции |
1.1.1 |
Понятие квадратной функции |
|
|
1.1.2 |
Применение квадратной функции в различных отраслях |
||
|
1.1.3 |
Разновидности квадратной функции |
||
|
1.1.4 |
|
||
|
1.1.4.1 |
|
||
|
1.1.4.2 |
|
||
|
1.1.4.3 |
|
||
|
1.1.4.3.1 |
Задание интервала изменения аргумента |
||
|
1.1.4.3.2 |
Выбор шага h изменения значение аргумента, и число точек N вычислений. |
||
|
1.1.4.3.3 |
Вычисление значения функции |
||
|
1.1.4.3.4 |
Построение графика функции |
||
|
1.1.4.3.5 |
Индивидуальные задания ученикам |
||
|
1.1.4.3.6 |
Проверка знаний учеников с помощью теста, задачи, словесный опрос |
||
|
1.1.5 |
|
||
|
1.1.5.1 |
|
||
|
1.1.5.2 |
|
||
|
1.1.5.3 |
|
||
|
1.1.5.3.1 |
Задание значения коэффициента а |
||
|
1.1.5.3.2 |
Задание интервала изменения аргумента |
||
|
1.1.5.3.3 |
Выбор шага h изменения значение аргумента, и число точек N вычислений. |
||
|
1.1.5.3.4 |
Вычисление значения функции |
||
|
1.1.5.3.5 |
Построение графика функции |
||
|
1.1.5.3.6 |
Анализ поведение функции |
||
|
1.1.5.3.7 |
Индивидуальные задания ученикам |
||
|
1.1.5.3.8 |
Проверка знаний учеников с помощью теста, задачи, словесный опрос |
||
|
|
1.1.6 |
|
|
|
1.1.6.1 |
|
||
|
1.1.6.2 |
|
||
|
1.1.6.3 |
|
||
|
1.1.6.3.1 |
Задание значении коэффициентов а,b,c |
||
|
1.1.6.3.2 |
Задание интервала изменения аргумента |
||
|
1.1.6.3.3 |
Выбор шага h изменения значение аргумента, и число точек N вычислений. |
||
|
1.1.6.3.4 |
Вычисление значения функции |
||
|
1.1.6.3.5 |
Построение графика функции |
||
|
1.1.6.3.6 |
Анализ поведение функции |
||
|
1.1.6.3.7 |
Индивидуальные задания ученикам |
||
|
1.1.6.3.8 |
Проверка знаний учеников с помощью теста, задачи, словесный опрос |
||
|
… |
… |
||
Логическая граф структура содержания главы 1 «Квадратные функции» представлена на рисунке 1.
Структурирование содержания учебного материала изменяет организацию учебного процесса, делает его более продуманным и диалектичным. Метод от простого к сложному, от теории к практике наиболее эффективен при исследовании устойчивых, стабильных, относительно закрытых реальных систем. Поэтому разработанные нами принципы структурирования учебного материала с учетом категории сложностей математической формализации, алгоритмизации и программировании задач позволяют сделать процессы структурирования доступным и методологически обеспеченным.
Для каждого учебного элемента подготавливается различные поясняющие словесные, графические материалы в виде презентаций, а также мультимедийных средств.
В разработанной нами методика структуризации главы 1 «Квадратные функции» предмета Алгебра для 9 класса на основе логической схемы, в экспериментальной проверке показала эффективность данной педагогической технологии обучения и продемонстрировала улучшение системных знаний учеников общеобразовательных школ, а также студентов начальных курсов профессиональных колледжа.
Создавая базы электронных ресурсов, на основе графосемантической структуры дисциплины, позволит не только повысить интерес учеников общеобразовательных школ к изучаемым дисциплинам, но позволит и самим преподавателям сохранить те бесценные наработки, которые имеются в арсенале любого преподавателя.

Рис.1. Логическая граф структура содержания главы 1 «Квадратные функции».
Подведя итоги проведения урока на основе структуризации темы, раздела, главы, предмета в целом можно сказать что:
- Уроки станут интереснее, т. к. благодаря смене видов активной деятельности изложения преподавателем содержание темы, урок становится более разнообразным;
- На уроках появится дисциплина за счет продуманности и наполнения каждого этапа, изучения учебных элементов. Учащимся просто некогда будет отвлекаться;
- Улучшается качество проверки знаний, т. к. теперь она будет максимально быстрой и объективной за счет использования компьютеризованных проверок знаний одновременно.
Современный урок в сочетании информационно-коммуникационной техники и педагогической технологии дает создавать продуктивные интересные уроки, повышается репутация современного учителя, появляется возможность работать творчески, целеустремленно, улучшается дисциплина на уроке, происходить наглядное и понятное обучение, появляется резерв времени, свободное время учителя, а также экономится сила и энергия учителя.
Литература:
1. Юсупов Ф., Раззаков Б. Оценка степени знаний студента (на примере предмета «информатика»).// Педагогик таълим. № 3. — Т.:, 2000.- 74–79 б.
2. Сохор А. М. Логическая структура учебного материала. Вопросы дидактического анализа. М.: Педагогика, 1974. — 192 с.
3. Юсупов Ф., Раззаков Б., Юсупов Д. Ф. Повышение эффективности изучения курса информатика на основе структурно-логической граф схемы дисциплины/Высшее образование сегодня. — М.: 2011, № 11. — С. 46–49.
4. Уман А. И. О структурировании знаний и организации заданий в учебном материале. // Проблемы школьного учебника. Вып. 12. (О специфике учебников математики, физики, астрономии, черчения и трудового обучения). — М.: Просвещение, 1983. — С. 15–28.
5. Сосницкий К. Построение содержания учебника // Проблемы школьного учебника. Вып. 3. (Структура учебника). — М.: Просвещение, 1975. — С. 18–29
6. Эрдниев П. М., Эрдниев Б. П. Укрупнение дидактических единиц в обучении математике.– М.: Просвещение, 1986. — 254 с.
7. Алгебра: Умумий ўрта таълим мактабларнинг 9-синфи учун дарслик/ Ш. А. Алимов, О. Р. Холмухамедов, М. А. Мирзаахмедов. — 2-нашри. — Т.: “Ўқитувчи” НМИУ, 2010. — 240 б.







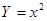 функция
функция
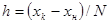
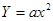 функция
функция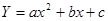 функция
функция