Оптимальное распределение нагрузок между станками драной системы маслоэкстракционного производства

В химической, пищевой, перерабатывающей промышленностях, энергетике и других отраслях часто используются системы, состоящие из параллельно включенных агрегатов, при этом повышается надежность системы, так как выход из строя части агрегатов не делает ее неработоспособной, кроме того, при переменных нагрузках отключение части агрегатов позволяет оставшимся работать в наиболее экономичном режиме [1].

Постановка задачи. Расходы сырья а_i, хлопковые семена, оптимально распределить между агрегатами драной системы (ДС) маслоэкстракционного производства так, чтобы общая производительность всех n агрегатов были максимальна при заданном расходе сырья на всю драную систему Q, при этом первоначально будем предполагать расходы сырья скалярными величинами, т. е. не учитывать, например его состав. Обозначения: a_i — нагрузочная характеристика i — го агрегата, т. е. интенсивность запуска сырья i –го агрегата ДС; Y_i=F(a_i) — зависимость производительности i — го агрегата от расхода сырья a_i. воспользуемся методикой изложенной в [2]. Будем считать, что режимные параметры агрегатов установлены, которые соответствует оптимальной производительности. Тогда задача оптимизации примет форму

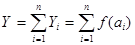                                                                                                     (1)

при условиях, наложенных на каждую из нагрузок,

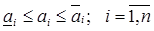                                                                                                (2)

и на их сумму 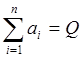                                                                                         (3)

Получается выпуклая задача распределения. Сделаем два важных допущения:

1.         Состав работающих агрегатов ДС определен, т. е. каждый агрегат включен и должен потреблять сырье не менее чем .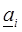

2.         нагрузочные характеристики агрегатов — выпуклые функции.

Первое допущение гарантирует выпуклость множества допустимых решений, так как условия (2) выделяют параллелепипед, а условия (3) — плоскость. Пересечение этих двух выпуклых множеств — выпукло. Второе допущение обеспечивает выпуклость целевой функции. Следовательно, в такой постановке задача распределения выпукла, и ее решение полностью определяется из необходимых условий оптимальности. Запишем эти условия [1]

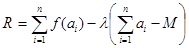                                                                                        (4)

Условия ее локальной не улучшаемости приводят к соотношениям

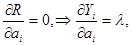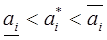
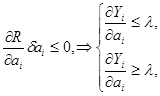 если

 если 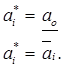                                                                  (5)

В свою очередь, величина 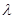должна обеспечить выполнение ограничения (3)

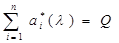
Пусть на основе обработки экспериментальных данных нагрузочная характеристика агрегата ДС описывается зависимостью,

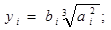
а ограничения (2) имеет вид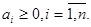

Сделаем допущение, что ни один из агрегатов ДС не выйдет на предельные значения расхода сырья. В этом случае используется только первые из условий (5). Из условий (4) имеем

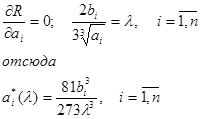
Подставляя эти выражения в условие (3), получаем

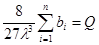
поэтому 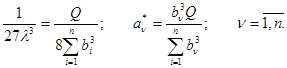                                                (6)

Оптимальная нагрузка каждого агрегата ДС пропорциональна заданной суммарной нагрузке и кубическому степени коэффициента 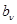 его нагрузочной характеристики.

если, нагрузочная характеристика агрегатов одинаковы т. е.

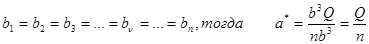                                           (6^’)

Рассмотрим случай несправедливости ранее сделанного допущения. На практике работы агрегатов ДС некоторые агрегаты могут работать при предельных нагрузках. Изложим алгоритм, предназначенный для расчета оптимального решения в этом случае.

Алгоритм последовательного назначения предельных нагрузок. Будем называть нагрузки, подсчитанных из условий стационарности функции Лагранжа без учета ограничений на а_i, стационарными и обозначать их как .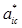

1-шаг. Отбрасываем в условиях задачи автономные ограничения (2) и рассчитываем стационарные нагрузки, после чего разбиваем все агрегаты ДС на три группы — недогруженные 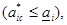 перегруженные  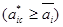и средние. Множество индексов недогруженных агрегатов будем обозначать через 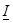, а перегруженных — через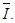

2-шаг. Подсчитываем суммарную перегрузку как разницу между суммой стационарных нагрузок и предельных нагрузок для перегруженных агрегатов.

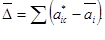
Аналогично рассчитываем суммарную недогрузку по всем недогруженным агрегатам.

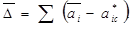
3-шаг. Возможны три случая:

a)                   если 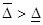, то оптимальные нагрузки перегруженных агрегатов следует назначить равными их предельным значениям

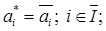
найти сумму этих нагрузок 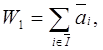 вычесть ее из Q и оставшуюся нагрузку (Q-W₁) распределяем между оставшимися агрегатами;

b)                  если 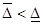, то оптимальные нагрузки недогруженных агрегатов следует принять минимально допустимыми  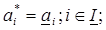и рассчитываем  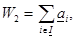а оставшуюся нагрузку (Q-W₂) распределяем между средними и перегруженными агрегатами;

c)                   если, наконец, 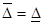, то всем перегруженным агрегатам назначаются максимальные 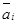, всем недогруженным — минимальные нагрузки 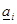, а средним агрегатам — рассчитанные для них стационарные нагрузки 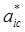. В этом последним случае задача считается решенной.

В случае а) и б) переходим к шагу 1 с меньшей суммарной нагрузкой и меньшим числом агрегатов. Так как после каждого цикла, число агрегатов, нагрузку которых не определены уменьшается хотя бы на единицу, то решение будет получено после конечного числа циклов, не превышающего n.

Обоснование алгоритма. Для доказательства оптимальности полученного решения нужно показать, что оно удовлетворяет условиям (5). Рассмотрим третий шаг алгоритма. В случае «а» из-за выпуклости наклоны характеристик перегруженных агрегатов для предельных нагрузок 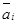 больше, чем наклоны этих же характеристик 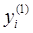для рассчитанных на первом шаге стационарных нагрузок; таким образом, эти наклоны больше значения  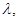найденного на первом шаге. При уточнении нагрузок оставшихся агрегатов величина 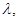может только уменьшиться, так как суммарная нагрузка на эти агрегаты увеличиться, по сравнению с суммой стационарных нагрузок. Таким образом, третье из неравенств (5) выполнено. В случае «б» совершенно аналогично можно показать, что для всех недогруженных агрегатов наклон их характеристик меньше чем наклон характеристик 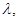у всех агрегатов, работающих при стационарных нагрузках, а значит, второе из условий (5) выполнено. Наконец, в случае «в» мы уменьшаем нагрузки перегруженных агрегатов по сравнению с рассчитанными для них стационарными (при этом наклон характеристик возрастает), увеличивается по сравнению с наклоном в точках  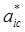для средних агрегатов). Таким образом, условий (5) выполнены.

В этой задаче имеется два типа переменных — 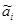 которые принимают любые значения в некотором диапазоне, и с_i, принимающие лишь целочисленные значения — нуль и единицу. Подобное оптимальные задачи называют частично целочисленными, и решается известными методами линейного или нелинейного программирования.

Реализации данного алгоритма рассмотрим на примере предыдущей задачи, с той разницей, что число агрегатов ДС зададим равным трем, величину Q=20:

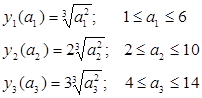
1-й цикл:

1-й шаг. По формулам (6) найдем стационарные нагрузки

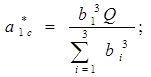
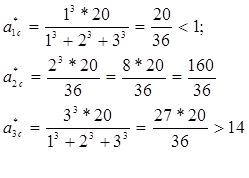
Таким образом, первый агрегат недогружен, а третий перегружен.

2-шаг. Недогрузка первого агрегата составляет

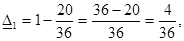 а перегрузка третьего агрегата

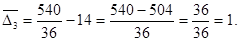
3-шаг. Так как 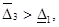 то назначаем предельную нагрузку перегруженному агрегату,  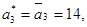а оставшуюся нагрузку  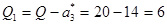распределяем между первым и вторым агрегатами.

2-цикл:

1-й шаг. Рассчитываем по формулам (6) стационарные нагрузки:

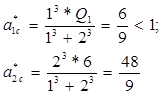
Таким образом, в данном случае недогрузка 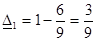, а перегрузка 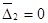. Поэтому 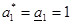. Оставшуюся нагрузку 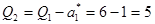. должен нести второй агрегат. Задача решена за два цикла, причем .

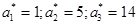Выбор состава действующего оборудования. Выше в задаче распределения нагрузок между параллельными агрегатами ДС предполагалось, что каждый из агрегатов работает хотя бы с минимальной нагрузкой. Если от этого требования отказаться и допустить возможность отключения агрегата, то множество решений для каждого i-го агрегата характеризуется условием

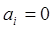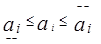 или                                                                                         (7)

Условия (7) удобно переписать, исключив слово «или», но введя добавочную переменную. Запишем а_i как произведение переменной 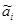, удовлетворяющей условию

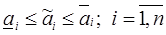                                                                                             (8)

n целочисленной переменной С_i принимающей значение 1, если i — агрегат включен в схему, и 0, если этот агрегат исключен.

Таким образом, 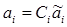 причем

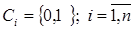                                                                                                     (9)

Условия (8) и (9) характеризует ограничения, наложенные на нагрузку каждого из агрегатов. Однако существует еще ограничения, наложенные на совокупность переменных.

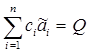                                                                                                                 (10)

Таким образом, формальная постановка задачи сводится к определению максимума суммарной производительности, которая с учетом введенных обозначений примет форму

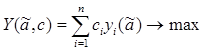                                                                                    (11)

при условиях(8), (9) и (10).

В этой задаче имеется два типа переменных — 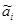 которые принимают любые значения в некотором диапазоне, и с_i, принимающие лишь целочисленные значения — нуль и единицу. Это последнее обстоятельство делает невозможной операцию дифференцирования по с, так как мы не можем варьировать эти переменные сколь угодно мало в окрестности их предполагаемого оптимального значения. Подобное оптимальные задачи называют частично целочисленными, и решается известными методами линейного и нелинейного программирования.

 

Литература:

 

1.                   Производственный технологический регламент на производство хлопкового масла и шрота по схеме форпрессование — экстракция на 2-х линиях МЭЗ-350 производительностью 800 т/сутки переработки семян хлопчатника. ТР 1602–28–2-02. Ташкент: МАСЛОЖИРТАБАКАПРОМ РУз., 2002.- 215 С.

2.                   Цирлин А. М. Оптимальное управление технологическими процессами. — М.: Энергоатомиздат, 1986. — 400 с.