На начальном этапе обучения в любом техническом высшем учебном заведении бакалавры и магистры получают фундаментальную подготовку, которая играет существенную роль в их дальнейшем профессиональном образовании. Глубокое изучение фундаментальных дисциплин позволяет создать прочную базу для подготовки специалиста, способного ориентироваться в непрерывно меняющейся производственной обстановке. В связи с этим остро встает вопрос усиления фундаментальной подготовки бакалавров и магистров, возникает необходимость в создании такой системы обучения, которая способствовала бы развитию теоретического и творческого мышления, формированию умений и навыков по ориентированию в стремительно растущем потоке научной информации.
Существенную роль в формировании профессионализма будущих специалистов может сыграть тесная междисциплинарная взаимосвязь. Использование во время учебных занятий статистических данных, собранных, например, в период производственной практики способствует более глубокому развитию экономического мышления и критического отношения к информации. В качестве примера использования междисциплинарных взаимосвязей в процессе обучения можно рассмотреть в виде регрессионного анализа при изучении дисциплины “ЭММиМ”.
Пример. По региону приведены данные стоимости кадастровых работ от площади земельного участка (таблица 1). Необходимо определить:
1. Уравнение парной регрессии y по x.
2. Рассчитать коэффициент парной корреляции, коэффициент детерминации.
Таблица 1
Данные стоимости заказа и площади земельного участка компании ООО «N» города N.
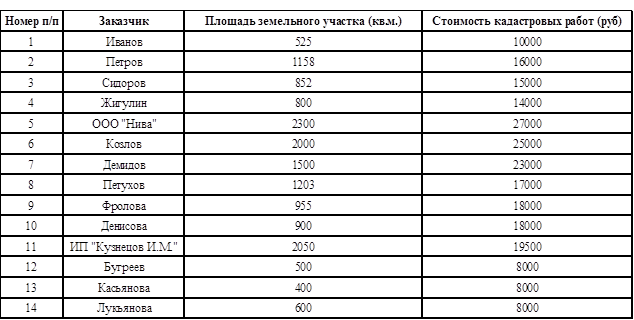
Наша цель — высчитать зависимость стоимости кадастровых работ от площади земельного участка. Для вычисления этой зависимости создадим таблицу из 14 заказчиков, площади земельного участка соответственно каждого заказчика и стоимости кадастровых работ за данный участок в программе Microsoft Office Excel.
В “Надстройках” выбираем “Пакет анализа” (рис.1).
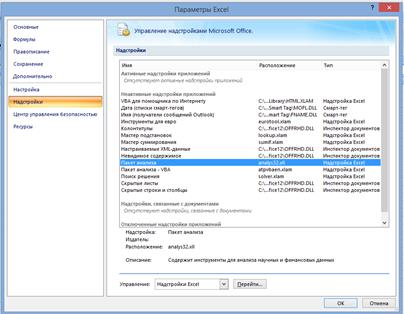
Рис.1
Далее (если исходные данные уже внесены), выбираем “Регрессия” (рис.2).
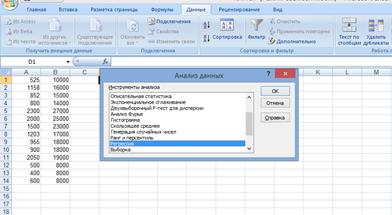
Рис.2
Заполняем диалоговое окно ввода данных и параметров вывода (рис.3).
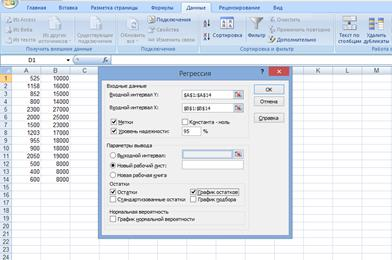
Рис.3
Получаем результаты расчета (рис.4):
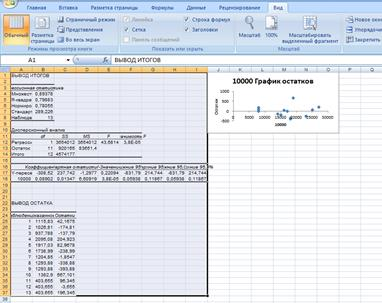
Рис.4
После построения модели естественным образом возникает вопрос о проверки адекватности выбранной модели. Одним из методов проверки адекватности является анализ остатков. Учитывая, что остатки попадают в горизонтальную полосу с центром на оси абсцисс, то выбранную модель можно признать адекватной.
С помощью инструмента анализа данных “Регрессия” получим уравнение прямой регрессии:
Yx=5940+9,0727x.
Коэффициент корреляции:
rxy=0,9022
Коэффициент детерминации:
r2xy=0,8140
(т. к. r2xy≥0,75, то модель может использоваться для прогнозов).
Литература:
1. Бочкарева, О. В. Математические задачи как средство формирования профессиональных качеств личности / О. В. Бочкарева, Т. Ю. Новичкова, О. В. Снежкина, Р. А. Ладин // Современные проблемы науки и образования.–2014.–№ 2; URL: www.science-education.ru/116–12584
2. Ладин, Р. А. Математика и междисциплинарные связи/Р. А. Ладин, О. В. Снежкина, О. В. Бочкарева, Н. В. Титова//Молодой ученый.- 2014.- № 1.- С. 550–552.
3. Бочкарева, О. В. Формирование профессиональных умений на занятиях по математике/ О. В. Бочкарева, О. В. Снежкина, М. А. Сироткина // Молодой ученый.- 2014.- № 2 (61).- С. 735–738.
4. Ладин, Р. А. Математика в учебном процессе строительного вуза/ Р. А. Ладин, О. В. Снежкина, Г. А. Левова //Вестник магистратуры.- 2013.- № 12–4 (27).- С. 56–59.
5. Сироткина, М. А. К вопросу о профессиональной направленности обучения математике / М. А. Сироткина, О. В. Бочкарева, О. В. Снежкина // Вестник магистратуры.- 2014.- № 2 (29).-С. 59–61.







