1. Постановка задачи
Начало исследованиям задачи Геллерстедта в своих трудах положил в 1937 году С. Геллерстедт [1]. Это было первым обобщением классического результата Ф. Трикоми [2]. Для уравнения
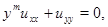
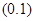
где 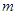 – натуральное нечетное число, в области
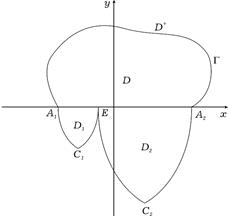
– натуральное нечетное число, в области  ограниченной простой кривой Жордана
ограниченной простой кривой Жордана 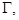 лежащей в полуплоскости
лежащей в полуплоскости 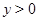 с концами в точках
с концами в точках 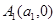 и
и 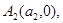 а при
а при 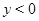 – характеристиками
– характеристиками 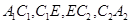 уравнения (0.1), где
уравнения (0.1), где 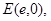
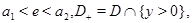
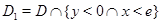 и
и 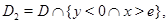 он исследовал краевые задачи с данными на
он исследовал краевые задачи с данными на 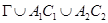 (задача
(задача 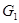 ) и с данными на
) и с данными на 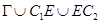 (задача
(задача 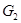 ). Существование упомянутых задач доказано методом интегральных уравнений в случае, когда
). Существование упомянутых задач доказано методом интегральных уравнений в случае, когда 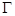 совпадает с "нормальной" кривой
совпадает с "нормальной" кривой 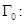
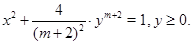 Для более общего уравнения
Для более общего уравнения
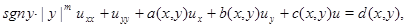 (0.2)
(0.2)
в [3] изучены аналоги задач  в классе обобщенных решений К.И.Бабенко, когда на эллиптической границе
в классе обобщенных решений К.И.Бабенко, когда на эллиптической границе  задано третье граничное условие. При этом существенными оказываются условия малости коэффициентов уравнения вблизи
задано третье граничное условие. При этом существенными оказываются условия малости коэффициентов уравнения вблизи 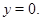 Относительно
Относительно 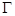 предполагаются выполненными известные условия К.И.Бабенко [4]. В совместной работе К.Б.Сабитова, А.Н.Кучкаровой [5] для одного уравнения смешанного типа вида (0.2) установлены принципы максимума решения задач
предполагаются выполненными известные условия К.И.Бабенко [4]. В совместной работе К.Б.Сабитова, А.Н.Кучкаровой [5] для одного уравнения смешанного типа вида (0.2) установлены принципы максимума решения задач 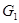 и
и 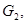 из которых следует единственность решений без каких-либо ограничений геометрического характера на эллиптическую границу области. Задача Геллерстедта для общих линейных систем уравнений смешанного типа рассматривалась лишь в работе [6]. В ней рассматривается система вида
из которых следует единственность решений без каких-либо ограничений геометрического характера на эллиптическую границу области. Задача Геллерстедта для общих линейных систем уравнений смешанного типа рассматривалась лишь в работе [6]. В ней рассматривается система вида
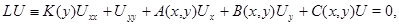 (0.3)
(0.3)
где 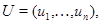
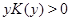 , при
, при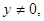
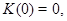
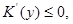
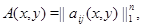
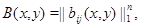
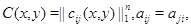
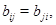 для всех
для всех 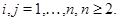 Методом "abc" при некоторых ограничениях на коэффициенты системы (0.3) и границу эллиптической части области доказана единственность решения
Методом "abc" при некоторых ограничениях на коэффициенты системы (0.3) и границу эллиптической части области доказана единственность решения 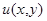 однородной задачи
однородной задачи 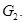 В работе К.Б.Сабитова [7] устанавливаются экстремальные свойства модуля
В работе К.Б.Сабитова [7] устанавливаются экстремальные свойства модуля 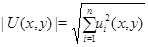 решения задачи Трикоми для системы уравнений смешанного типа (0.3), когда
решения задачи Трикоми для системы уравнений смешанного типа (0.3), когда 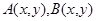 – числовые функции,
– числовые функции, 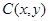 – квадратная матрица порядка
– квадратная матрица порядка 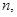 на основании которых следует единственность решения поставленной задачи без каких-либо ограничений на эллиптическую границу области и при более слабых условиях на коэффициенты системы. На основании этих результатов в статье К.Б.Сабитова, Р.Г.Идрисова [8] установлен принцип максимума модуля решения задачи Геллерстедта для системы уравнений смешанного типа (0.3), где
на основании которых следует единственность решения поставленной задачи без каких-либо ограничений на эллиптическую границу области и при более слабых условиях на коэффициенты системы. На основании этих результатов в статье К.Б.Сабитова, Р.Г.Идрисова [8] установлен принцип максимума модуля решения задачи Геллерстедта для системы уравнений смешанного типа (0.3), где 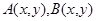 – числовые функции,
– числовые функции, 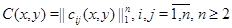 . В совместной работе К.Б.Сабитова, М.В.Мугафарова [9] устанавливаются экстремальные свойства решений задачи Трикоми, где под максимумом решения
. В совместной работе К.Б.Сабитова, М.В.Мугафарова [9] устанавливаются экстремальные свойства решений задачи Трикоми, где под максимумом решения 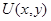 согласно [10] понимаетcя число
согласно [10] понимаетcя число 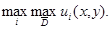 В данной работе идея, предложенная в [9], [8], реализуется для доказательства экстремальных свойств решения задачи Геллерстедта для системы уравнений смешанного типа.
В данной работе идея, предложенная в [9], [8], реализуется для доказательства экстремальных свойств решения задачи Геллерстедта для системы уравнений смешанного типа.
Рассмотрим систему
 где
где 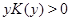 при
при 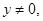
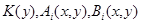 – заданные числовые функции,
– заданные числовые функции, 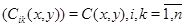 – квадратная матрица,
– квадратная матрица, 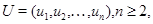 в области
в области 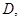 ограниченной простой кривой Жордана
ограниченной простой кривой Жордана 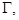 лежащей в полуплоскости
лежащей в полуплоскости 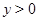 с концами в точках
с концами в точках 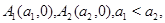 характеристиками
характеристиками 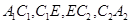 системы (1) при
системы (1) при 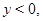 где
где 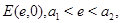
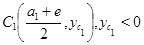 и
и 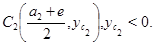 Пусть
Пусть 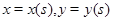 – параметрические уравнения кривой
– параметрические уравнения кривой 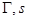 – длина дуги кривой, отсчитываемой от
– длина дуги кривой, отсчитываемой от 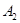 к
к 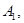
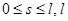 – длина кривой
– длина кривой 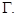 Обозначим через
Обозначим через 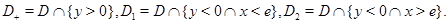 Будем предполагать, что
Будем предполагать, что
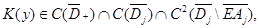
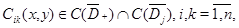
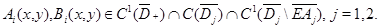
В областях 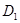 и
и 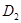 перейдем в характеристические координаты
перейдем в характеристические координаты 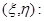
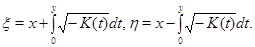 Тогда система (1) примет вид
Тогда система (1) примет вид
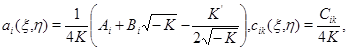
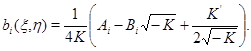
Область 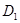 отобразится в
отобразится в 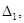 ограниченную отрезками
ограниченную отрезками 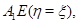
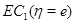 и
и 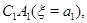 а область
а область 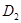 отобразится в
отобразится в 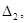 ограниченную отрезками
ограниченную отрезками 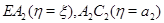 и
и 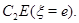 При этом за образами точек
При этом за образами точек 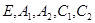 оставлены те же обозначения прообразов.
оставлены те же обозначения прообразов.
Для системы (1) в области 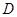 рассмотрим задачу Геллерстедта (задачу
рассмотрим задачу Геллерстедта (задачу  ).
).
Задача 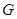 . Найти функцию
. Найти функцию 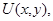 удовлетворяющую условиям
удовлетворяющую условиям
где 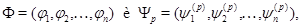
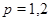 – заданные достаточно гладкие вектор-функции,
– заданные достаточно гладкие вектор-функции, 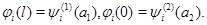
2. Экстремальные свойства решений системы в области эллиптичности
Лемма 1. Пусть 1) функция 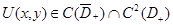 и
и 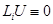 в
в 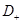 при всех
при всех 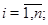 2) коэффициенты системы (1) в области
2) коэффициенты системы (1) в области 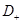 ограничены и
ограничены и
Тогда если 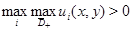
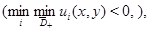 то этот максимум (минимум) достигается только на границе области
то этот максимум (минимум) достигается только на границе области 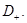
Доказательство. Пусть 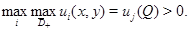 Допустим, что
Допустим, что 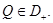 Тогда в точке
Тогда в точке 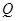
В силу условий (9) и (10) получаем
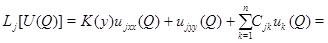
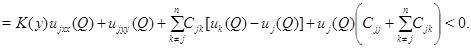
Но, с другой стороны, 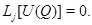 Полученное противоречие доказывает справедливость принципа максимума с условиями (9).
Полученное противоречие доказывает справедливость принципа максимума с условиями (9).
Лемма 2. Пусть 1) функция 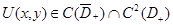 и
и 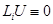 в
в 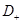 при всех
при всех 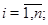 2) коэффициенты системы (1) в области
2) коэффициенты системы (1) в области 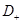 ограничены и
ограничены и
при этом функции 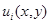 не равны постоянной в любой подобласти области
не равны постоянной в любой подобласти области 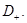 Тогда если
Тогда если 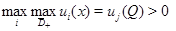
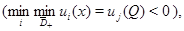 то этот максимум (минимум) достигается только на границе области
то этот максимум (минимум) достигается только на границе области 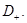
Доказательство. Введем вспомогательную функцию 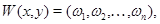 где
где 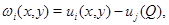 которая в области
которая в области 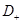 является решением системы
является решением системы
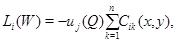
и 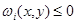 в
в 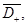
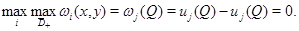 Значит, функция
Значит, функция 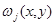 в
в 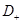 является решением эллиптического уравнения
является решением эллиптического уравнения
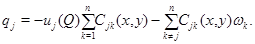
В силу условия (11) правая часть уравнения (12) неотрицательна в области 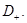 В самом деле,
В самом деле,
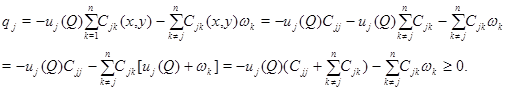
Пусть 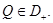 Поскольку оператор
Поскольку оператор 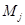 локально равномерно эллиптичен при
локально равномерно эллиптичен при 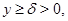 где
где 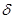 – достаточно малое число, и его коэффициенты в
– достаточно малое число, и его коэффициенты в 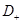 ограничены, то в силу теоремы Хопфа [11]
ограничены, то в силу теоремы Хопфа [11] 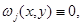 что невозможно. Значит,
что невозможно. Значит, 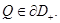
Лемма 3. Пусть 1) функция 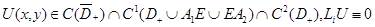 в
в 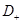 при
при 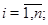 2) в области
2) в области 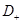 коэффициенты системы (1) ограничены и удовлетворяют условиям (11); 3)
коэффициенты системы (1) ограничены и удовлетворяют условиям (11); 3) 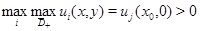
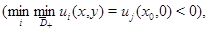
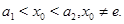 Тогда
Тогда
Доказательство. Пусть 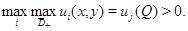 Рассуждая аналогично доказательству леммы 2, введем новую функцию
Рассуждая аналогично доказательству леммы 2, введем новую функцию 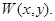 При этом функция
При этом функция 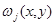 является решением эллиптического уравнения (12), правая часть которого в силу условия (11) в области
является решением эллиптического уравнения (12), правая часть которого в силу условия (11) в области 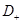 неотрицательна. Тогда коэффициенты уравнения (12) и функция
неотрицательна. Тогда коэффициенты уравнения (12) и функция 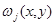 удовлетворяют условиям леммы 1 [12]. Поэтому
удовлетворяют условиям леммы 1 [12]. Поэтому 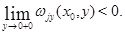 Отсюда уже следует неравенство (13).
Отсюда уже следует неравенство (13).
Лемма 4. Пусть 1) В области 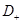 коэффициенты системы (1) ограничены и
коэффициенты системы (1) ограничены и
2) 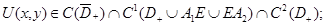 3)
3) 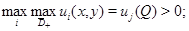 4) функция
4) функция 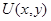 имеет изолированный положительный максимум
имеет изолированный положительный максимум 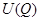 в точке
в точке 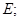 5) в малой окрестности точки
5) в малой окрестности точки 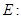 а) функция
а) функция 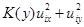 суммируема; б) производные
суммируема; б) производные 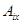 и
и 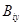 непрерывны вплоть до границы; в)
непрерывны вплоть до границы; в) 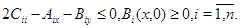 Тогда в любой выколотой окрестности
Тогда в любой выколотой окрестности 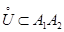 точки
точки 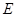 найдется точка
найдется точка 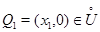 такая, что
такая, что
Доказательство. Пусть 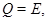 т.е.
т.е. 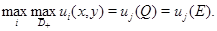 Допустим, что существует выколотая окрестность
Допустим, что существует выколотая окрестность 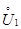 точки
точки 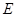 такая, что для всех
такая, что для всех 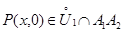 :
: 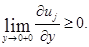 Введем вспомогательную функцию
Введем вспомогательную функцию 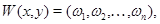 где
где 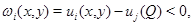 которая в области
которая в области 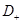 является решением системы
является решением системы
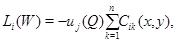 и
и 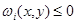 в
в 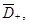
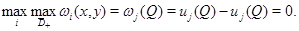 Значит, функция
Значит, функция 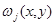 в
в  является решением эллиптического уравнения
является решением эллиптического уравнения
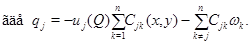 В силу условия (14) правая часть уравнения
В силу условия (14) правая часть уравнения 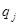 неотрицательна в области
неотрицательна в области 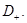 В самом деле,
В самом деле,
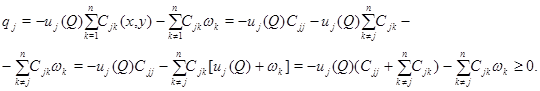
Пусть  Число
Число  возьмем настолько близким к числу
возьмем настолько близким к числу 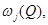 чтобы кривая
чтобы кривая 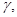 составленная из линии уровня
составленная из линии уровня 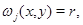 целиком лежала в
целиком лежала в 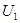 и для всех точек
и для всех точек 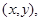 принадлежащих области
принадлежащих области 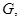 ограниченной кривой
ограниченной кривой 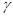 и отрезками
и отрезками 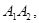
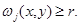 Поскольку
Поскольку 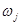 является в
является в 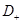 решением эллиптического уравнения
решением эллиптического уравнения 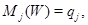 то в силу теоремы о представлении решений эллиптических уравнений следует существование такой кривой
то в силу теоремы о представлении решений эллиптических уравнений следует существование такой кривой 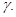 Причем, не теряя общности рассуждений, можно считать, что кривая
Причем, не теряя общности рассуждений, можно считать, что кривая 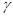 является спрямляемой. Обозначим через
является спрямляемой. Обозначим через 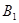 и
и 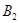 точки пересечения кривой
точки пересечения кривой 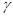 с отрезком
с отрезком 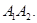
В области 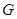 рассмотрим функцию
рассмотрим функцию 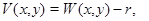 причем
причем 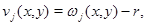 которая является решением эллиптического уравнения
которая является решением эллиптического уравнения
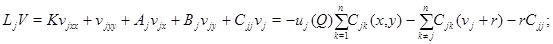
и удовлетворяют граничным условиям
Интегрируя тождество
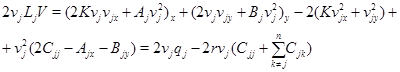
по области 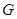 с учетом условий (17) и (18), получим
с учетом условий (17) и (18), получим
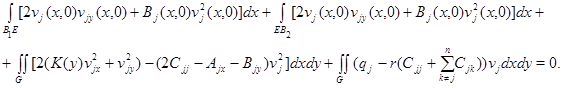
Из последнего равенства в силу наложенных на коэффициенты условий и неравенства (19), следует, что 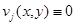 в
в 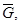 т.е.
т.е. 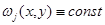 в
в 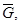 значит,
значит, 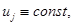 что противоречит условию изолированности максимума в точке
что противоречит условию изолированности максимума в точке 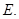 Следовательно, в любой окрестности
Следовательно, в любой окрестности 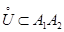 точки
точки 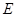 существует точка
существует точка 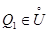 такая, что справедливо неравенство (15).
такая, что справедливо неравенство (15).
3. Экстремальные свойства решений системы в области гиперболичности
Рассмотрим систему (2) на множестве 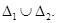 Пусть
Пусть 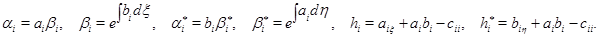
Функции 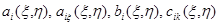 непрерывны в
непрерывны в  , кроме, быть может, отрезка
, кроме, быть может, отрезка 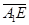 и удовлетворяют условию:
и удовлетворяют условию:
Функции 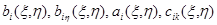 непрерывны в
непрерывны в 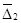 , кроме, быть может, отрезка
, кроме, быть может, отрезка 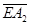 и удовлетворяют условию:
и удовлетворяют условию:
Определение 1. Регулярным в 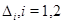 решением системы (2) назовем функцию
решением системы (2) назовем функцию 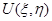 , удовлетворяющую условиям: 1)
, удовлетворяющую условиям: 1) 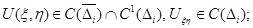 2)
2) 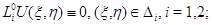 3) производная
3) производная 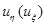 непрерывны на
непрерывны на 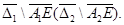
Лемма 5. Пусть: 1) коэффициенты системы (2) обладают отмеченной выше гладкостью и удовлетворяют условиям (21), (22); 2) 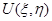 – регулярное в
– регулярное в 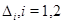 решение системы (2), равное нулю на
решение системы (2), равное нулю на 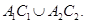 Тогда если
Тогда если 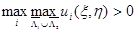 (
(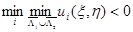 ), то этот максимум (минимум) достигается только на отрезке
), то этот максимум (минимум) достигается только на отрезке 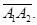
Доказательство. В области 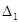 рассмотрим тождество
рассмотрим тождество
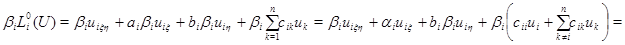
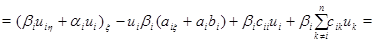
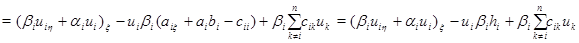
и проинтегрируем его по отрезку 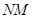 прямой
прямой 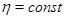 , принадлежащему
, принадлежащему 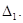 Тогда получим
Тогда получим
Пусть 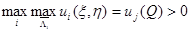 ,
, 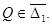 Ясно, что
Ясно, что 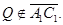 Пусть
Пусть 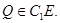 Из точки
Из точки 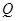 проведем отрезок
проведем отрезок 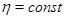 до пересечения с характеристикой
до пересечения с характеристикой 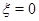 в точке
в точке 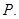 В равенстве (23) в качестве отрезка
В равенстве (23) в качестве отрезка 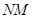 возьмем
возьмем 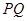 и положим
и положим 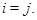 Тогда
Тогда
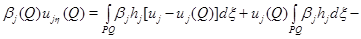
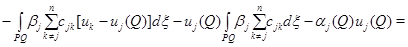
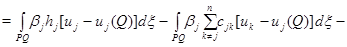
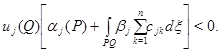
Последнее противоречит тому, что в точке 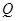 максимума функции
максимума функции 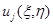 производная
производная 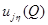 неотрицательна. Тогда
неотрицательна. Тогда 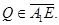 Аналогично, рассматривая область
Аналогично, рассматривая область 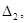 доказывается, что
доказывается, что 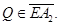
4. Экстремальные свойства решений системы в смешанной области
Рассмотрим систему (1) во всей смешанной области 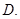
Определение 2. Регулярным в области 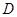 решением системы (1) назовем функцию
решением системы (1) назовем функцию 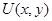 , удовлетворяющую условиям (3) – (5), и, кроме того, производные
, удовлетворяющую условиям (3) – (5), и, кроме того, производные 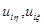 непрерывны на множествах
непрерывны на множествах 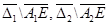 соответственно.
соответственно.
Теорема. Пусть: 1) коэффициенты системы (1) в области 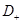 удовлетворяют условию 2) леммы 2; 2) выполнено условие 5) леммы 4; 3) коэффициенты системы (1) в областях
удовлетворяют условию 2) леммы 2; 2) выполнено условие 5) леммы 4; 3) коэффициенты системы (1) в областях 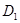 и
и 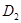 в характеристических координатах
в характеристических координатах 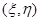 удовлетворяют, соответственно, условиям (21) или (22); 4)
удовлетворяют, соответственно, условиям (21) или (22); 4) 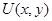 – регулярное в
– регулярное в 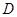 решение системы (1), равное нулю на характеристиках
решение системы (1), равное нулю на характеристиках 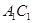 и
и 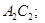 5)
5) 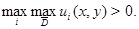 Тогда этот максимум достигается только на кривой
Тогда этот максимум достигается только на кривой 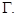
Доказательство. Пусть 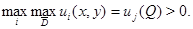 Так как выполнены условия леммы 5, то точка
Так как выполнены условия леммы 5, то точка 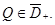 В силу леммы 1 точка
В силу леммы 1 точка 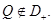 Тогда,
Тогда, 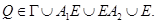 Пусть
Пусть 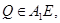 т.е.
т.е. 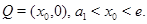 В этой точке из леммы 5 следует, что
В этой точке из леммы 5 следует, что 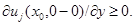 Последнее согласно лемме 3 противоречит неравенству
Последнее согласно лемме 3 противоречит неравенству 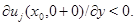 Если точка
Если точка 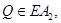 то рассуждая аналогично, получим противоречие. Следовательно,
то рассуждая аналогично, получим противоречие. Следовательно, 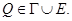 Пусть
Пусть 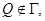 тогда
тогда 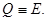 В этом случае
В этом случае 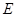 является единственной точкой изолированного глобального положительного максимума функции
является единственной точкой изолированного глобального положительного максимума функции 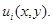 Линии уровня
Линии уровня 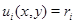 функции
функции 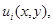 где
где 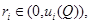 в малой окрестности точки
в малой окрестности точки 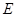 будут располагаться в области
будут располагаться в области 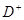 в виде концентрических линий вокруг точки
в виде концентрических линий вокруг точки 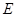 с концами
с концами 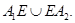 Докажем это. Допустим противное, т.е. в малой окрестности точки
Докажем это. Допустим противное, т.е. в малой окрестности точки 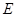 на оси
на оси 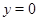 существуют точки
существуют точки 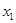 и
и 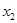 такие, что
такие, что 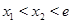 и
и 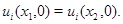 Тогда возможна линия уровня
Тогда возможна линия уровня 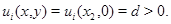 Функция
Функция 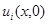 в некоторой точке
в некоторой точке 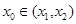 имеет положительный максимум
имеет положительный максимум 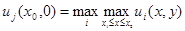 . Пусть
. Пусть 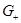 – область, ограниченная отрезком
– область, ограниченная отрезком 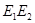 оси
оси 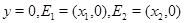 и линией уровня
и линией уровня 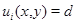 такая, что при всех
такая, что при всех 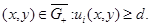 В силу принципа экстремума для эллиптических уравнений
В силу принципа экстремума для эллиптических уравнений 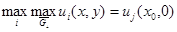 . Далее из точки
. Далее из точки 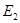 проведем характеристику системы (1) до пересечения с характеристикой
проведем характеристику системы (1) до пересечения с характеристикой 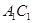 в точке
в точке 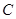 и рассмотрим область
и рассмотрим область 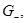 ограниченную линиями
ограниченную линиями 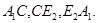 По лемме 5
По лемме 5 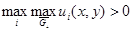 достигается на отрезке
достигается на отрезке 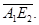 Не теряя общности рассуждений можно считать, что этот максимум достигается в точке
Не теряя общности рассуждений можно считать, что этот максимум достигается в точке 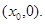 По лемме 3
По лемме 3 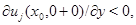 а с другой стороны на основании леммы 5
а с другой стороны на основании леммы 5 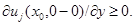 Получено противоречие. Отсюда следует, что в малой окрестности точки
Получено противоречие. Отсюда следует, что в малой окрестности точки 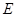 функция
функция 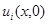 при
при 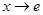 монотонно возрастает к значению
монотонно возрастает к значению 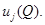 Пусть
Пусть 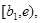 где
где 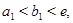 промежуток оси
промежуток оси 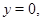 где
где 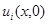 возрастает при
возрастает при 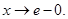 Покажем, что
Покажем, что 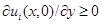 при всех
при всех 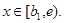 Пусть
Пусть 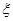 – любая точка из
– любая точка из 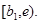 Из точки
Из точки 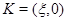 опустим перпендикуляр с концом в точке
опустим перпендикуляр с концом в точке 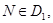 через точку
через точку 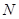 проведем характеристику системы (1) до пересечения с характеристикой
проведем характеристику системы (1) до пересечения с характеристикой 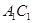 в точке
в точке 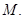 Обозначим через
Обозначим через 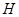 область, ограниченную характеристиками
область, ограниченную характеристиками 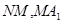 и отрезками
и отрезками 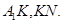 Аналогично лемме 5 можно показать, что
Аналогично лемме 5 можно показать, что 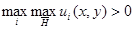 достигается только на отрезке
достигается только на отрезке 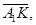 а именно в точке
а именно в точке 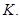 Тогда в этой точке
Тогда в этой точке 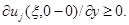 Следовательно, в силу произвольности точки
Следовательно, в силу произвольности точки 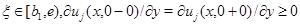 на
на 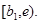 Аналогично показывается, что существует отрезок
Аналогично показывается, что существует отрезок 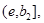 где
где 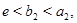 такой, что
такой, что 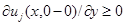 при всех
при всех 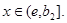 Тогда
Тогда 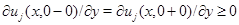 при всех
при всех 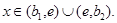 С другой стороны, в силу леммы 3 на
С другой стороны, в силу леммы 3 на 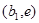 или на
или на 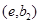 найдется точка
найдется точка 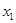 такая, что
такая, что 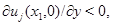 что противоречит неравенству
что противоречит неравенству 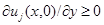 на
на 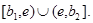 Следовательно, максимум не достигается в точке
Следовательно, максимум не достигается в точке 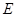 и точка
и точка 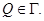
Следствие. а) Если выполнено условие теоремы, то для всех 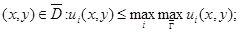 б) Если коэффициенты системы (1) удовлетворяют условиям теоремы и в классе регулярных в
б) Если коэффициенты системы (1) удовлетворяют условиям теоремы и в классе регулярных в 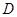 решений системы (1) существует решение задачи
решений системы (1) существует решение задачи 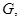 то оно единственно.
то оно единственно.
Литература
1. Gellerstedt S. Quelques problemes mixtes pour l'equation 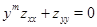 // Arkiv Mat., Astr. och Fysik. 3. 1938. B.26A. P.1-32.
// Arkiv Mat., Astr. och Fysik. 3. 1938. B.26A. P.1-32.
2. Трикоми Ф. О линейных уравнениях в частных производных второго порядка смешанного типа.Гостехиздат, 1947. 192 с.
3. Салахитдинов М.С., Исломов Б. Краевые задачи типа задачи Геллерстедта для общего линейного уравнения смешанного типа.// Изв. АН УзССР. Серия физ.-мат. наук. – 1986. – №2. – С.39-43.
4. Смирнов М.М. Уравнения смешанного типа. М.: Высшая школа. 1985. 304 с.
5. Сабитов К.Б., Кучкарова А.Н. О единственности решения задачи Геллерстедта для уравнений смешанного типа. /"Неклассические уравнения математической физики". Новосибирск. Изд-во ИМ СО РАН им. С.Л. Соболева. 2002. С. 206-220.
6. Овезова М.М. О единственности решения задачи Геллерстедта для общей системы уравнений Чаплыгина . // Докл. АН СССР. – 1996. – Т.348, – №1. – С. 25-26.
7. Сабитов К.Б. Экстремальные свойства модуля решений одного класса систем уравнений смешанного типа. // Докл. АН СССР. – 1990. – Т.310, – №1. – С. 33-36.
8. Сабитов К.Б., Идрисов Р.Г. Задача Геллерстедта для систем уравнений смешанного типа.// Изв. вузов. Математика. – 2001. – №11. – С.22-33.
9. Сабитов К.Б., Мугафаров М.Ф. К вопросу о существовании решения задачи Трикоми для одного класса систем уравнений смешанного типа. // Сиб. мат. журн. – 2002. – Т.43, – №3. – С.710-726.
10. Сабитов К.Б. Принцип максимума для систем уравнений смешанного типа второго порядка. // Докл. АН СССР. – 1989. – Т.305, – №4. – С. 783-786.
11. Hopf E.A. A remark on linear elliptic differetial equations of second order.//Proc. Amer. Math. Soc. – 1952. – V.3 – P. 791-793.
12. Сабитов К.Б. К вопросу о существовании решения задачи Трикоми// Дифференц. уравнения. – 1992. – Т.28,– 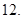 – C.2092 – 2101.
– C.2092 – 2101.







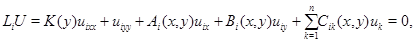 (
(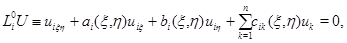 (
(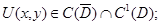 (
(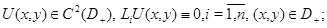 (
(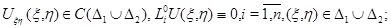 (
(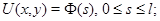 (
(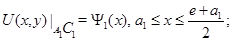 (
(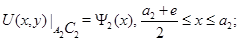 (
(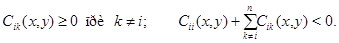 (
(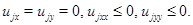 (
(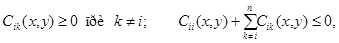 (
(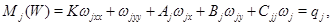 (
(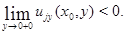 (
(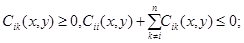 (
(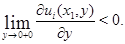 (
(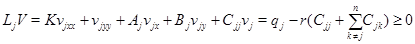 (
(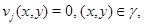 (
(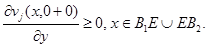 (
(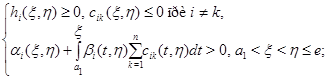 (
(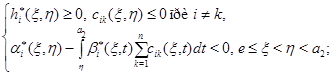 (
(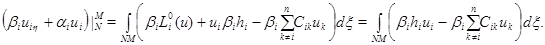 (
(