В плоскости Н введем прямоугольную правую систему координат хОу, неподвижную относительно рыхлительной лапы;
Обозначим через Ms текущую (т. е. имеющую криволинейную абсциссу s=s(t)) точку траектории L.
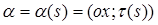
и рассмотрим направленный вертикально вниз единичный вектор g°. Он компланарен плоскости Н и допускает поэтому разложение по базису 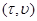 т. е. представим в виде
т. е. представим в виде
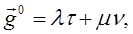 (1)
(1)
где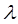 и
и 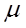 -его проекции на числовые оси, ортами которых служат
-его проекции на числовые оси, ортами которых служат 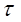 и
и 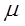 легко видеть, что (рис. 1)
легко видеть, что (рис. 1)
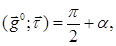
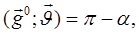
следовательно,
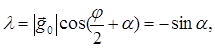 (2)
(2)
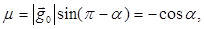 (3)
(3)
Из (1),(2),(3) следуют, что
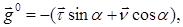 (4)
(4)
Значит
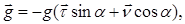 (5)
(5)
где g=9,81 м/с2. На основании (5) уравнение траектории почвенных частя
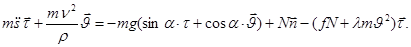 (6)
(6)
Траектория L почвенного комка, движение которого описывается уравнением (6), является геодезической линией поверхности S. Поэтому в каждой точке кривой L, т. е. в течение всего движения
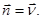 (7)
(7)
В силу (7), соотношение (6) обретает форму
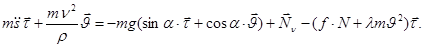 (8)
(8)
или, что то же,
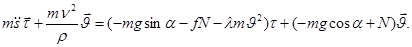 (9)
(9)
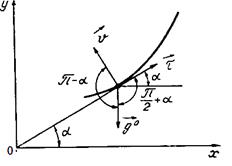
Рис. 1.
Ввиду неколлинеарности векторов 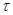 и
и 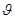 любое соотношение вида
любое соотношение вида 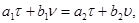 где
где 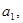
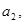
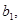
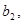 -скаляры, эквивалентно совокупности двух равенств
-скаляры, эквивалентно совокупности двух равенств
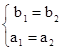
отсюда следует, что уравнение (10) равносильно (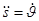 ) системе
) системе
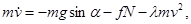 (10)
(10)
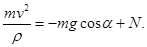 (11)
(11)
В ней 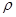 и
и 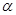 связаны соотношением
связаны соотношением 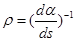
Поэтому полной системой дифференциальных уравнений, описывающих движение почвенной частицы по рабочей поверхности рыхлительной лапы, будет
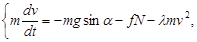 (12)
(12)
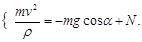 (13)
(13)
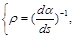 (14)
(14)
или
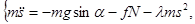 (15)
(15)
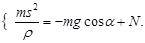 (16)
(16)
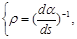 (17)
(17)
где 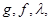 m= const > 0
m= const > 0
Система (12), (14) (или, что равносильно, (15–16) состоит из трех независимых друг от друга уравнений, содержащих четыре функции, следовательно, если одна из них задана, то остальные три могут быть определены. Выбор задаваемой функции зависит от проблемы, для исследования которой будут использованы соотношения (12–14).







