Процесс информатизации образования в Казахстане предполагает широкое внедрение компьютерных технологий в учебный процесс. Применение новых информационных технологий в учебном процессе позволяет повысить не только эффективность, но и качество подготовки специалистов [1]. При подготовке специалистов высшей квалификации по специальности «Математическое и компьютерное моделирование» изучение разностных методов решения уравнений в частных производных, является очень важной частью курса «Численные методы математической физики». Автоматизация решения задач данного типа во много раз ускорит учебный процесс и позволит студентам приобрести навыки математического и компьютерного моделирования различных физических процессов.
Авторами была разработана программа, которая позволяет автоматизировать процесс вычисления решения одной разностной задачи для волнового уравнения. Программа предназначена для освоения студентами разностного метода решения уравнений гиперболического типа и может применяться в учебном процессе.
В данной работе рассматривается проблема построения явной разностной схемы. Основная идея состоит в том, что после замены дифференциального уравнения гиперболического типа его конечно-разностной аппроксимацией получаются формулы, явно выражающие значения решения для одного расчетного временного слоя через значения решения на предыдущем временном слое. Таким образом, если известно решение в начальный момент времени, можно шаг за шагом (по слоям) найти решение для всех последующих моментов.
Постановка задачи [2]. Построить явную разностную схему для решения задачи, в которой имеется струна длиной 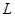 , натянутая между двумя точками оси
, натянутая между двумя точками оси 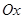 , точкой
, точкой 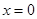 и точкой
и точкой 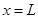 . Концы струны закреплены, начальное смещение струны описывается функцией
. Концы струны закреплены, начальное смещение струны описывается функцией 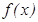 , а начальная скорость – функцией
, а начальная скорость – функцией 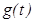 .
.
Решается первая начально-краевая задача для волнового уравнения
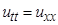 ,
,  ,
, 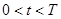 , (1)
, (1)
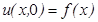 ,
, 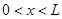 , (начальное условие)
, (начальное условие)
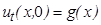 ,
, 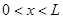 , (начальное условие)
, (начальное условие)
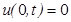 ,
, 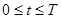 , (краевое условие на левой границе)
, (краевое условие на левой границе)
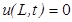 ,
, 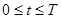 , (краевое условие на правой границе)
, (краевое условие на правой границе)
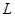 ,
, 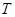 - заданные числа.
- заданные числа.
Требуется найти функцию 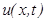 , которая удовлетворяет дифференциальному уравнению (1) в области
, которая удовлетворяет дифференциальному уравнению (1) в области 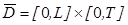 и соответствующим условиям на ее границе.
и соответствующим условиям на ее границе.
Для аппроксимации производных в рассматриваемом уравнении используются центральные разностные производные второго порядка по времени 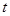 и по пространственной переменной
и по пространственной переменной 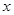 :
:
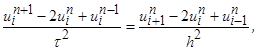
где 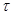 - шаг по времени
- шаг по времени 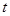 и
и 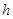 - шаг по пространственной переменной
- шаг по пространственной переменной 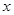
Отсюда
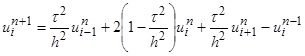 ,
,  . (2)
. (2)
Эта формула при фиксированном значении  выражает решение на
выражает решение на  -м временном слое через решение на
-м временном слое через решение на 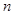 -м и
-м и 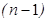 -м слое. В отличие от схем для уравнения теплопроводности, в которых использовались только два временных слоя (
-м слое. В отличие от схем для уравнения теплопроводности, в которых использовались только два временных слоя (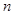 -й и
-й и 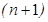 -й), здесь требуется использовать три слоя:
-й), здесь требуется использовать три слоя: 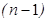 -й,
-й, 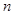 -й и
-й и 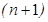 -й. Ей соответствует пятиточечный шаблон, который называется схемой «крест».
-й. Ей соответствует пятиточечный шаблон, который называется схемой «крест».
При записи в разностной форме начальное условие 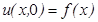 ,
, 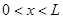 , запишется в следующем виде:
, запишется в следующем виде:
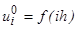 ,
, 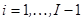 , (3)
, (3)
начальное условие 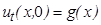 ,
, 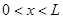 , применением правой разностной производной при
, применением правой разностной производной при 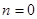 запишется в виде
запишется в виде 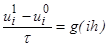 ,
, 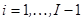 , или, используя соотношение (3), получим
, или, используя соотношение (3), получим
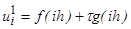 ,
, 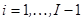 , (4)
, (4)
краевые условия представляются в форме:
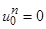 ,
, 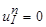 ,
, 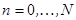 . (5)
. (5)
Соотношения (2)-(5) образуют явную трехслойную разностную схему. Эта схема имеет первый порядок аппроксимации по 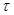 и второй – по
и второй – по 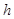 , так как соотношение (4) аппроксимирует дифференциальное начальное условие с первым порядком. Данная схема условно устойчива (устойчива при выполнении условия
, так как соотношение (4) аппроксимирует дифференциальное начальное условие с первым порядком. Данная схема условно устойчива (устойчива при выполнении условия 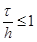 ).
).
Алгоритм вычислений по явной схеме.
1. Задать значения шагов сетки 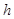 ,
, 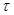 так, что
так, что 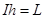 ,
, 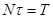 , где
, где 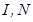 - целые положительные числа, причем значение шага по времени выбрать из условия устойчивости
- целые положительные числа, причем значение шага по времени выбрать из условия устойчивости 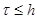 . Вычислить
. Вычислить
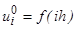 ,
, 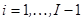 ;
; 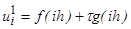 ,
, 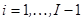 ,
,
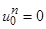 ,
, 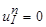 ,
, 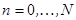 .
.
Приведенные выражения дают решение задачи для двух первых слоев сетки. Положить 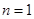 .
.
2. Найти решение на 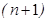 -м временном слое:
-м временном слое:
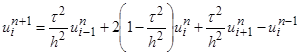 ,
, 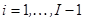 .
.
3. Если 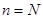 , вычисления завершить. Иначе положить
, вычисления завершить. Иначе положить 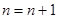 и перейти к п. 2.
и перейти к п. 2.
Пример. Пользуясь явной схемой, найти приближенное решение первой начально-краевой задачи:
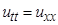 ,
, 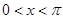 ,
, 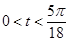 ,
,
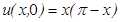 ,
, 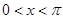 , (начальное условие)
, (начальное условие)
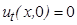 ,
, 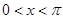 , (начальное условие)
, (начальное условие)
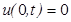 ,
, 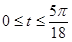 , (краевое условие на левой границе)
, (краевое условие на левой границе)
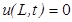 ,
, 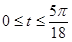 , (краевое условие на правой границе)
, (краевое условие на правой границе)
Решение. Сравнивая с общей постановкой задачи, получаем 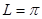 ,
, 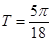 .
.
1. Зададим шаг по пространству равным 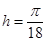 , шаг по времени выберем из условия устойчивости:
, шаг по времени выберем из условия устойчивости: 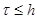 . Положим
. Положим 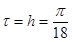 . Тогда
. Тогда 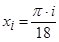 ,
, 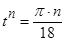 ,
, 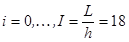 ;
; 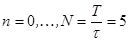 .
.
По формулам (3), (5), (6), учитывая, что 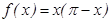 ,
, 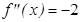 ,
, 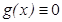 , получаем значения приближенного решения на нулевом и первом слоях:
, получаем значения приближенного решения на нулевом и первом слоях:
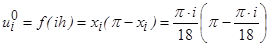 ,
, 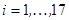 ,
,
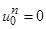 ,
, 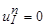 ,
, 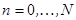 .
.
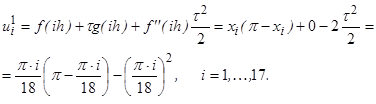
2, 3. Поскольку 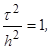 решение на последующих слоях вычисляется по формуле, вытекающей из (2):
решение на последующих слоях вычисляется по формуле, вытекающей из (2): 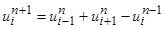 ,
, 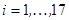 .
.
Для численной реализации данного алгоритма была выбрана среда разработки Borland Delphi 7, так как данный язык программирования обладает достаточным функционалом для решения рассматриваемой задачи. В среде Delphi 7 имеются обширные библиотеки программ для решения математических задач. При разработке программы для поставленной задачи был использован Анализатор – написанный вручную модуль для среды программирования Delphi 7. Основной задачей Анализатора является определение введенной математической функции в поле Edit. Модуль сравнивает заложенные в него значения с введенными значениями в Edit и выводит результат. Данный модуль был написан в связи с тем, что поле ввода Edit имеет тип – строковый, а математическая функция не является каким-либо типом. Применение Анализатора позволило вводить начальные и краевые условия с произвольными математическими функциями и позволило значительно сократить код основной программы. На рисунке 1 представлен интерфейс программы.

Рис. 1. Интерфейс программы
Предварительный расчет предназначен для проверки входных данных и условия усточивости 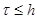 разностной схемы. Расчет первого этапа вычисляет значения искомого решения разностной задачи на 0-м и 1-м слое, при этом используются начальные и граничные условия. Расчет второго этапа выдает результат применения схемы «крест» для вычисления значений решения на 2-м слое.
разностной схемы. Расчет первого этапа вычисляет значения искомого решения разностной задачи на 0-м и 1-м слое, при этом используются начальные и граничные условия. Расчет второго этапа выдает результат применения схемы «крест» для вычисления значений решения на 2-м слое.
Результат программы для приведенного выше тестового примера представлен на рисунке 2. Решение волнового уравнения при заданных начальных и краевых условиях представлено в виде таблицы значений в узлах построенной сетки.
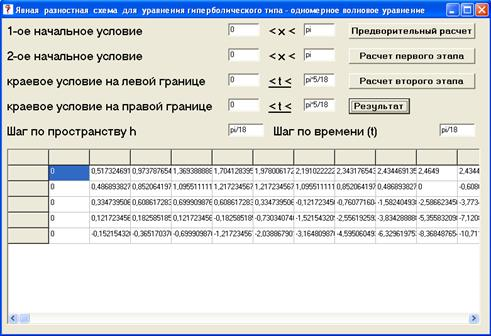
Рис. 2. Вывод результата
Программа позволяет задавать произвольные границы прямоугольной области, начальные и краевые условия для поставленной задачи, а также шаги по времени и по пространственной переменной (не нарушая условия устойчивости). Так как программа рассчитана не только на пользователя, обладающего навыками программиста, ее интерфейс максимально упрощен.
Литература:
1. Тaлызинa Н.Ф. Метoдикa cocтaвления oбучaющих пpoгpaмм. – М.: МГУ, 1980. - 260 c.
2. Киреев В. И. Численные методы в примерах и задачах: учеб. пособие/ В. И. Киреев, А. В. Пантелеев. - Изд. 2-е, стер. - М.: Высшая школа, 2006. - 480 с.
3. Хавьер Пашеку. Программирование в Borland Delphi 2006 для профессионалов. Delphi for .NET Developer’s Guide. - М.: Вильямс, 2006. - 944 с.







