Первоочередной задачей начального курса математики современные педагогики называют формирование вычислительных навыков. Этот раздел школьной математики всегда определялся как приоритетный при формировании математических знаний младших школьников. В современных учебниках содержательную основу начального математического образования оставляют понятия числа и четырех арифметических действий. В настоящее время система образования должна формировать такие новые качества личности выпускника как инициативность, инновационность, мобильность, гибкость, динамизм и конструктивность [1, с. 46], что особенно относится и к умению выпускника начальной школы быстро и правильно считать.
Существующие программы по математике начальной школы содержат объемный разнообразный материал по формированию осознанных навыков вычислений, однако, до сих пор отдельные вопросы восприятия и отработки навыка арифметических вычислений остаются для учащихся достаточно трудными.
Вычислять точно и быстро, подчас на ходу, — это основной залог успешного обучения в средней школе. Не умея вычислять, нельзя добиться успеха как в повседневной жизни, так и во время обучения. Уметь быстро, точно, правильно выполнять вычисления необходимо уже в начальной школе как для продолжающейся работы с числами, так и для дальнейшего обучения. В связи с этим, формирование у учащихся прочных вычислительных навыков по-прежнему является серьезной педагогической проблемой.
Известно, что у школьников с выработанными вычислительными навыками во много раз меньше трудностей при дальнейшем изучении математики. Но для того чтобы научиться правильно считать, быстро выполнять простейшие преобразования, необходимо уделять время на каждом уроке математики. Как показывает практика, 5–10 минут устного счета, включенного в начало урока малоэффективны не только для развития вычислительных навыков, но даже и для их закрепления. Должна существовать система устного счета. Устные упражнения должны применяться во всех подходящих случаях не только на «небольших числах», но и распространяться на удобные для устного счета задания в процессе всего начального обучения. Задача учителя состоит в том, чтобы найти максимум педагогических ситуации, в которых ученик стремились бы производить в уме арифметические действия.
Учащиеся не всегда способны активно использовать знания, умения, навыки в практической деятельности, адекватно воспринимать учебные задачи, уметь быстро находить пути их решения, преодолевать учебные проблемы, поставленные перед ними учителем [2, с. 91]. Очевидно, что фундамент развития вычислительных умений и навыков должен закладываться в курсе математики начальной школы. Формирование вычислительных навыков является приоритетной задачей начального математического образования [3, с. 139]. Именно в 1–2 классах закладываются основы обучения математике. Если не научить детей считать в этот период, в дальнейшем они будут постоянно испытывать различные трудности при выполнении вычислений.
Проблема формирования у учащихся вычислительных умений и навыков всегда привлекала особое внимание психологов, дидактов, методистов, учителей. В методике математики известны исследования Е.С Дубинчук, А. А. Столяра, С. С. Минаевой, Н. Л. Стефановой, Я. Ф. Чекмарева, М. А. Бантовой, М. И. Моро, Н. Б. Истоминой, С. Е. Царевой и др. Исследования большинства из них посвящены преимущественно разработке качеств вычислительных навыков (М. А. Бантова), рационализации вычислительных приемов (М. И. Моро, С. В. Степанова и др.), применению средств ТСО (В. И. Кузнецов), дифференциации и индивидуализации процесса формирования вычислительных умений и навыков (Т. И. Фадейчева).
Каждое из этих исследований внесло определенный вклад в разработку и совершенствование той методической системы, которая использовалась в практике обучения, и нашло отражение в учебниках математики.
В соответствии с действующими учебниками по математике для начальной школы рассмотрение вычислительного приема осуществляется только после того, как учащиеся осознают его теоретическую основу (определения арифметических действий, свойства действий и следствия, вытекающие из них). Отметим, что в каждом конкретном случае младшие школьники уясняют сам факт использования соответствующих теоретических положений, лежащих в основе вычислительного приема, конструируют различные приемы для одного случая вычислений, используя различные теоретические положения. Начальный курс математики основывается на такой последовательности введения вычислительных приемов, при которой вводятся постепенно, наращивая большее число операций. А приемы, усвоенные ранее, включаются в новые в качестве основных операций.
Учебники математики ориентированы на общие вычислительные навыки, и учитель может легко обучить алгоритму вычислений. Но в учебниках, к сожалению, нет «отработки частных способов вычислений», равно как нет и общих способов [4, с. 139].
Отмечается ухудшение качества вычислений учащихся, обучающихся по всем существующим программам. Особенно пострадала культура устного счета. Стремление учителей изменить ситуацию приводит к тому, что одни учителя используют в работе два учебника: один выполняет развивающие функции, другой (традиционный) — нацелен на формирование вычислительных умений и навыков. Другие учителя увеличивают объем домашних заданий. Это приводит к перегрузкам школьников, провоцирует стрессовые ситуации, снижает интерес к математике [4, с. 5].
На основе результатов, полученных в ходе изучения и анализа учебников и программ по математике, нами была разработана совокупность заданий, направленных на улучшение качества формируемых знаний и увеличение количества усвоенных вычислительных приемов. Приведем примеры включения заданий по формированию вычислительных навыков в уроки математики.
На уроке по теме «Сложение трехзначных чисел с переходом через разряд» на этапе актуализации знаний учитель предлагает учащимся следующее задание: «Найдите значение выражений: 34 + 12; 84 + 15; 56 + 27; 67 + 32; 48–29; 23–14; 92–35; 75–38. Разделите данные выражения на две группы. По какому признаку вы разделили данные выражения?» [5, c. 54]. Работая с данным заданием, школьники будут выделять вычислительные приемы, на которых они основаны. При этом они повторяют приемы сложения и вычитания без перехода, с переходом через разряд и осознают правила, на которых они основаны.
Выполняя такие задания, учащиеся определяют, какие из них относятся к группе вычислений с переходом через разряд, а какие без перехода. Такие задания подготавливают школьников к более сложной работе (сложение трехзначных чисел с переходом через разряд).
На уроке по теме «Обратные операции» на этапе закрепления учитель предлагает учащимся следующее задание: «Найдите значение выражений: 42 + 30; 57 + 12; 67 + 19; 24 + 78. К каждому равенству напишите все возможные равенства с обратным действием. Какое это действие?» [6, c. 5]. При выполнении такого задания, у учеников закрепляется вычислительный навык сложения без перехода и с переходом через разряд. Так же формируется осознанность, так как при выполнении такого задания, детям нужно записать выражения с обратными действиями, что требует понимания взаимосвязи между компонентами и результатом действий сложения и вычитания.
На уроке по теме «Виды алгоритмов» на этапе изучения нового материала учитель включает следующие задания: «Пользуясь алгоритмом сложения двузначных чисел, вычисли суммы: 25 + 32 + 14; 16 + 28 + 50; 43 + 34 + 70; 81 + 39 + 87» [6, c. 33].
Выполняя подобное задание, учащиеся отрабатывают прием сложения двузначных чисел без перехода и с переходом через разряд. Действуя строго по алгоритму, младшие школьник легче усваивают выделенные приемы, так как ошибки в вычислениях приводят к ошибочному решению алгоритма, поэтому решение необходимо будет начать заново. А как известно, неоднократное повторение вычислительных действий приводит к его более прочному усвоению..
Во время урока по теме «Свойства сложения» при введении новой темы учитель просит учащихся найти в предложенных выражениях равные и вычислить их значение наиболее удобным способом.
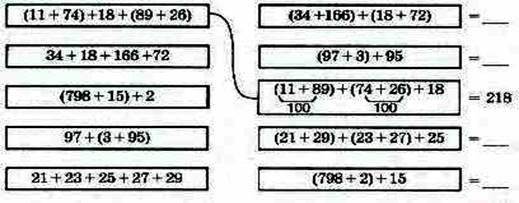
— Какие свойства сложения были использованы для упрощения вычислений? [6, c. 42].
При работе с подобным заданием перед школьниками стоит не только задача вычислить значение выражений, но и упростить процесс вычислений, используя свойства сложения, которые лежат в основе вычислительных приемов сложения без перехода и с переходом через разряд. Ученики повторяют и закрепляют эти приемы. В результате многократного использования данных приемов, они более прочно и осознано усваивают их.
На уроке по теме «Вычитание числа из суммы» на этапе закрепления учитель может предложить детям поиграть в «Лабиринт». Детям предлагается найти все возможные варианты «выхода» из лабиринта [6, c. 48].
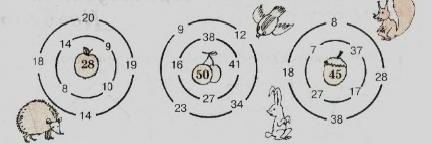
При работе с этим заданием от младших школьников требуется максимум внимания и осознанных вычислений, так как правильных вариантов заложено несколько. Школьника надлежит многократно пройти «лабиринты», находя то верные, то ложные пути, что обеспечит прочность закрепления приемов сложения и вычитания без перехода и с переходом через разряд.
Использование на уроках математики в начальной школе, на разных этапах их проведения подобных заданий, позволяет сформировать у младших школьников более прочные и осознанные вычислительные навыки. Многократное повторение одного и того же вычислительного приема обеспечивает наивысшее качество сформированных вычислительных приемов.
Обращая внимание на психофизиологические особенности ученика, нужно учитывать не только способ предложения материала для учащихся с аналитическим стилем мышления, но и для учащихся с синтетическим стилем.
Для учащихся с преобладанием синтетического типа мыслительной деятельности мы предлагаем использовать специальные схематические модели двузначных чисел, отражающих их десятичную структуру. На базе использования этих моделей строится адекватная схематическая модель приема вычисления, играющая роль внешней опоры, являющаяся образцом приема.
Курс математики начальной школы построен таким образом, в его основе лежит осознание разрядного состава двузначных и многозначных чисел и гораздо меньше внимания уделяется их десятичной структуре. Однако, десяток является основанием десятичной системы счисления. Это объясняется тем, что познакомить школьника с разрядным представление чисел можно уже в первом классе. При этом вводится понятие «разрядные слагаемые». При этом можно рассмотреть пример вида: 13 = 10 + 3, 48 = 40 + 8. Аналогично, для того чтобы показать школьникам десятичное разложение того же числа, пришлось бы использовать запись 48 = 10 × 4 + 8. А так как знакоместо с действием умножения по существующим программам обучения вводится во втором полугодии 2 класса, использование такого варианта объяснения недопустима на рассматриваемом этапе. Понятие разрядный состав двузначного числа мы рассматриваем для случаев так называемого «разрядного сложения и вычитания» в первом и втором классах, которые в дальнейшем становятся «опорными приемами» для обучения сложению и вычитанию с переходом через разрядную единицу.
В соответствии с изученным разрядным составом числа вводится схематическая модель, основанная на ранее изученных случаях.
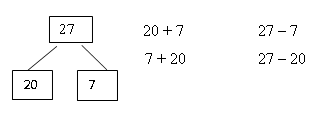
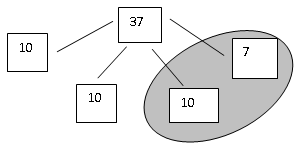
Использование модели в виде схемы двузначного числа на практических занятиях делает вычислительный прием более доступным непосредственному восприятию младшего школьника, позволяет избежать использования аналитической записи, отражающей десятичную структуру числа, которая на данном этапе обучения невозможна. Кроме того, предлагаемая модель повышает эффективность использования мыслительных особенностей учащихся данной возрастной категории. Данная методика введения вычислительного приема позволяет учитывать особенности мышления школьников с преобладанием синтетического типа мышления (а их среди учеников 1–2 классов 4–х летней начальной школы достаточно много), которые предрасположены к работе с наглядными моделями изучаемых понятий. Используемая модель двузначного числа позволяет ученику 2–3 класса в практической «ручной» деятельности смоделировать прием вычисления, а также является основой для самопроверки. Десятичная модель числа выглядит следующим образом (учащиеся назвали ее «солнышко»):
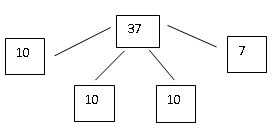
Этой моделью связаны следующие случаи сложения и вычитания:
37–7, 37–10, 37–20, 37 + 7
37–17, 37–27, 37–30, 7 + 30
Предложенная модель намного шире в использовании, нежели опора на разрядные модели. Кроме того, все рассмотренные варианты не выходят за рамки десятичного состава числа 37, отраженного в его схематической модели. Применяя эту модель, ученики могут не только усвоить рассмотренные случаи вычислений, четко осознав суть приема на наглядном уровне, но и оперируя руками (закрывая пальцем или ладонью вычитаемое), осуществляя тем самым проверку правильности полученного ответа: 37–17 = 20.
В процессе такой работы у учащихся формируется собственная траектория учебной деятельности. Так как у чисел второго десятка десятичная модель аналогична разрядной, то применение схематического приема моделирования, совместно с рассматриваемыми в учебнике предметными моделями (кубиками, палочками), будет пропедевтической:

Ежеурочное применение рассмотренных моделей для осознания десятичной структуры двузначного числа (2 класс) дает возможность создать прочную базу для усвоения вычислительных приемов в пределах 100, 1000.
Применяя эказанную модель, учитель может пользоваться специально составленными карточками-листами, в которых ученик работает как в тетради на печатной основе. Приведем пример серии заданий, в которых представлены подготовительный и основной этапы формирования вычислительного приема.
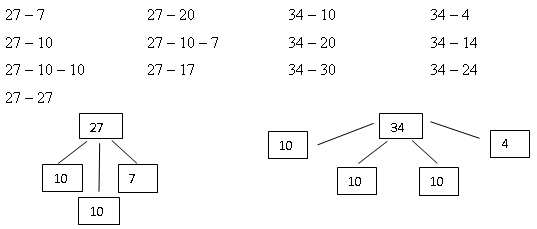
Рассматриваемая модель очень сильно облегчает арифметические вычисления младших школьников. Применяя эту модель, «слабые» ученики могут осваивать материал по индивидуальной траектории освоения и других случаев вычислений, например, 45 + 6.
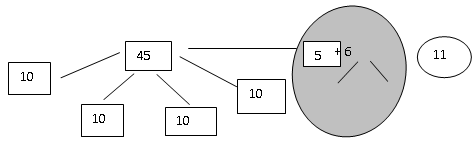
При этом в учебнике приводится следующая аналитическая запись:
45 + 6 = 45 + (5 + 1) = (45 + 5) + 1 = 50 + 1 = 51.
И следующая двушаговая запись:
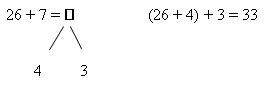
На первый взгляд кажется, что предлагаемая нами модель в виде схемы более громоздкая, неудобная, нежели в учебнике. Однако учащимся, о которых идет речь (синтетики, особенно с замедленным типом мышления, необходимо наличие наглядной внешней опоры для формирования осознанного способа деятельности), такая модель оказывается более эффективней своей наглядностью, а большая затрата труда и времени для построения этой модели (самостоятельного рисования десятичной системы числа) учащихся не пугает. Наоборот, позволяет подготовить учащихся к дальнейшей вычислительной деятельности. Применение моделей в виде схемы при рассмотрении нумерации в пределах 100 помогает быстро и качественно усвоить первые пять случаев сложения и вычитания в пределах 100. Дадим перечень этих случаев по учебнику «Математика», 2 класс:
30 + 20; 26 + 3; 60–20; 34–2; 34–20;
25 + 3; 26 + 304 50 + 234 26 + 4; 34–14.
Для остальных случаев также удобно использовать десятичную модель двузначного числа:
60–24; 45 + 23;
26 + 7; 57–26.
Например: 35–7
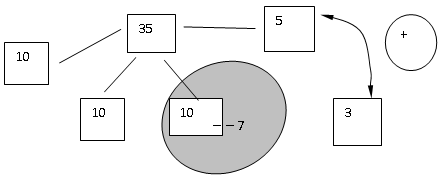
Опыт показал, что применение приема схематического моделирования числа при устных вычислениях в начальной школе является эффективным способом формирования собственной вычислительной траектории младшего школьника. После использования данной методики в течение полугода в большинстве случаев у младших школьников происходит интериоризация модели двузначного числа в виде схемы, то есть она переходит во внутренний план действий. Учащиеся становятся активными участника образовательного процесса.
Литература:
1. Трофименко, Ю. В. Проектирование и реализация педагогической технологии формирования профессиональных компетенций будущего учителя начальной школы // Диссертация на соискание ученой степени кандидата педагогических наук / Елецкий государственный университет им. И. А. Бунина. Елец, 2009.
2. Трофименко Ю. В. Формирование содержания профессиональной компетентности будущего учителя начальной школы в области изучения естественно-математических дисциплин//Аспирант и соискатель. 2009. № 5.
3. Трофименко, Ю. В., Пузина М. С. К вопросу о формировании устных вычислительных навыков младших школьников. В сборнике: Наука XXI века: теория, практика и перспективы. Сборник статей Международной научно-практической конференции. Ответственный редактор: Сукиасян Асатур Альбертович. Уфа, 2015.
4. Ильина О. Н. Проблема формирования вычислительных навыков младших школьников в современных условиях // Интернет журнал СахГУ «Наука, образование, общество». 2006. 3 февраля. URL статьи: http://journal.sakhgu.ru.
5. Петерсон Л. Г. Математика. 2 класс. Часть 1. М.: Издательство «Юнента», 2008.
6. Петерсон Л. Г. Математика. 2 класс. Часть 2. М.: Издательство «Юнента», 2008







