Методические особенности формирования первоначальных статистических представлений младших школьников

В статье рассмотрены методические аспекты формирования первоначальных статистических представлений младших школьников. Выявлены основные направления и особенности методики работы над заданиями с элементами математической статистики.

Ключевые слова: профессиональная компетентность, стохастика, элементы математической статистики.

 

В настоящее время становится необходима профессиональная подготовка учителей начальных классов к формированию у младших школьников первоначальных стохастических представлений. В модели профессионального развития основной акцент переносится на становление умения видеть, осознавать и оценивать различные проблемы, конструктивно разрешать их в соответствии со своими ценностными ориентациями, рассматривать любую трудность как стимул к дальнейшему развитию [1]. Система обучения стохастике направлена на познание окружающего мира средствами математики, общеинтеллектуальное, общекультурное развитие качеств мышления и качеств личности младшего школьника, необходимых для полноценного функционирования в современном обществе, для динамичной адаптации его к этому обществу, то есть на формирование у субъекта обучения в процессе изучения математики ключевых компетенций [2].

Изучение и анализ работы учителей по внедрению стохастической содержательно-методической линии в процесс обучения начальной школы позволяют сделать вывод, что основные причины трудностей кроются в недостатках их профессионально-педагогической подготовки [3, с.95].

Проблема нашей работы связана с выявлением теоретических и методических условий формирования профессиональной компетентности будущего учителя начальной − системы взаимосвязанных компонентов: фундаментальных предметных знаний, методических умений; профессионально-педагогических знаний и умений, профессионально значимых качеств личности учителя, которые реализуются в педагогической деятельности [4].

Эффективность подготовки учителей начальных классов в области формирования у младших школьников первоначальных стохастических представлений, будет достигнута, если подготовка построена на общих теоретических основаниях как система непрерывного образования, одной из целей которой является формирование профессиональной компетентности учителя начальных классов в указанной области [5]. Разработанная нами концептуальная модель формирования профессиональной компетентности студентов - будущих учителей начальной школы отражает характерные свойства, связи и отношения методической системы в доступной для анализа форме и обеспечивает переход теоретической сущности исследуемой проблемы в практическую действительность [6–8].

В содержании стохастической содержательно-методической линии выделяют три направления, методикой работы над которыми должен владеть будущий учитель: подготовка младших школьников в области комбинаторики, формирование первоначальных представлений о случайных событиях, формирование умений, связанных с представлением, сбором данных и их интерпретацией [1]. Статистическая составляющая заключается в сборе и анализе статистических данных, в ходе которых предусматривается ознакомление учащихся с простейшими способами регистрации и представления статистической информации, с возможностями ее использования для получения выводов об изучаемых явлениях и обеспечивает переход от реального мира к вероятностным моделям, связь их с реальной действительностью.

Целью изучения элементов математической статистики в начальной школе является формирование умений проводить несложные опросы, наблюдения с целью сбора количественной информации и ее оформления в виде таблиц, графиков, диаграмм; умений интерпретировать таблицы, схемы, графики, диаграммы.

К основным средствам формирования статистических представлений относят статистическое наблюдение и изображение получаемых сведений с помощью геометрических образов [8]. Статистическое наблюдение позволяет получить исходную информацию о некотором явлении или процессе. Графическое изображение полученных в результате наблюдений статистических сведений привлекает внимание, производит яркое и живое впечатление, становится более доходчивым и запоминающимся.

Одним из средств систематизации и обобщения полученных в наблюдениях статистических данных являются таблицы. Использование табличной формы позволяет расположить данные компактно, наглядно и рационально, за счёт чего облегчается их анализ, вскрываются те или иные характерные особенности изучаемых явлений: сходство и различие, взаимосвязь признаков и т. п.

При работе с таблицами в начальной школе следует отметить, что в самом простом случае таблица делится на строки и столбцы. Обычно каждый столбец имеет название, которое указывается в первой строке таблицы. Важно проиллюстрировать учащимся разнообразные таблицы и попросить привести примеры.

Задание 1. Узнай у друзей, какие конфеты им нравятся больше всего, и заполни такую же таблицу (каждый может назвать только один вид конфет). Расскажи, какие конфеты нравятся друзьям больше всего; меньше всего.

 

Цель рассмотрения подобных примеров — формирование у младших школьников представлений о том, что в жизни часто приходится сталкиваться с разнообразными таблицами, поэтому важно научиться пользоваться информацией помещенной в них и составлять их самим.

Задание 2. Рассмотрите таблицу и объясните, какой способ перебора всех вариантов в магазине расстановки сока предложен в этой таблице.

М - «Моя семья», И - «Иваныч», Д - «Добрый».

 

В процессе статистического наблюдения, если результаты записываются в том порядке, в котором они поступают, целесообразно составлять таблицу регистрации. Эта первичная таблица дает некоторое представление о связях, общих чертах и различиях получаемых статистических данных. В таблице исходных данных просматриваются не только объем совокупности, но и наиболее характерные ее черты: структура, типичные проявления, изменчивость признака и т. д. Представление о степени вариации однородных признаков дает простое сопоставление нескольких таблиц.

Задание 4. Используя таблицу, ответьте на вопросы. На сколько граммов печенье «Пуди» легче печенья «Орешки»? На сколько граммов печенье «Лазанки» тяжелее печенья «Колядки»? Чему равна масса печенья «Наполеоны»? Что легче печенье «Колядки» или печенье «Лазанки»?

 

В настоящее время появилась тенденция к расширению спектра использования различных методов решения задач. При сравнении данных, с увеличением числа объектов, целесообразно использовать графические изображения, позволяющие упросить рассуждения. Доступным для учащихся средством графического изображения статистических данных являются диаграммы, дающие обобщающую картину взаимосвязей единиц статистической совокупности и способствующие выявлению закономерностей.

Столбчатая диаграмма - это совокупность прямоугольников в одной полуплоскости с основаниями, принадлежащими одной прямой, и высотами, характеризующими различные единицы статистической совокупности. Она помогает закрепить представления о событиях «более возможных» и «менее возможных», сформировать представление о равновозможных событиях, даёт представление как о дискретных распределениях, так и о непрерывных. Использование столбчатых диаграмм позволяет делать выводы о степени разброса значений.

К рассмотрению диаграмм целесообразно перейти после того, как у младших школьников выработаны навыки работы с таблицами. Если с таблицами младшие школьники встречались ранее, то понятие диаграммы может оказаться для них совершенно новым. Поэтому начинать знакомство учащихся с диаграммами разумнее с конкретного примера, иллюстрирующего, что такое диаграмма и для чего она нужна. Для этого можно рассмотреть, например, такую задачу.

Задание 5. Дайте ответы на вопросы, используя диаграмму (Рис. 1). Сколько литров молока: а) в большом и маленьком пакете? б) в среднем и маленьком? в) в трех пакетах? На сколько литров молока больше в большом пакете, чем в маленьком?

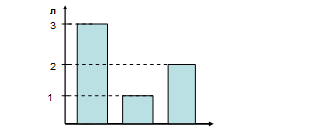
Рис. 1.

 

Пользуясь рисунком, учащиеся быстро и правильно ответят на поставленные вопросы. Наибольшие затруднения учащихся вызывает построение диаграмм, поэтому учителем должен быть четко сформулирован алгоритм построения столбчатых диаграмм.

Задание 6. Мебельная фабрика приняла заказ на изготовление партии из 3000 стульев. Каждый из стульев по плану должен весить 900 грамм. Но контрольное взвешивание изготовленной партии стульев дало следующие результаты (результаты взвешивания представлены в виде таблицы):

 

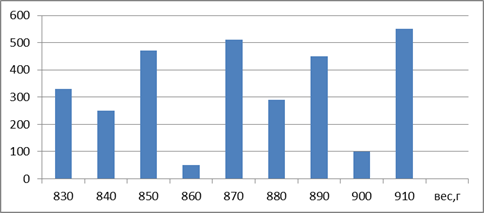
Рис. 2.

 

Ответьте на вопросы: «Стульев какого веса завод выпустил больше всего? Сколько стульев весом 850 грамм выпустил завод? Стульев какого веса завод выпустил меньше всего? Сколько стульев весом меньше 900 грамма произвел завод?».

Важно выработать у учащихся четкий алгоритм построения столбчатых (линейных) диаграмм: подобрать цену деления шкалы, удобную для обозначения на ней значений данных величин; изобразить шкалу на вертикальном координатном луче, а на горизонтальном луче отметить на равном расстоянии друг от друга точки по числу имеющихся величин; от выбранных точек построить вертикальные отрезки (столбцы), высота которых равна значению соответствующей величины.

Диаграмму, построенную таким способом, называют столбчатой диаграммой, но если вместо столбиков изобразить линии той же высоты, получим новый вид диаграммы — линейную диаграмму. Далее целесообразно предложить учащимся построить несколько диаграмм для отработки шагов алгоритма с разбором у доски.

Статистическую информацию можно изображать с помощью круговой (секторной) диаграммы, которая представляет собой круг, разделенный на секторы с площадями, пропорциональными частотам. Круговые диаграммы показывают, прежде всего, состав статистической совокупности, ее структуру и располагают большими возможностями для ознакомления учащихся с начальными идеями так называемого метода Монте-Карло получения экспериментальных значений случайной величины.

Задание 6. После окончания четверти учитель представил результаты оценок по математике с помощью диаграммы. По данным диаграммы (Рис.3) ответь на вопросы. Сколько учеников получили оценку «пятерка»? Сколько учеников получили оценку «четверка»? Сколько учеников получили оценку «тройка»? Сравни количество учеников, получивших оценку «пятерка» и количество учеников, получивших остальные оценки.

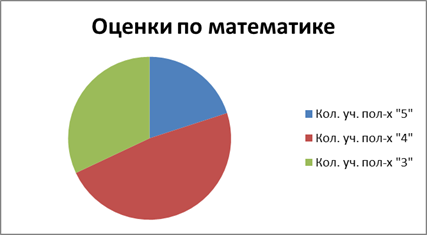
Рис. 3.

 

Цель задания: научить младших школьников «читать» информацию, представленную в диаграмме, сравнивать между собой различные данные и делать определенные выводы.

Такая диаграмма представляет круг, разрезанный на дольки, каждая из долек соответствует одному из значений изучаемого признака (в нашем случае — пол ребенка), ее размер пропорционален интересующей нас величине (количеству новорожденных данного пола). При изучении данной темы у учащихся должен быть сформирован четкий алгоритм построения круговых диаграмм: найти часть целого, которая приходится на каждую из величин; найти величины центральных углов, соответствующих каждой части; построить в данной окружности центральные углы, соответствующие каждой части.

Целесообразно предложить учащимся выполнить задания на построение круговых диаграмм по таблицам данных. Важно обратить внимание младших школьников на возможность взаимозаменяемости различных видов диаграмм. На вопрос учителя «Можно ли, глядя на столбчатую диаграмму, построить по ней линейную?» учащиеся без труда должны ответить «да», поскольку надо всего заменить столбики линиями соответствующей высоты. Значит, используя столбчатую диаграмму, можно построить линейную, и наоборот. Аналогично, из столбчатой или линейной диаграммы можно построить круговую, и наоборот. Для закрепления навыков нужно предложить школьникам задания, требующие построить диаграмму другого вида по имеющейся.

Ценность заданий стохастического характера определяется не только тем аппаратом, который используется при их решении, но и возможностями продемонстрировать процесс применения математики для решения практических проблем. Стохастические задачи, знакомящие младших школьников со сферой случайных событий и формирующие у них первоначальные статистические представления, способствуют познанию окружающего мира средствами математики. Статистическая составляющая дает возможность сравнивать совокупности данных по степени их вариации, помогая пониманию изменчивости, скрывающейся за средними показателями. Количественная оценка степени вариации потребуется выпускнику школы для простейшего сравнения производственных показателей, правильному осмыслению происходящих в окружающей жизни событий.

Анализ статистических данных постепенно убеждает учащихся, что собранный материал рассматривается не ради него самого, а лишь как некоторая пробная группа, представляющая только один из возможных вариантов исследования. На основании результатов наблюдений или измерений они учатся делать выводы относительно более широкого круга явлений. Так они начинают познавать основные идеи и понятия выборочного метода и учатся в простейших случаях пользоваться им на практике.

 

Литература:

 

1.                  Проценко Е. А., Трофименко Ю. В., Семенова Г. А. Методические аспекты обучения младших школьников элементам математической статистики. Молодой ученый. 2014. № 11. С. 404–408.

2.                  Проценко Е. А., Трофименко Ю. В. Методические аспекты обучения младших школьников стохастике. Молодой ученый. 2013. № 11. С. 633–637.

3.             Проценко Е. А., Трофименко Ю. В. Формирование профессиональной компетентности будущих учителей начальной школы при обучении стохастике. Вестник Таганрогского государственного педагогического института. 2013. № 1. С. 094–100.

4.                  Проценко, Е. А. Концептуальная модель формирования профессиональной компетентности будущих учителей начальной школы при обучении стохастике//Вопросы гуманитарных наук. -2008. -№ 3 (36). -С. 285–292.

5.                  Проценко, Е. А. Теоретические и методические основы изучения комбинаторики в начальной школе / Е. А. Проценко, Г. А. Семенова. -Таганрог: Изд-во Таганрог. гос. пед. ин-та, 2008. -128 с.

6.                  Проценко, Е. А. Использование информационных технологий как средства организации самостоятельной работы студентов//Известия высших учебных заведений. Северо-Кавказский регион. Серия: Естественные науки. -2006. -№ S16. -С. 77–81.

7.                  Проценко, Е. А. Применение компьютерных средств обучения в процессе преподавания комбинаторики//Вестник Московского городского педагогического университета. -2006. -№ 6. -С. 167–170.

8.                  Проценко Е. А., Трофименко Ю. В. Методические аспекты обучения младших школьников комбинаторике. Молодой ученый. 2014. № 67. С. 633–637.