Поставлена математическая задача о коррупции на основе модели системы «властных иерархий», разработанной Михайловым А. П. Математическая модель представляет собой краевую задачу для нелинейного дифференциального уравнения в частных производных.
Ключевые слова: краевые задачи, математическое моделирование, коррупция.
Производственная деятельность человека сопровождается созданием им материальных ценностей, промышленных объектов, перераспределением ресурсов, как между различными слоями социального общества, так и между различными географическими регионами. Распределение ресурсов не может быть «справедливым» ни для целей организации создания новых ценностей, ни для удовлетворения личных потребностей и запросов отдельных групп лиц, участников социальной и экономической деятельности. В отдельных «точках» производственных и межличностных взаимоотношений человека возникают механизмы решения поставленных задач не оговоренные моральными и договорными соглашениями такие, как злоупотребление служебным положением, дача или получение взятки, незаконное использование физическим лицом или группой лиц своего должностного положения вопреки законным интересам общества и государства. Часть нарушений такого рода в рамках законодательств различных стран относится к коррупции [8, 13, 24, 34, 39, 59, 64, 72, 95].
Коррупция может пронизывать все уровни системы управления — от низовых структур до вершин государственной власти. В большинстве стран она охватывает политиков и чиновников всех уровней, принимающих политические и экономические решения. Как разлагающий общественную безопасность этот феномен имеет способность поражать, не смотря на борьбу с ней [1, 12, 15, 35, 66, 68], не только государственные структуры управления, но и негосударственные, общественные или коммерческие организации: здравоохранение [6], экономику [2, 41, 79, 83], систему государственных закупок [20], природопользование [62], вооруженные силы [63, 75], систему образования [85], бизнес сообщество [11].
Коррупционеры используют свое положение в системе социально-экономических взаимоотношений не только для решения задач в интересах общества, но и в личных целях методами, не предусмотренными установленными правилами. В некоторых случаях использование служебных полномочий в личных целях сопровождается и ускоренным решением частных общественных задач [10, 41]. Однако, в целом, коррупция оказывает отрицательное воздействие на системы управления и социальные взаимоотношения в обществе [44, 74, 76, 89, 91, 92, 94]. Это явление уходит корнями в далекое прошлое и отсутствие противодействия ей приводит к ее разрастанию и проникновению во все сферы жизни человека и со временем может представлять угрозу безопасности государства [14, 31, 42, 65, 67, 74].
Территория России разделена на 8 территориальных округов — Центральный, Северо-Западный, Южный, Приволжский, Уральский, Сибирский, Дальневосточный, Северо-Кавказский [81], расположенных на разных расстояниях от центрального округа. Каждый округ имеет свою промышленность, сельское хозяйство, административный аппарат, бюджет, доходы, финансовые долги, производимую продукцию и т. п. Регионы расположены в различных климатических поясах с различными природными ресурсами. Существенно отличаются их производственные мощности и номенклатура выпускаемой продукции. Поэтому оценить эффективность управления регионом, исходя из каких-либо экономических показателей, не представляется возможным. Соответственно трудно оценить и размер коррупции в стране, исходя из статистических данных по РФ [45, 82].
Большинство работ, посвященных исследованию коррупции, основывается не на криминальной статистике, а на социологических исследованиях [19, 44]. Поэтому значительное число разработанных моделей, прежде всего математических, трудно сопоставить с реальными статистически данными. Тем не мене на основе анализа результатов решения математических задач можно оценить ущерб от коррупционной деятельности и предложить варианты управленческих решений по ограничению коррупции. При разработке математических моделей коррупции широко используется аппарат математической теории игр [16, 26, 28, 29, 33, 37, 46], методы и формализм теории потоков в сетях [18, 32, 36, 43, 77] с учетом наличия систем управления [61, 93]. Разрабатываются статистические модели коррупции [27, 86], модели борьбы с ней [3, 25, 38, 69, 90] и модели социального контроля [4, 87, 88]. Предлагаются различные модели межличностных взаимоотношений [17, 50, 80, 84] и модели формирования групп [9, 56, 60, 73]. Ниже предлагается математическая модель коррупции, за основу которой взята модель Михайлова А. П. «власть общество» [70, 71]. В модели используется аппарат уравнений в частных производных, а сама модель основывается на концепциях механики сплошных сред с учетом протекающих в них реакций [48, 70, 78, 97, 98].
Модель коррупции. В модели «власть-общество» [70, 71] за основу берется совокупность властных полномочий в системе «властных иерархий». В модель вводится функция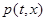 
, описывающая плотность распределение властных полномочий на одного представителя власти на территории. В количественном отношении это может быть, например, общий объем ресурсов, которые распределяет властная структура на текущий момент времени. Предполагается, что властные полномочия передаются от точки к точке по принципу близкодействия. Этот процесс в модели можно описать на основе принципов, используемых для описания систем «реакция-диффузия». В реально существующей системе «центр-периферия» властные полномочия убывают от центра к периферии. Поэтому функция 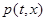должна быть убывающей функцией координаты, если считать, что центр расположен в начале координат. Поскольку властные полномочия на местах передаются обществу, то в модель вводится «реакция общества» в виде функции 
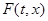. Динамика распределения власти, в разработанной в [70, 71] модели, для отрезка 
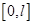описывается уравнением
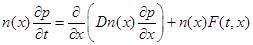, (1)
где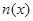 
— плотность распределения числа представителей властной структуры на территории, 
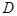— положительная постоянная. К этому уравнению добавляются граничные условия
,
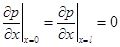соответствующие «наполнению» властных полномочий на концах отрезка, и начальные условия
.
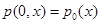Общее количество полномочий на всей территории подсчитывается по формуле
,
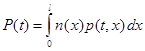а общее количество представителей властных структур —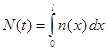 
.
В «базовой» модели [70, 71] предлагается принять экспоненциальное распределение чиновников вдоль отрезка (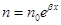
,
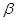— постоянная) растущее от центра к периферии, и принимается, что
,
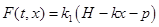где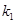 
, 
, 
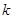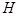— положительные постоянные. Таким образом, уравнение (1) при этих предположениях принимает вид
.
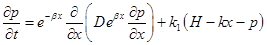Это уравнение приводится к виду
.
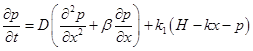Если слагаемое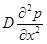 
в этом уравнении описывает «естественную» передачу полномочий [70], то слагаемое 
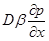сопоставляется с конвективным переносом полномочий со скоростью 
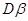. При положительных значениях параметра 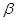(численность аппарата увеличивается от центра к периферии) часть полномочий будет возвращаться центру, а при отрицательных 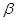— передаваться от центра к периферии.
Под коррупцией в рассматриваемой модели можно понимать утрату части полномочий властными структурами на территории:
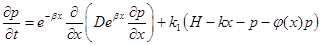. (2)
В этом уравнении функция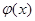 
— плотность распределения потерь, вызванных коррупцией, властных полномочий, теряемых системой власть-общество при решении общественных задач. Общие коррупционные потери 
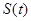на отрезке естественно считать пропорциональными утрате части полномочий
,
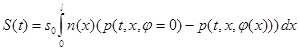где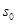 
— положительная постоянная.
В дальнейшем принимается, что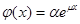 
, где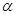 
— положительная постоянная, а постоянная 
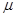считается отрицательной, если потеря властных полномочий уменьшается от центра к периферии, и положительной в противном случае.
Численные эксперименты. Численность работников органов государственной власти и местного самоуправления в РФ изменяется от 9 на 1000 жителей в Центральном округе и до 15 в Дальневосточном округе [81]. Если принять за единицу длины расстояние между этими округами, то постоянную 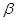в (2) следует принять равной 0.5, а 
, 
, 
, 
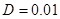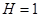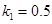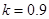[70, 71]. Численное решение уравнения (2) осуществлялось с применением метода сеток [55].
Распределение полномочий в моменты времен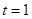и 
и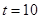 
представлены на рис. 1. Динамика изменения общих коррупционных потерь во времени пр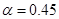и 
и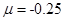 
, 
, 
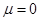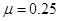приведена на рис. 2. Как следует из полученных результатов для модели (2) распределение «властных» полномочий убывает от центра к периферии (рис. 1). «Коррупционные» потери при возрастающей численности чиновников от центра к периферии (
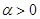в (2)) будут меньше в том случае, если число коррупционеров будет убывать по мере удаления от центра (при 
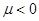), и будут больше, если число «коррупционеров» будет возрастать от центра к периферии. Зависимости 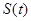, приведенные на рис. 2, согласуются со статистическими данными по числу осужденных за коррупционные преступления в США 1970 по 2006 год (рис. 3, [19]). На рис. 3 символом * отмечены статистические данные, а сплошная линия соответствует «логистической» зависимости с удельной скоростью роста равной 0.3.
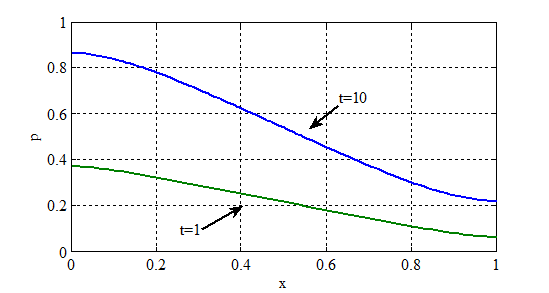
Рис. 1.
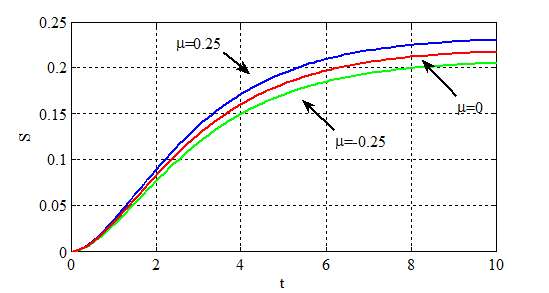
Рис. 2.
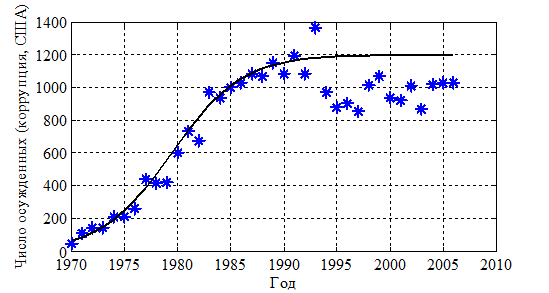
Рис. 3.
Динамика изменения числа осужденных в США за коррупционные преступления близка к «логистической» зависимости. Аналогичной зависимостью описываются и экспериментальные данные по кинетике роста растений [47, 57, 58]. Аналогичные расчетные зависимости следуют из некоторых моделей для живых систем [54, 60]. Поэтому для описания коррупционных явлений можно использовать и методы построения моделей в задачах популяционной биологии и социальной самоорганизации, основывающиеся на различных типах взаимоотношениях между биологическими сообществами и социальными группами [7, 17, 46, 50, 60]. Коррупционная система может быть представлена и как неизлечимое заболевание или как орган живой функциональной системы, работающий только при поступлении в него питательных веществ [5, 21, 40, 49, 96, 99]. Она может рассматриваться и как биологическое сообщество, являющееся, например, хищником по отношению к социальному сообществу [22, 23, 51–54]. Последнее можно рассматривать как сообщество, находящееся под влиянием внешних «агрессивных» сред [30, 47].
Заключение. Разработанная модель «коррупции», в основе которой лежит модель «власть-общество» А. П. Михайлова, не учитывает наличие материальных ресурсов, необходимых для существования, как самой системы, так и коррупционного сообщества внутри него. Наряду с экономической составляющей не учитываются и противодействующие коррупции социальные и политические движения в обществе. Тем не менее, она отражает реальное распределение властных полномочий в системе «центр-периферия» и возможный варианты «коррупционных» потерь.
Литература:
1. Айрапетян Э. С. Механизм эффективного противодействия коррупции, его элементы и совершенствование // Молодой ученый. — 2013. — № 3. — С. 342–344.
2. Алферова А. Б. Коррупция как фактор изменения политической лояльности // Молодой ученый. — 2011. — № 11–2. — С. 46–48.
3. Антоненко А. В., Угольницкий Г. А., Усов А. Б. Статические модели борьбы с коррупцией в иерархических системах управления // Известия Российской академии наук. Теория и системы управления. — 2013. — № 4. — С. 164.
4. Ардельянова Я. А. Модели социального контроля коррупции и возможности их реализации в России // Пространство и Время. — 2013. — № 1 (11). — С. 182–187.
5. Балыкина Ю. Е., Колпак Е. П. Математические модели функционирования фолликула щитовидной железы // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2013. — № 3. — С. 20–31.
6. Барановская Е. А., Аксенова-Сорохтей Ю. Н. К вопросу о коррупциогенных рисках в системе здравоохранения //Приволжский научный вестник. — 2015. — № 3–2 (43). — С. 21–23.
7. Басков О. В. Критерий непротиворечивости «квантов» информации о нечетком отношении предпочтения лица, принимающего решения // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2014. — № 2. — С. 12–18.
8. Басова Л. А. Является ли коррупция нормой? (нормативно-правовые основания коррупционного поведения, на примере Г. Ярославля) // Молодой ученый. — 2011. — № 11–2. — С. 6–8.
9. Белогривцева М. В., Гвоздарёва Л. П. Модель принятия решений об участии в коррупции и ее применение // Вестник Астраханского государственного технического университета. Серия: Экономика. — 2011. — № 1. — С. 29–35.
10. Бидова Б. Б. Для кого — взятка, для кого — оплата услуг? // Молодой ученый. — 2014. — № 18. — С. 683–685.
11. Боккоева Г. Н. Противодействие коррупции и теневой экономике в целях улучшения делового климата бизнес-сообщества // Молодой ученый. — 2013. — № 12 (59). — С. 252–255.
12. Бородина А. Ю. Универсальная электронная карта как инструмент в борьбе с коррупцией // Молодой ученый. — 2014. — № 1. — С. 205–208.
13. Бочарова А. Э. Коррупция в России // Молодой ученый. — 2014. — № 21 (80). — С. 499–501.
14. Бугров К. Д. Коррупция и разложение Российской Империи: античные модели критической мысли в российской политической культуре второй половины XVIII в. // Уральский исторический вестник. — 2011. — № 3 (32). — С. 105–113.
15. Бузун Е. В. Роль правовой культуры в преодолении коррупционных факторов в правотворчестве // Молодой ученый. — 2013. — № 7. — С. 269–271.
16. Буре А. В. Об одной теоретико-игровой модели тендера // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2015. — № 1. — С. 25–32.
17. Буре В. М., Екимов А. В., Свиркин М. В. Имитационная модель формирования профиля мнений внутри коллектива // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2014. — № 3. — С. 93–98.
18. Валиотти Н. А. Нейросетевая модель для дифференцированной оценки влияния одновременных внешних событий в сфере розничной торговли // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2014. — № 2. — С. 93–98.
19. Верховин В. И. Насколько эффективна западная система инфорсмента? // Личность. Культура. Общество. — 2011. — Т. XIII. — № 4 (67–68). — С. 141–150.
20. Вершинина Е. С. Коррупционная составляющая государственных закупок // Молодой ученый. — 2015. — № 3 (83). — С. 626–630.
21. Гасратова Н. А., Бойцов Д. С., Габриелян Л. А., Тюганова Т. М. Математическая модель иммунного ответа организма млекопитающих на поражение кожи ожогом // Молодой ученый. — 2014. — № 12 (71). — С. 1–7.
22. Гасратова Н. А., Столбовая М. В., Бойцов Д. С., Степанова Д. С. Математическая модель хищник-жертва на линейном ареале // Молодой ученый. — 2014. — № 11. — С. 1–10.
23. Гасратова Н. А., Столбовая М. В., Неверова Е. Г., Бербер А. С. Математическая модель «ресурс-потребитель» // Молодой ученый. — 2014. — № 10 (69). — С. 5–14.
24. Головченко А. В. Криминологическая характеристика коррупции // Молодой ученый. — 2009. — № 11. — С. 207–210.
25. Горбанева О. И. Статические модели учета фактора коррупции при распределении ресурсов в иерархических системах управления // Известия Южного федерального университета. Технические науки. — 2012. — № 6 (131). — С. 207–211.
26. Горбанева О. И., Угольницкий Г. А Теоретико-игровые модели распределения ресурсов при управлении качеством речной воды в условиях коррупции. Часть II // Эвристические алгоритмы и распределенные вычисления. — 2014. — Т. 1. — № 2. — С. 21–29.
27. Горбанева О. И., Угольницкий Г. А. Статистические модели учета фактора коррупции при распределении ресурсов в трехуровневых системах управления // Управление большими системами: сборник трудов. — 2013. — № 42. — С. 195–216.
28. Горбанева О. И., Угольницкий Г. А. Теоретико-игровые модели распределения ресурсов при управлении качеством речной воды в условиях коррупции. Часть I // Эвристические алгоритмы и распределенные вычисления. — 2014. — Т. 1. — № 1. — С. 16–24.
29. Горбанева О. И., Усов А. Б., Угольницкий Г. А. Модели коррупции в иерархических системах управления // Проблемы управления. — 2015. — № 1. — С. 2–10.
30. Горбунова М. В., Колпак Е. П., Крицкая А. В. Математическая модель антропогенного воздействия на одиночную популяцию. В сборнике: Синергетика в общественных и естественных науках: девятые Курдюмовские чтения материалы Международной междисциплинарной научной конференции с элементами научной школы для молодежи. редкол.: Лапина Г. П. (отв. ред.) и др.. Тверь, 2013. С. 165.
31. Грачев С. И., Морозова А. С. Коррупция как фактор существования терроризма // Вестник Казанского юридического института МВД России. — 2015. — № 1 (19). — С. 68–71.
32. Денин К. И. Математическая модель множественной коррупции в системе управления приемлемым развитием // Известия высших учебных заведений. Северо-Кавказский регион. Серия: Естественные науки. — 2007. — № 3. — С. 3–5.
33. Денин К. И., Угольницкий Г. А. Теоретико-игровая модель коррупции в системах иерархического управления // Известия Российской академии наук. Теория и системы управления. — 2010. — № 1. — С. 156–162.
34. Дзотов Ч. А. Институт юридической клиники как средство противодействия коррупции // Молодой ученый. — 2012. — № 5. — С. 326–328.
35. Добрынин Л. А. Российская модель системной коррупции и стратегия ее преодоления // Экономика и управление. — 2012. — № 6 (80). — С. 30–35.
36. Домашук П. В. Информационное моделирование коррупции // Образовательные ресурсы и технологии. — 2015. — № 1 (9). — С. 119–125.
37. Епархина О. В. Моделирование коррупции // Ярославский педагогический вестник. — 2013. — Т. 1. — № 1. — С. 110–116.
38. Епархина О. В. Моделирование коррупции: параметры, условия, возможности // Вестник Ярославского государственного университета им. П. Г. Демидова. Серия Гуманитарные науки. — 2011. — № 3. — С. 124–125.
39. Жадан В. Н. О коррупции и криминологической характеристике коррупционных преступлений // Молодой ученый. — 2015. — № 5 (85). — С. 345–351.
40. Жукова И. В., Колпак Е. П. Математические модели злокачественной опухоли // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2014. — № 3. — С. 5–18.
41. Заикин Н. Н. Роль конкуренции и коррупции в модели экономического роста // Вестник Астраханского государственного технического университета. Серия: Экономика. — 2014. — № 1. — С. 14–21.
42. Зайончковский П. А. Правительственный аппарат самодержавной России в XIX в. М.: Мысль, 1978. — 288 с.
43. Зенюк Д. А., Малинецкий Г. Г., Фаллер Д. С. Имитационная модель коррупции в иерархических системах // Компьютерные исследования и моделирование. — 2014. — Т. 6. — № 2. — С. 321–329.
44. Исагалиева А. С., Зулькорнеева Л. И. Уровень доверия граждан города Астрахани к государственной власти (на примере конкретного социологического исследования) // Молодой ученый. — 2014. — № 2 (61). — С. 677–680.
45. Карманов М. В. Статистика и коррупция в современной России // Вопросы статистики. — 2013. — № 2. — С. 83–86.
46. Колабутин Н. В. Двухуровневая кооперация в дифференциальной игре технологического альянса // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2015. — № 1. — С. 42–63.
47. Колесин И. Д., Старков В. Н., Гасратова Н. А. Одиночная популяция под антропогенным давлением // Журнал научных публикаций аспирантов и докторантов. — 2014. — № 6 (96). — С. 226–232.
48. Колпак Е. П. Введение в механику сплошных сред учебное пособие / Е. П. Колпак; С.-Петерб. гос. ун-т. СПб. 2004.
49. Колпак Е. П., Балыкина Ю. Е., Котина Е. Д., Жукова И. В. Математическая модель нарушений функционирования щитовидной железы // Молодой ученый. — 2014. — № 2 (61). — С. 19–24.
50. Колпак Е. П., Бронникова А. И., Полежаев В. Ю. Математическая модель стачечного движения в России в начале XX века // Молодой учёный. — 2015. — № 3 (83). — С. 4–15.
51. Колпак Е. П., Габриелян Л. А., Бронникова А. И., Крылова В. А. О математических моделях симбиоза // Молодой ученый. — 2015. — № 4 (84). — С. 6–14.
52. Колпак Е. П., Горбунова Е. А., Балыкина Ю. Е., Гасратова Н. А. Математическая модель одиночной популяции на билокальном ареале // Молодой ученый. — 2014. — № 1. — С. 28–33.
53. Колпак Е. П., Горбунова Е. А., Столбовая М. В., Балыкина Ю. Е. Математическая модель логистической популяции на линейном ареале // Молодой ученый. — 2014. — № 3 (62). — С. 6–14.
54. Колпак Е. П., Горыня Е. В., Крылова В. А., Полежаев Д. Ю. Математическая модель конкуренции двух популяций на линейном ареале // Молодой ученый. — 2014. — № 12 (71). — С. 12–22.
55. Колпак Е. П., Жукова И. В., Степанова Д. С., Крицкая А. В. О. численных методах решения эволюционных уравнений на примере математической модели «хищник-жертва» // Молодой ученый. — 2014. — № 4. — С. 20–30.
56. Колпак Е. П., Скороходова Т. В. Математическая модель роста числа учащихся в средней и высшей школах России. В сборнике: Синергетика в естественных науках. Восьмые Курдюмовские чтения материалы Международной междисциплинарной научной конференции с элементами научной школы для молодежи. Ответственный редактор: Лапина Г. П.. Тверь, 2012. С. 274–275.
57. Колпак Е. П., Столбовая М. В. Математическая модель кинетики роста растений // Журнал научных публикаций аспирантов и докторантов. — 2013. — № 12 (90). — С. 230–232.
58. Колпак Е. П., Столбовая М. В. Математическая модель роста растений. В сборнике: Синергетика в общественных и естественных науках: девятые Курдюмовские чтения материалы Международной междисциплинарной научной конференции с элементами научной школы для молодежи. редкол.: Лапина Г. П. (отв. ред.) и др.. Тверь, 2013. С. 186
59. Коновалова О. М. Криминологическая характеристика коррупции // Молодой ученый. — 2014. — № 1. — С. 231–233.
60. Крылова В. А., Колпак Е. П., Сыромолотова К. И., Воротова Т. А. Математические модели формирования спортивных групп // Молодой учёный. — 2015. — № 8 (88). — C. 10–19.
61. Кузин В. И. Модель влияния коррупции на региональное развитие // Стратегия устойчивого развития регионов России. — 2013. — № 16. — С. 25–30.
62. Кузнецов А. В. К вопросу о коррупционных преступлениях в области охраны природных ресурсов (криминологический аспект) // Вестник Омской юридической академии. — 2015. — № 1 (26). — С. 73–77.
63. Кулагина В. Н. Основные принципы противодействия коррупции в вооруженных силах Российской Федерации // Международный научно-исследовательский журнал. — 2014. — № 3–2 (22). — С. 99.
64. Кусакина Е. А., Устинов А. А. Социально-психологические факторы, влияющие на коррупционные правонарушения в уголовно-исполнительной системе // Молодой ученый. — 2013. — № 1. — С. 265–266.
65. Лаптев Р. А., Коварда В. В., Шатунова А. Р. Понятие и виды коррупции как социального и исторического явления // Молодой ученый. — 2014. — № 18. — С. 386–388.
66. Латов Ю. В. Коррупция в системе угроз национальной безопасности России // Актуальные проблемы экономики и права. — 2015. — № 1 (33). — С. 46–53.
67. Ломакин С. В. Налоги и коррупция как элементы развития оппортунизма в РФ // Молодой ученый. — 2013. — № 11. — С. 380–383.
68. Магомадов Н. С. Х. Коррупция в современном российском обществе: состояние и борьба с ней // Молодой ученый. — 2015. — № 6 (86). — С. 497–499.
69. Матвеев А. В. Основные модели противодействия коррупции // Фундаментальные и прикладные исследования в современном мире. — 2013. — Т. 2. — № 4 (04). — С. 42–45.
70. Михайлов А. П. Моделирование системы «власть-общество». М.: ФИЗМАТЛИТ, 2006. — 144 с.
71. Михайлов А. П., Ланкин Д. Ф. Моделирование оптимальных стратегий ограничения коррупции // Математическое моделирование. — 2006. — Т. 18. — № 12. — С. 115–124.
72. Михалева Г. В., Ромашова Т. В. Некоторые вопросы правового обеспечения борьбы с коррупцией // Молодой ученый. — 2014. — № 2 (61). — С. 588–592.
73. Морозова Н. С. Виртуальные формации и виртуальные лидеры в задаче о движении строем группы роботов // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2015. — № 1. — С. 135–149.
74. Нагимова А. М. Коррупция как фактор торможения процессов реформирования общества // Научные труды Центра перспективных экономических исследований. — 2013. — № 6. — С. 189–194.
75. Окунева К. Д. Совершенствование порядка безвозмездной передачи военного имущества в муниципальную собственность как направление по повышению эффективности противодействия коррупции // Право в Вооруженных силах. — 2015. — № 1 (211). — С. 11–14.
76. Патокина Е. А. Цикличная бюрократия и коррупция: человеческий фактор как связующее звено между «идеальной» и «неидеальной» бюрократией // Молодой ученый. — 2011. — № 11–2. — С. 92–94.
77. Полякова Л. Н., Карелин В. В., Буре В. М., Хитров Г. М. Точные штрафные функции в задаче управления одной системой массового обслуживания // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2015. — № 1. — С. 75–82.
78. Пронина Ю. Г. Оценка устойчивости упругой трубы под давлением коррозионных сред Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2006. — № 3. — С. 55–63.
79. Прохорова И. А. Коррупция и теневая экономика в деятельности ФНС. Послание президента // Молодой ученый. — 2014. — № 21 (80). — С. 409–412.
80. Розин М. Д., Сущий С. Я., Угольницкий Г. А., Антоненко А. В. Дескриптивный подход к моделированию коррупции как фактора социальной конфликтности // Инженерный вестник Дона. — 2011. — Т. 17. — № 3. — С. 412–423.
81. Российский статистический ежегодник. М.: Статистика России, 2013. — 717 с.
82. Рузанов Д. П. Коррупция: теоретические модели и эмпирические исследования // Научные труды Вольного экономического общества России. — 2010. — Т. 133. — С. 262–271.
83. Румянцева Е. Е., Тер-Овсепян С. В. Методология количественной оценки совокупного финансово-экономического ущерба от коррупции // Научный журнал НИУ ИТМО. Серия: Экономика и экологический менеджмент. — 2015. — № 1. — С. 213–219.
84. Рыжкин А. И., Усов А. Б Математическая модель борьбы с коррупцией в системе контроля водяного балласта судов // Известия высших учебных заведений. Северо-Кавказский регион. Серия: Естественные науки. — 2013. — № 4 (176). — С. 17–20.
85. Ряузова Е. П. Коррупция в школе: причины, методика расследования и методы противодействия // Законность и правопорядок в современном обществе. — 2015. — № 23. — С. 83–85.
86. Северцев Н. А., Фесечко А. И. Логико-вероятностные модели риска взяток и коррупции // Труды международного симпозиума Надежность и качество. — 2010. — Т. 2. — С. 208–211.
87. Семенчин Е. А., Новикова О. С., Новиков С. Ю. Приватизация в условиях коррупции и ее моделирование // Наука. Инновации. Технологии. — 2006. — № 1. — С. 85–87.
88. Смагин В. Н. Модель взятки и оценка потерь от коррупции // Вестник Южно-Уральского государственного университета. Серия: Экономика и менеджмент. — 2015. — Т. 9. — № 1. — С. 39–45.
89. Терехова Т. А. Влияние личностных особенностей на склонность к коррупционной деятельности // Молодой ученый. — 2011. — № 11–2. — С. 122–127.
90. Угольницкий Г. А., Усов А. Б. Моделирование коррупции в трехуровневых системах управления // Проблемы управления. — 2014. — № 1. — С. 53–62.
91. Хаванова И. С. Высокий уровень психологической устойчивости личности как значимый фактор противодействия коррупции // Молодой ученый. — 2014. — № 15. — С. 242–244.
92. Чернов Е. Н. Коррупция и ее отрицательное воздействие на развитие карьеры государственных служащих // Молодой ученый. — 2013. — № 12 (59). — С. 798–801.
93. Чернушкин А. А. Модель оптимальной эксплуатации биоресурсов с учётом налогов и коррупции // Известия Южного федерального университета. Технические науки. — 2012. — № 6 (131). — С. 203–207.
94. Шедий М. В. Типология коррупции и основные модели коррупционных стратегий поведения // Научные ведомости Белгородского государственного университета. Серия: Философия. Социология. Право. — 2011. — № 8. — С. 86–96.
95. Южанин А. О. Транснациональная коррупция: глобальная проблема современности // Молодой ученый. — 2012. — № 5. — С. 351–353.
96. Balykina Y. E., Kolpak E. P., Kotina E. D. Mathematical model of thyroid function // Middle East Journal of Scientific Research. — 2014. — Т. 19. — № 3. — С. 429–433
97. Pronina Y. Analytical solution for the general mechanochemical corrosion of an ideal elastic-plastic thick-walled tube under pressure // International Journal of Solids and Structures. — 2013. — Т. 50. — № 22–23. — С. 3626–3633.
98. Pronina Y. G. Estimation of the life of an elastic tube under the action of a longitudinal force and pressure under uniform surface corrosion conditions // Russian metallurgy (Metally). — 2010. — Т. 2010. — № 4. — С. 361–364.
99. Zhukova I. V., Kolpak E. P., Balykina Yu. E. Mathematical Model of Growing Tumor // Applied Mathematical Sciences. — Vol. 9. — 2014. N 30. — 1455–1466.
