В настоящей работе изучается интегральный оператор, действующий в гильбертовом пространстве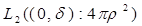 
функций квадратично интегрируемых по интервалу 
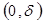с весом 
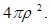Спектр этого оператора описан через спектр оператора типа Винера-Хопфа.
Ключевые слова: интегральный оператор, гильбертово пространство с весом, оператор типа Винера-Хопфа.
В последнее тридцатилетие значительно усилился интерес математиков к конкретным задачам, имеющим происхождение в теоретической физике. В результате заметно изменилось содержание традиционной математической физики. Наиболее популярным и традиционным объектом для математической физики служит нерелятивистская квантовая механика, точнее- оператор Шредингера. Более того, сам облик современной математической физики в значительной мере сформировался при изучении этого оператора. По сути дела вся атомная, молекулярная и значительная часть ядерной физики, физики плазмы и твердого тела состоит в изучении оператора Шредингера [1–3]. Поэтому исследование оператора Шредингера играет чрезвычайно важную роль в современной математике.
В спектральном анализе трехчастичного непрерывного и решетчатого оператора Шредингера имеется следующий замечательный результат:
если в системе тpех частиц, взаимодействующих с помощью паpных коpоткодействующих потенциалов, ни одна из тpех двухчастичных подсистем не имеет связанных состояний с отрицательной энергией, но по меньшей меpе две из них имеют pезонанс с энеpгией в нуле, то у этой тpехчастичной системе существует бесконечное число тpехчастичных связанных состояний с отpицательной энеpгией, накапливающихся к нулю. Этот эффект впеpвые был обнаpужен Ефимовым [4]. При доказательстве существование эффекта Ефимова для решетчатых моделей, в том числе для трехчастичного дискретного оператора Шредингера основной роль играет предельный оператор Фаддеева и показывается, что этот оператор имеет существенный спектр, лежащий правее точки 1. см. например [5–8]. В Данной работе рассматривается интегральный оператор, который получается при изучении спектра оператора Фаддеева соответствующих для некоторых моделей.
Рассмотрим оператор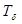 
действующий в 
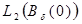по формуле
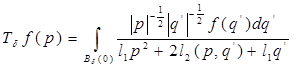
где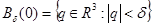 
, а 
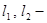положительные постоянные.
Тогда оператор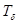 
имеет инвариантное подпространство, состоящее из сферически-симметричных функций. Действительно, есл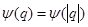и 
и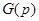 
поворот шара 
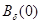в себя относительно нуля, то
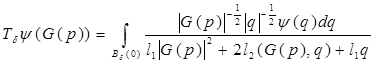
Сделав замену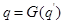 
и учитывая соотношения
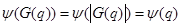
и
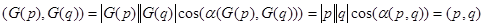
имеем, что
.
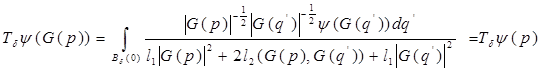Здесь через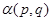 
обозначен угол между 
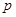и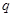 
. Отсюда следует, что функция 
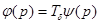зависит только от модуля 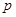, поэтому 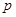выбираем 
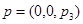. Теперь переходя к сферическим координатам
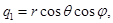
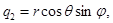
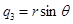
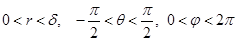
мы получим
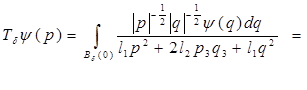
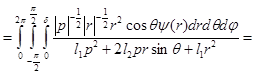
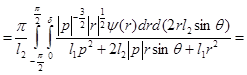
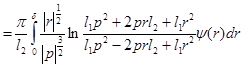
Можно считать, что «сферически-симметрическая» часть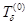 
оператора 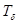является оператором, действующим в гильбертовом пространстве 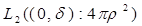функций квадратично интегрируемых по интервалу 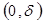с весом 
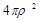. т. е.
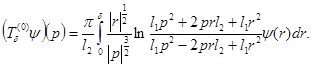
Пусть оператор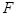 
действует из пространства 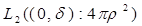в пространство 
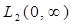по следующему правилу
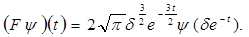
Оператор 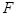сохраняет норму и его область значений совпадает со
всем пространством. Действительно,
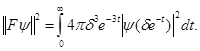
Сделав замену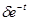 
мы получим, что
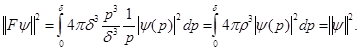
Лемма 1. Оператор 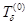унитарно эквивалантен оператору 
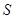действующему в 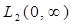по формуле
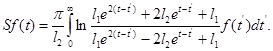
Доказательство. Унитарная эквивалентность операторов 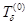и 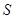осуществляется при помощи унитарного оператора 
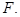Легко можно проверит, что 
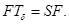Имеем
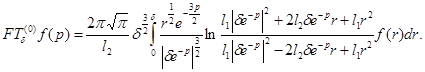
Сделая замену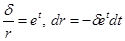 
получим, что
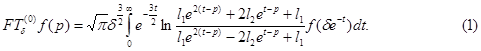
Теперь рассмотрим 
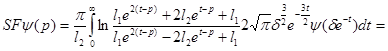
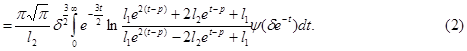
Из равенств (1) и (2) следует, что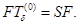 
Лемма 1 доказана.
В следующем утверждении, полученном Гохбергом и Крейном, дано описание спектра матричного оператора типа Винера-Хопфа.
Предложение 1. Пусть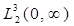 
гильбертово пространство трех- компонентных вектор функций 
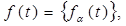где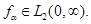 
Пусть оператор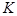 
действующий в 
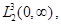определяется следующим образом: равенство 
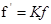означает, что
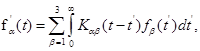
где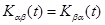 
и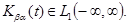 
Обозначим через 
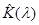симметричную трехрядную матрицу, элементы которой определяются соотношениями
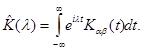
а через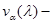 
собственные числа матрицы 
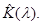Тогда 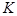является ограниченным самосопряженным оператором, спектр которого совпадает с множеством значений, принимаемых функциями 
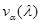при вещественных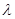
Из Предложения 1 вытекает следующее
Предложение 2. Оператор 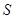является ограниченным, самосопряженным оператором, спектр которого совпадает с множеством значений, принимаемых функцией
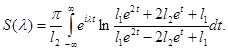
при вещественных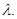 
Так как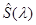 
непрерывна, то согласно предложению 2 получим следующее
Предложение 3. Если при некотором 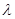число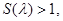 
то существенный спектр оператора 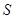содержит интервал расположенный правее точки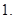 
Благодарности. Авторы выражают искреннюю благодарность Т. Х. Расулову за постановку задачи и за ценные обсуждение.
Литература:
1. Рид. М., Саймон.Б. Методы современной математической физики. Т.3. Теория рассеяния. М.: Мир. 1982.
2. Рид. М., Саймон.Б. Методы современной математической физики. Т.4. Анализ операторов. М.: Мир. 1982.
3. Меркурьев С. П.,Фаддеев Л. Д. Квантовая теория рассеяния для систем нескольких частиц. М.: Наука. 1985.
4. Efimov V. N. Energy levels arising from resonances two-body forces in a three-body system. Phys. Lett. 1970. B.33. No.8. pp.563–564.
5. Лакаев С. Н., Муминов М. Э., Существенный и дискретный спектр трехчастичного оператора Шредингера на решетке. Теор. и мат. физ., 135:3, (2003), 478–503.
6. Albeverio S., Lakaev S. N., Muminov Z. I., Schrődinger Operators on Lattices. The Efimov Effect and Discrete Spectrum Asymptotics. Ann. Henri Poincaré, 5, (2004), 743–772.
7. Albeverio S., Lakaev S. N., Rasulov T. H., On the Spectrum of an Hamiltonian in Fock Space. Discrete Spectrum Asymptotics. J. Stat. Phys., 127:2, (2007), 191–220.
8. Albeverio S., Lakaev S. N., Rasulov T. H., The Efimov Effect for a Model Operator Associated with the Hamiltonian of a non Conserved Number of Particles. Methods Func. Anal. Topol., 13:1, (2007), 1–16.
