В этой статье изложен метод решения линейных интегральных уравнений сведением к дифференциальным уравнениям в частных производных первого порядка с запаздывающим аргументом. Преимущество изучаемого метода в том, что он анализируется на примерах различной природы.
Ключевые слова: линейные интегральные уравнения, дифференциальные уравнения с запаздывающим аргументом, формула дифференцирования, частная производная, функциональный ряд.
Рассмотрим линейное интегральное уравнение
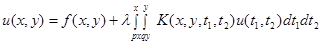, (1)
здесь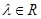 
, 
, 
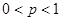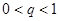— параметры, 
, 
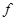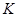известные функции определенные в 
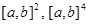, соответственно, 
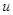определенная в 
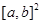неизвестная (или искомая) функция, допускается что все они имеют частные производные любого порядка. Основной целью статьи является сведение интегрального уравнения (1) к обыкновенному дифференциальному уравнению и его решению.
Для достижения этой цели используем формулу дифференцирования по параметру определенного интеграла с переменными пределами, т. е. формулу
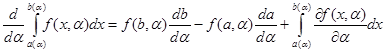. (2)
Здесь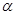 
-параметр, 
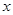— переменная интегрирования.
Для решения выше указанных интегральных уравнений, сведение их дифференциальным уравнениям создаёт возможность большего углублённого изучения интегральных уравнений. Согласно проводимым исследованиям решение дифференциальных уравнений в общем — то сложнее по отношению к решениям интегральных уравнений. Но для освещения некоторых вопросов во время исследования не исключена вероятность необходимости сведения заданного интегрального уравнению к заданному дифференциальному уравнению. Что интересно, в результате преобразования приходим к дифференциальному уравнению с запаздывающим аргументом [1].
Решению интегрального уравнения удовлетворяет соответствующее ему дифференциальное уравнение. Но решение дифференциального уравнения будет более общим, чем решение интегрального уравнения [1–8].
В этой статье познакомимся сведением интегральных уравнений (1) к дифференциальным уравнениям в частных производных. В результате приходим к дифференциальным уравнениям в частных производных с запаздывающим аргументом. Известно, что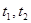 
в интегральном уравнении (1) переменные интегрирования, мы считаем, что 
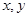параметрами и применяем формулу (2). Выполнение которых рассмотрим на примерах.
Пример 1. Следующее
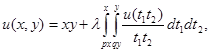
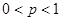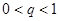, (3)
интегральное уравнение преобразуем к дифференциальному уравнению.
Сперва найдём производные обеих частей уравнения по параметру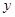 
соответственно по формуле (2):
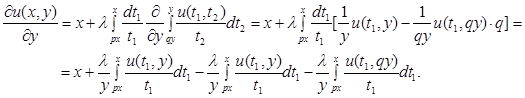
С целью избавления от последних двух интегралов, далее находим частные производные параметру 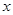после упрощений получим указанное ниже дифференциальное уравнение в частных производных:
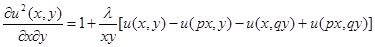. (4)
Здесь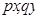 
-запаздывающие аргументы, а 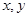простые аргументы (независимые переменные).
Решение уравнения (3) получим виде:
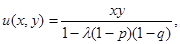(5)
здесь
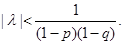
Пример 2. Следующее
(
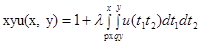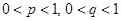) (6)
интегральное уравнение преобразуем к дифференциальному уравнению.
Сперва найдём производные обеих частей по параметру :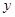
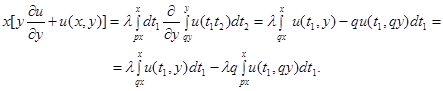
Теперь находим частные производные по параметру 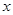, после упрощений получим:
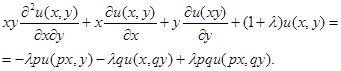(7)
Решение уравнения (6) получим виде:
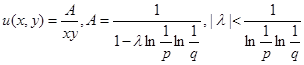. (8)
Ознакомимся с отдельными образцами дифференциальных уравнений в частных производных с запаздывающим аргументом. Такие уравнения встречаются в математической физике и технических науках.
Дифференциальные уравнения в частных производных первого порядка. Ищем решения дифференциальных уравнений в частных производных первого порядка в виде нижеследующего функционального ряда:
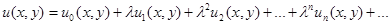. (9)
Здесь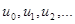 
пока неизвестные функции. Их определение означает нахождение решение задачи.
Пример 3. Задано следующее
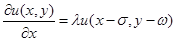(10)
дифференциальное уравнение с запаздывающим аргументом. Здесь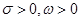 
- постоянные числа, 
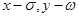запаздывающие аргументы, 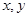простые аргументы (независимые переменные).
Считая, что решение записано в виде функционального ряда (9) подставим его в уравнение (10), в результате получим тождество:
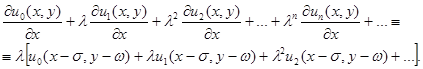
Приравниваем одинаковые степени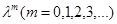 
обеих частях равенства:
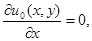здесь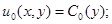 
.
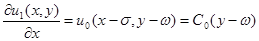Интегрируя его по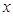 
в результате получим
.
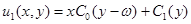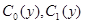— произвольные функции, не зависящее от параметра 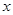. А также
.
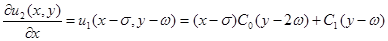Интегрируя его по 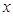получим
.
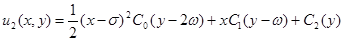Подобно этому
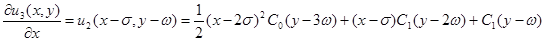
Отсюда
.
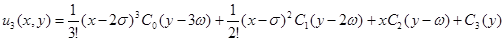Точно таким же методом можно найти нижеследующие:
.........................................
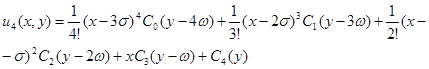
Теперь все найденные значения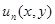 
подставим в ряд (9), в результате имеем:
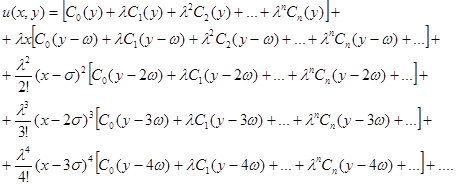
Обозначим:
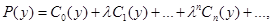
тогда можно записать
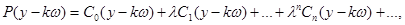
(здесь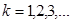 
). Значит решение можно записать в следующем виде:
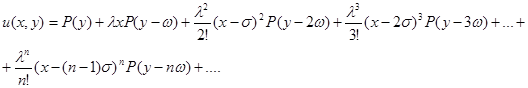(11)
Теперь выводим некоторые частные решения этого уравнения (11):
а) Пусть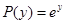 
, тогда
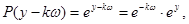
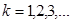
Из решения (11)
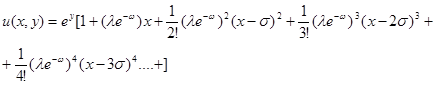(12)
б) Пусть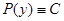 
будет произвольным постоянным числом, тогда
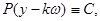к=1,2,3,…
из решения (11) имеем:
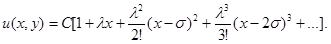(13)
Примечание. В частном случае в уравнении (10) возможно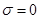 
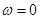или 
или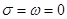 
. В этих случаях, соответственно этим случаям решение (11) более упрощается.
Пример 4. Задано дифференциальное уравнение
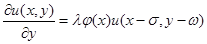(14)
с запаздывающими аргументами. Здесь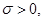 
, 
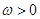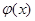-заданная функция.
И в это же уравнение подставляем ряд (9), потом в полученном тождестве путем приравнивания коэффициентов находим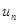 
:
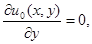здесь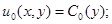
.
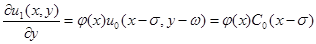Отсюда
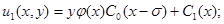
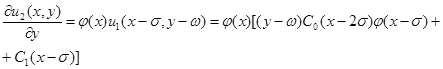
или
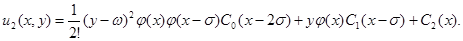
Точно таким же способом можно найти
..............................................
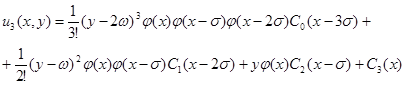
Подставляя их в ряд (9) можно записать:
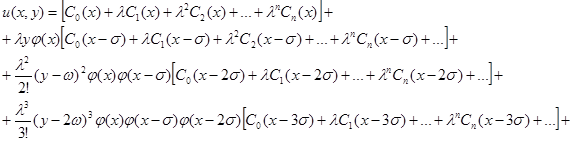
Введем следующее обозначение:
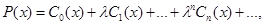
отсюда
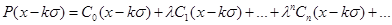
(здесь 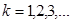). Тогда решение приходит к простому виду:
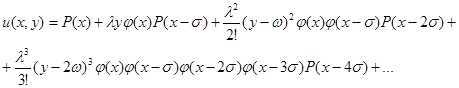(15)
Здесь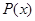 
произвольная функция переменной .
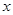При различных конкретных видах 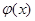и 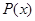, из (15) можно получить различные частные решения. Допустим
,
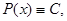
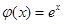тогда
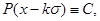
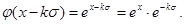
Поэтому из (15) получим нижеследующее частные решение:
.
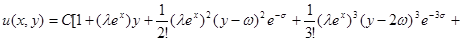
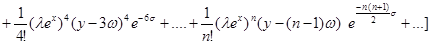Литература:
1. Ш. Т. Максудов. Элементы линейных интегральных уравнений. Ташкент, 1975 (на узбекском языке).
2. И. И. Привалов. Интегральные уравнение. Гостехиздат, М. 1935.
3. У. В. Ловитт. Линейные интегральные уравнение. Гостехиздат, М. 1957.
4. С. Г. Михлин. Лекции по линейным интегральным уравнениям. Гостехиздат М. 1959.
5. В. К. Кабулов. Интегральные уравнение типа баланса. «Фан» Т. 1961
6. А. Н. Филатов. Методы усреднения в дифференциальных и интегро- дифференциальных уравнениях. «Фан» Т. 1971.
7. С. П. Тимошенко. Колебания в инженерном деле. «Наука» М. 1967.
8. M. Л. Краснов, A. И. Киселев, Г. И. Макаренко. Сборник задач по обыкновенным дифференциалным уравнениям.-M: Высшая школа,1978.
