Эта статья посвящена изложению метода решения линейных интегральных уравнений сведением к дифференциальным уравнениям в частных производных высшего порядка с запаздывающим аргументом. Преимущество изучаемого метода анализируется на примерах различной природы.
Ключевые слова: линейные интегральные уравнения, дифференциальные уравнения, запаздывающие аргументы, частные производные высшего порядка, функциональный ряд.
Некоторые процессы не могут быть адекватно описаны обыкновенными дифференциальными уравнениями (т. е. уравнениями, в которые значения неизвестной функции и ее производных входит при одном и том же значении независимой переменной («времени»)). В связи с этим возникает необходимость рассматривать уравнения, в которых неизвестная функция входит при различных значениях аргумента. Одним из представителей таких уравнений является простейшее дифференциальное уравнение с запаздывающим аргументом или дифференциально-разностное уравнение вида
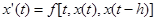 , (1)
, (1)
в котором 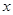 -неизвестная функция независимого аргумента
-неизвестная функция независимого аргумента 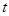 ,
, 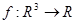 , а
, а 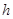 - положительное число (запаздывание). Таким образом, в уравнении (1) значение производной неизвестной функции в момент времени
- положительное число (запаздывание). Таким образом, в уравнении (1) значение производной неизвестной функции в момент времени 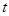 определяется не только тем как ведет себя сама функция в это время (как это было в обыкновенных дифференциальных уравнениях), но и тем как она вела себя в предыдущий момент времени
определяется не только тем как ведет себя сама функция в это время (как это было в обыкновенных дифференциальных уравнениях), но и тем как она вела себя в предыдущий момент времени 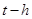 ("
("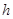 секунд назад»).
секунд назад»).
Простейшим примером процесса, описываемого дифференциальным уравнением с запаздывающим аргументом, может служить уравнение развития биологической популяции. Если считать, что скорость прироста популяции пропорциональна ее численности 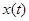 в настоящий момент, то мы получим известное уравнение Мальтуса или уравнение мальтузианского роста
в настоящий момент, то мы получим известное уравнение Мальтуса или уравнение мальтузианского роста
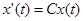 .
.
Если же исходить из (более реального) предположения о том, что скорость прироста пропорциональна численности лишь половозрелых особей (скажем, имеющих не меньший, чем h возраст), то мы придем к дифференциально-разностному уравнению
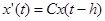 ,
,
поскольку величина 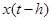 , равная численности популяции в момент
, равная численности популяции в момент 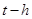 , как раз и описывает численность взрослых особей родившихся "
, как раз и описывает численность взрослых особей родившихся "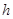 лет назад».
лет назад».
Одним из главных отличий дифференциальных уравнений с запаздывающим аргументом от обыкновенных дифференциальных уравнений является тот факт, что решения первых, вообще говоря, не допускают продолжения влево от начального отрезка, тогда как для вторых положительное и отрицательное направления времени полностью равноправны.
Рассмотрим линейное интегральное уравнение
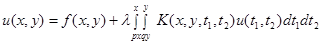 , (2)
, (2)
здесь 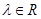 ,
, 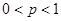 ,
, 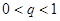 — параметры,
— параметры, 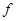 ,
, 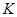 известные функции определенные в
известные функции определенные в 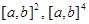 , соответственно,
, соответственно, 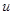 определенная в
определенная в 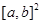 неизвестная (или искомая) функция, допускается что все они имеют частные производные любого порядка.
неизвестная (или искомая) функция, допускается что все они имеют частные производные любого порядка.
В этой статье познакомимся сведением интегральных уравнений (2) к дифференциальным уравнениям в частных производных [1–8]. В результате приходим к дифференциальным уравнениям в частных производных с запаздывающим аргументом [1]. Известно, что 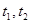 в интегральном уравнении (1) переменные интегрирования, мы считаем, что
в интегральном уравнении (1) переменные интегрирования, мы считаем, что 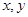 параметрами. Рассмотрим на примерах.
параметрами. Рассмотрим на примерах.
Пример 1. Следующее интегральное уравнение
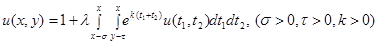 (3)
(3)
преобразуем к дифференциальному уравнению.
Сначала найдём частное производное по 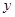 :
:
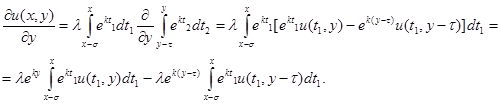
Теперь находя с обоих сторон частную производную по 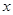 , после упрощений получим нижеследующее дифференциальное уравнение:
, после упрощений получим нижеследующее дифференциальное уравнение:
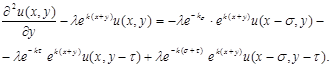
Здесь 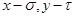 запаздывающие аргументы. Тогда
запаздывающие аргументы. Тогда

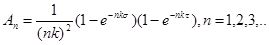 (4)
(4)
будет решением заданного интегрального уравнения (3).
Ознакомимся с отдельными образцами дифференциальных уравнений в частных производных высших порядков с запаздывающим аргументом. Такие уравнения встречаются в математической физике и технических науках.
Дифференциальные уравнения в частных производных высших порядков. Решения дифференциальных уравнений в частных производных высших порядков ищем в виде нижеследующего функционального ряда:
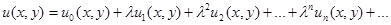 (5)
(5)
Здесь 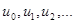 пока неизвестные функции. Их определение означает нахождение решение задачи. Процесс решения дифференциальных уравнений высших порядков рассмотрим на примерах.
пока неизвестные функции. Их определение означает нахождение решение задачи. Процесс решения дифференциальных уравнений высших порядков рассмотрим на примерах.
Пример 2. Пусть требуется решить следующее:
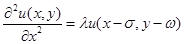 (6)
(6)
дифференциальное уравнение высокого порядка. Здесь 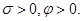
Подставим в это уравнение ряд (5), из полученного тождества путём приравнивания коэффициентов находим 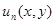 :
:
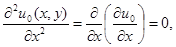 отсюда
отсюда 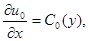
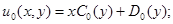
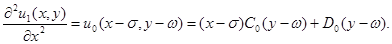
Отсюда в результате двухразового интегрирования по 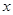 вытекает следующее:
вытекает следующее:
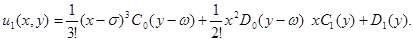
Таким способом можно найти
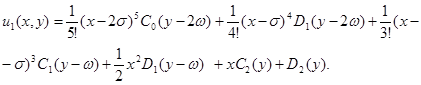
............................................
Найденные выражения 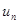 подставив в ряд (5), полученное решение можно записать в виде:
подставив в ряд (5), полученное решение можно записать в виде:
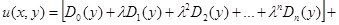
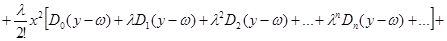
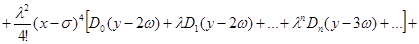
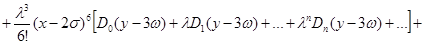
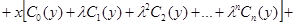
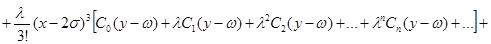
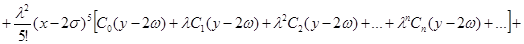
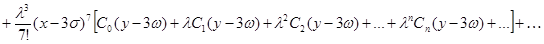
Примем обозначения:
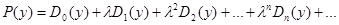
и
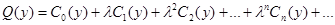
отсюда
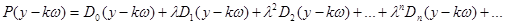
и
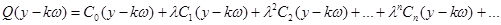
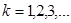
В этом случае решение примет вид:
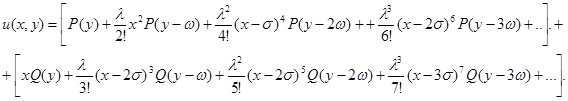 (7)
(7)
В решении 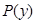 и
и 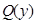 любые независящие от
любые независящие от 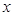 функции.
функции.
Например, если взять
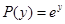 ,
, 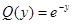 ,
,
то из (7) получим единственное частное решение.
Пример 3. Пусть требуется решить следующее
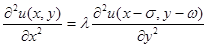 . (8)
. (8)
дифференциальное уравнение в частных производных высших порядков. Здесь 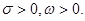
Подставив в это уравнение ряд (5) получим тождество, потом методом приравнивания коэффициентов находим 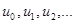 :
:
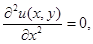 отсюда
отсюда 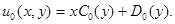
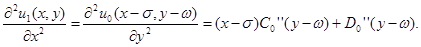
Интегрируем его два раза по 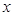 , тогда получим
, тогда получим
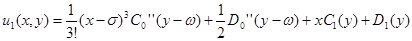 .
.
А также
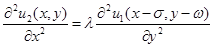 .
.
Здесь подставляя в правую часть значение выражения 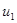 и проинтегрировав два раза по
и проинтегрировав два раза по 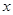 получим:
получим:
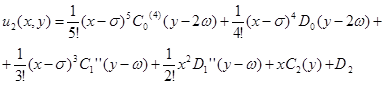
...................................................
Теперь подставив эти выражения 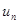 в ряд (5) запишем его виде:
в ряд (5) запишем его виде:
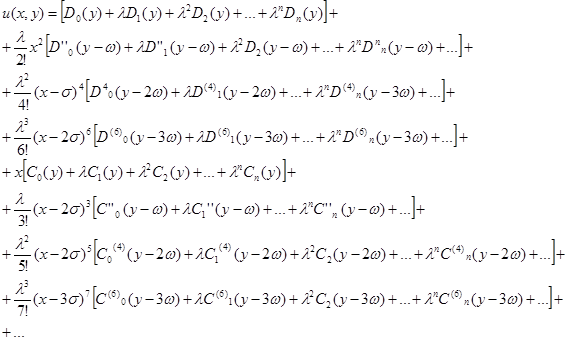
Примем обозначения:
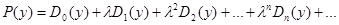
и
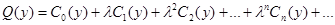
Допускаем возможность нахождения производных любого порядка от них. Тогда решение примет вид:
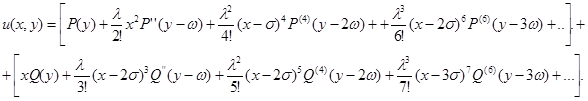 (9)
(9)
В этом решение 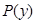 и
и 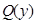 произвольные функции производные высших порядков которых существуют. В частном случае может случиться, что
произвольные функции производные высших порядков которых существуют. В частном случае может случиться, что 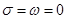 , тогда общее решение (9) уравнения (8) более упрощается.
, тогда общее решение (9) уравнения (8) более упрощается.
Литература:
1. Ш. Т. Максудов. Элементы линейных интегральных уравнений. Ташкент, 1975 (на узбекском языке).
2. И. И. Привалов. Интегральные уравнение. Гостехиздат, М. 1935.
3. У. В. Ловитт. Линейные интегральные уравнение. Гостехиздат, М. 1957.
4. С. Г. Михлин. Лекции по линейным интегральным уравнениям. Гостехиздат М. 1959.
5. В. К. Кабулов. Интегральные уравнение типа баланса. «Фан» Т. 1961
6. А. Н. Филатов. Методы усреднения в дифференциальных и интегро- дифференциальных уравнениях. «Фан» Т. 1971.
7. С. П. Тимошенко. Колебания в инженерном деле. «Наука» М. 1967.
8. M. Л. Краснов, A. И. Киселев, Г. И. Макаренко. Сборник задач по обыкновенным дифференциальным уравнениям.-M: Высшая школа,1978.







