В статье изучаются свойства n-кратно Ω-расслоенных формаций конечных групп. Установлена взаимосвязь между τ-замкнутостью 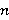 -кратно Ω-расслоенной формации с bnr-направлением
-кратно Ω-расслоенной формации с bnr-направлением  и τ-замкнутостью ее
и τ-замкнутостью ее  -спутника в случае, когда
-спутника в случае, когда 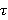 — регулярный
— регулярный 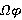 -радикальный подгрупповой функтор, замкнутый относительно композиционных факторов.
-радикальный подгрупповой функтор, замкнутый относительно композиционных факторов.
Ключевые слова:конечная группа, класс групп, формация групп, Ω-расслоенная формация, подгрупповой функтор.
Теория формаций конечных групп представляет собой один из важных разделов современной теории классов групп. Понятие формации было введено В. Гашюцем в 1963 году [1]. Формации представляют собой классы групп, замкнутые относительно гомоморфных образов и подпрямых произведений. Ключевые результаты о формациях конечных групп представлены в монографиях Л. А. Шеметкова [2] и А. Н. Скибы [3]. При построении формаций важную роль играют функциональные методы. Так, например, в основе построения локальных и композиционных формаций, наиболее изученных в настоящее время, лежат функции, называемые в [2] экранами. В 1999 году В. А. Ведерников разработал новый функциональный подход к исследованию формаций групп, основанный на рассмотрении для них двух сопутствующих функций — функции-спутника и функции-направления [4]. Введенное в работе [4] понятие Ω-расслоенной формации является естественным обобщением понятия локальной формации, а композиционные формации представляют один из видов Ω-расслоенных формаций.
В последние годы была выявлена тесная связь между подгрупповыми функторами и классами конечных групп (см., например, [5]). Большую роль в этом направлении играют τ-замкнутые формации, то есть такие формации, которые вместе с каждой своей группой содержат и все ее 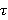 -подгруппы. В настоящей работе рассматриваются τ-замкнутые формации для регулярного подгруппового функтора
-подгруппы. В настоящей работе рассматриваются τ-замкнутые формации для регулярного подгруппового функтора 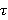 , замкнутого относительно композиционных факторов.
, замкнутого относительно композиционных факторов.
Хорошо известно, что свойства локальных, композиционных, Ω-расслоенных формаций во многих случаях зависят от свойств их спутников (см., например, [4, 6, 7]). В этой связи интерес представляет изучение свойств спутников τ-замкнутых n-кратно Ω-расслоенных формаций. Целью данной работы является исследование взаимосвязи между τ-замкнутостью n-кратно Ω-расслоенной формации с bnr-направлением  и τ-замкнутостью ее
и τ-замкнутостью ее  -спутника.
-спутника.
1. Основные определения, обозначения и предварительные результаты
Рассматриваются только конечные группы. Используются определения и обозначения, принятые в [2, 4, 5]. Приведем лишь некоторые из них.
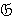 — класс всех конечных групп.
— класс всех конечных групп.
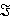 — класс всех конечных простых групп.
— класс всех конечных простых групп.
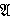 — класс всех конечных абелевых групп.
— класс всех конечных абелевых групп.
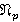 — класс всех конечных p-групп.
— класс всех конечных p-групп.
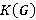 — класс всех простых групп, изоморфных композиционным факторам группы
— класс всех простых групп, изоморфных композиционным факторам группы 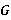 ;
; 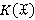 — объединение классов
— объединение классов 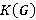 для всех
для всех 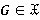 .
.
Ω — непустой подкласс класса 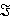 .
.
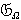 — класс всех конечных Ω-групп, т. е. таких групп, для которых
— класс всех конечных Ω-групп, т. е. таких групп, для которых 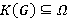 .
.
Пусть  — формация групп. F-корадикалом группы
— формация групп. F-корадикалом группы 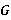 называется пересечение всех тех нормальных подгрупп группы
называется пересечение всех тех нормальных подгрупп группы 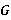 , факторгруппы по которым принадлежат
, факторгруппы по которым принадлежат  , и обозначается
, и обозначается 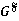 .
.
Пусть  — класс Фиттинга. F-радикалом группы
— класс Фиттинга. F-радикалом группы 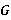 называется произведение всех нормальных подгрупп группы
называется произведение всех нормальных подгрупп группы 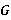 , принадлежащих
, принадлежащих  , и обозначается
, и обозначается 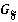 .
.
Пусть 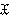 — класс групп,
— класс групп,  — формация групп. Корадикальным произведением классов
— формация групп. Корадикальным произведением классов 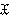 и
и  называется класс
называется класс 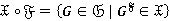 .
.
Пусть 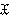 ,
, 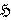 — классы групп. Гашюцевым произведением классов
— классы групп. Гашюцевым произведением классов 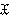 и
и 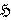 называется класс
называется класс 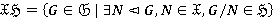 .
.
Функция 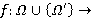 {формации групп} называется ΩF-функцией; функция
{формации групп} называется ΩF-функцией; функция 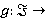 {формации групп} называется F-функцией; функция
{формации групп} называется F-функцией; функция 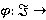 {непустые формации Фиттинга} называется FR-функцией. Функции
{непустые формации Фиттинга} называется FR-функцией. Функции  ,
, 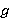 и
и  принимают одинаковые значения на изоморфных группах из области определения [4, с. 126].
принимают одинаковые значения на изоморфных группах из области определения [4, с. 126].
Формация 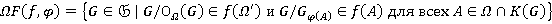 называется Ω-расслоенной формацией с Ω-спутником
называется Ω-расслоенной формацией с Ω-спутником  и направлением
и направлением  ; формация
; формация 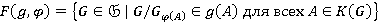 называется расслоенной формацией со спутником
называется расслоенной формацией со спутником 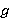 и направлением
и направлением  [4, с. 127].
[4, с. 127].
Направление  Ω-расслоенной формации называется b-направлением, если
Ω-расслоенной формации называется b-направлением, если 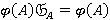 для любой абелевой группы
для любой абелевой группы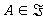 ; n-направлением, если
; n-направлением, если 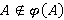 для любой неабелевой группы
для любой неабелевой группы 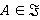 ; r-направлением, если
; r-направлением, если 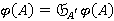 для любой группы
для любой группы 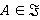 ;
; 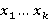 -направлением, если
-направлением, если  является
является 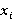 -направлением для любого
-направлением для любого 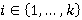 [7, с. 218].
[7, с. 218].
Через 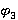 обозначается направление Ω-композиционной формации, т. е.
обозначается направление Ω-композиционной формации, т. е. 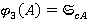 для любого
для любого 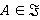 , где
, где 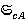 — класс всех конечных групп, у которых каждый главный А-фактор централен [4, с. 128].
— класс всех конечных групп, у которых каждый главный А-фактор централен [4, с. 128].
Ω-спутник  Ω-расслоенной формации
Ω-расслоенной формации  называется внутренним, если
называется внутренним, если 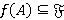 для любой группы
для любой группы 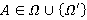 ; минимальным Ω-спутником формации
; минимальным Ω-спутником формации  , если
, если  является минимальным элементом множества всех Ω-спутников формации
является минимальным элементом множества всех Ω-спутников формации  .
.
Пусть 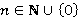 ,
,  — некоторая FR-функция. Всякая формация считается 0-кратно Ω-расслоенной формацией с направлением
— некоторая FR-функция. Всякая формация считается 0-кратно Ω-расслоенной формацией с направлением  . Формация
. Формация  называется n-кратно
называется n-кратно 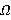 -расслоенной с направлением
-расслоенной с направлением  , или, иначе,
, или, иначе,  -расслоенной формацией, если
-расслоенной формацией, если  обладает
обладает  -спутником, т. е. таким Ω-спутником, всякое значение которого является
-спутником, т. е. таким Ω-спутником, всякое значение которого является 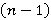 -кратно Ω-расслоенной формацией с направлением
-кратно Ω-расслоенной формацией с направлением  [7, с. 218].
[7, с. 218].
Пусть 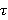 — отображение, которое ставит в соответствие всякой группе
— отображение, которое ставит в соответствие всякой группе 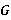 некоторую систему
некоторую систему 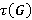 ее подгрупп. Отображение
ее подгрупп. Отображение 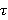 называется подгрупповым функтором, если
называется подгрупповым функтором, если 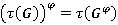 для любого изоморфизма
для любого изоморфизма  каждой группы
каждой группы 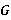 [5, с. 13]. Подгрупповой функтор
[5, с. 13]. Подгрупповой функтор 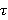 называется регулярным, если выполняются два условия: 1)
называется регулярным, если выполняются два условия: 1) 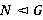 ,
, 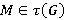
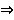
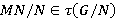 ; 2)
; 2) 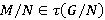
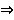
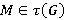 [5, с. 14]. Подгрупповой функтор
[5, с. 14]. Подгрупповой функтор 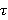 называется Ω-радикальным, если для любой группы
называется Ω-радикальным, если для любой группы 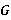 и для любой
и для любой 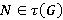 справедливо
справедливо 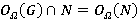 ; φ-радикальным, если для любой группы
; φ-радикальным, если для любой группы 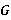 и для любой
и для любой 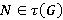 для всех
для всех 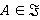 выполняется
выполняется 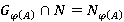 ; Ωφ-радикальным, если
; Ωφ-радикальным, если 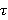 является Ω-радикальным и
является Ω-радикальным и  -радикальным [10, с. 76]. Подгрупповой функтор
-радикальным [10, с. 76]. Подгрупповой функтор 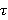 называется замкнутым относительно композиционных факторов, если для любой
называется замкнутым относительно композиционных факторов, если для любой 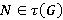 справедливо включение
справедливо включение 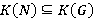 для каждой группы
для каждой группы 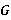 [10, с. 76].
[10, с. 76].
Формация  называется τ-замкнутой, если
называется τ-замкнутой, если 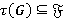 для любой группы
для любой группы 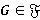 [3, с. 23]. Ω-спутник Ω-расслоенной формации
[3, с. 23]. Ω-спутник Ω-расслоенной формации  называется τ-замкнутым, если все его значения являются τ-замкнутыми формациями.
называется τ-замкнутым, если все его значения являются τ-замкнутыми формациями.
Лемма 1.1 [4, лемма 5]. Пусть  — произвольная FR-функция,
— произвольная FR-функция, 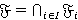 , где
, где 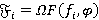 ,
, 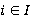 . Тогда
. Тогда 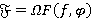 , где
, где 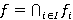 .
.
Лемма 1.2 [4, лемма 3]. Пусть 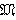 — формация,
— формация, 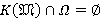 . Тогда
. Тогда 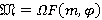 , где
, где 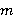 —
— 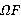 -функция такая, что
-функция такая, что 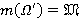 ,
, 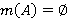 для всех
для всех 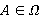 ,
,  — произвольная FR-функция. В частности, формации
— произвольная FR-функция. В частности, формации 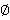 и
и 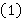 являются Ω-расслоенными формациями для любого непустого класса
являются Ω-расслоенными формациями для любого непустого класса 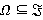 .
.
Лемма 1.3 [7, лемма 3]. Пусть 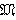 и
и 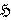 — Ω-расслоенные формации с r-направлением
— Ω-расслоенные формации с r-направлением  ,
, 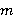 и
и 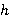 — внутренние Ω-спутники формаций
— внутренние Ω-спутники формаций 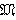 и
и 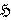 соответственно. Если
соответственно. Если 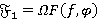 с внутренним Ω-спутником
с внутренним Ω-спутником  таким, что
таким, что 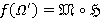 ,
, 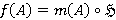 для всех
для всех 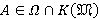 и
и 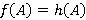 для всех
для всех 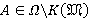 , то
, то 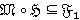 и
и  является внутренним Ω-спутником формации
является внутренним Ω-спутником формации 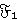 .
.
Лемма 1.4 [4, лемма 4]. Пусть 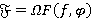 , где
, где  — произвольная FR-функция. Тогда: 1)
— произвольная FR-функция. Тогда: 1) 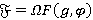 , где
, где 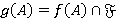 для любого
для любого 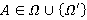 ; 2)
; 2) 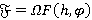 , где
, где 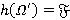 и
и 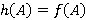 для любого
для любого 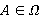 .
.
Лемма 1.5 [7, следствие 3]. Пусть  — Ω-расслоенная формация с внутренним Ω-спутником
— Ω-расслоенная формация с внутренним Ω-спутником  и br-направлением
и br-направлением  . Тогда: 1)
. Тогда: 1) 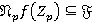 для всех
для всех 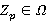 ; 2)
; 2)  обладает внутренним Ω-спутником
обладает внутренним Ω-спутником 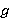 таким, что
таким, что 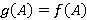 для всех
для всех 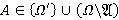 и
и 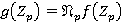 для всех
для всех 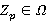 .
.
Лемма 1.6 [9, теорема 5.38]. Если 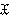 —
— 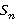 -замкнутый класс групп,
-замкнутый класс групп, 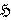 — формация, то
— формация, то 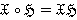 .
.
Лемма 1.7 [8, следствие 5.8]. Пусть  — внутренний Ω-спутник Ω-расслоенной формации
— внутренний Ω-спутник Ω-расслоенной формации  с br-направлением
с br-направлением  , удовлетворяющим условию
, удовлетворяющим условию 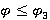 . Тогда формация
. Тогда формация  обладает единственным максимальным внутренним Ω-спутником
обладает единственным максимальным внутренним Ω-спутником 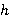 , причем
, причем 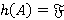 для всех
для всех 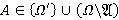 и
и 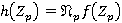 для всех
для всех 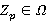 .
.
2. Свойства 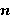 -кратно
-кратно 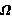 -расслоенных формаций
-расслоенных формаций
Лемма 2.1. Если  —
—  -расслоенная формация, то
-расслоенная формация, то  —
—  -расслоенная формация для любого
-расслоенная формация для любого 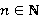 .
.
Доказательство. Докажем лемму методом математической индукции.
1. Установим справедливость утверждения при 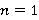 . Действительно, если
. Действительно, если  — Ω-расслоенная формация с направлением
— Ω-расслоенная формация с направлением  , то
, то  — формация. Это означает, что
— формация. Это означает, что  — 0-кратно Ω-расслоенная формация с направлением
— 0-кратно Ω-расслоенная формация с направлением  .
.
2. Предположим, что при 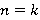 утверждение верно.
утверждение верно.
3. Покажем, что утверждение верно при 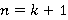 . Пусть
. Пусть  —
— 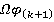 -расслоенная формация. Тогда по определению n-кратно Ω-расслоенной формации
-расслоенная формация. Тогда по определению n-кратно Ω-расслоенной формации  обладает
обладает 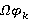 -спутником
-спутником  , то есть таким Ω-спутником
, то есть таким Ω-спутником  , все значения которого являются
, все значения которого являются 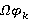 -расслоенными формациями. Согласно предположению индукции, все значения
-расслоенными формациями. Согласно предположению индукции, все значения  являются
являются 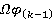 -расслоенными формациями. Следовательно,
-расслоенными формациями. Следовательно,  является
является 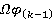 -спутником формации
-спутником формации  , и значит,
, и значит,  —
— 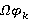 -расслоенная формация. Итак, утверждение верно при
-расслоенная формация. Итак, утверждение верно при 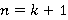 .
.
Из пунктов 1–3 по методу математической индукции утверждение верно для любого 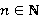 . Лемма доказана.
. Лемма доказана.
Следствие 2.1.1. Если  — n-кратно расслоенная формация с направлением
— n-кратно расслоенная формация с направлением  , то
, то  —
— 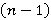 -кратно расслоенная формация с направлением
-кратно расслоенная формация с направлением  для любого
для любого 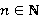 .
.
В следующих леммах приводятся примеры n-кратно Ω-расслоенных формаций.
Лемма 2.2. Пусть  —
— 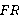 -функция. Тогда формации
-функция. Тогда формации 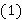 и
и 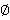 являются
являются  -расслоенными формациями для любого
-расслоенными формациями для любого 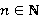 .
.
Доказательство. Докажем лемму методом математической индукции.
1. Установим справедливость утверждения при 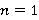 . Действительно, по лемме 1.2 формации
. Действительно, по лемме 1.2 формации 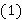 и
и 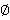 являются Ω-расслоенными формациями с направлением
являются Ω-расслоенными формациями с направлением  .
.
2. Предположим, что при 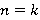 утверждение верно.
утверждение верно.
3. Покажем, что утверждение верно при 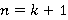 .
.
Пусть 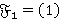 . Согласно лемме 1.2,
. Согласно лемме 1.2, 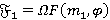 , где
, где 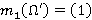 и
и 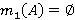 для любого
для любого 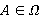 . По предположению индукции формации
. По предположению индукции формации 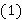 и
и 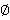 являются
являются 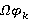 -расслоенными формациями. Следовательно,
-расслоенными формациями. Следовательно, 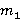 является
является 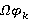 -спутником формации
-спутником формации 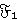 , и значит,
, и значит, 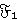 —
— 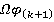 -расслоенная формация.
-расслоенная формация.
Пусть 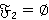 . Согласно лемме 1.2,
. Согласно лемме 1.2, 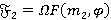 , где
, где 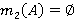 для любого
для любого 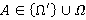 . По предположению индукции формация
. По предположению индукции формация 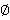 является
является 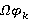 -расслоенной формацией. Следовательно,
-расслоенной формацией. Следовательно, 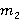 является
является 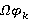 -спутником формации
-спутником формации 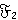 , и значит,
, и значит, 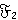 —
— 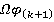 -расслоенная формация.
-расслоенная формация.
Из пунктов 1–3 по методу математической индукции утверждение верно для любого 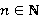 . Лемма доказана.
. Лемма доказана.
Следствие 2.2.1. Пусть  — FR-функция. Тогда формации
— FR-функция. Тогда формации 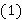 и
и 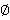 являются n-кратно расслоенными формациями с направлением
являются n-кратно расслоенными формациями с направлением  для любого
для любого 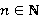 .
.
Лемма 2.3. Пусть 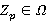 ,
,  — b-направление Ω-расслоенной формации. Тогда формация
— b-направление Ω-расслоенной формации. Тогда формация 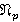 является
является  -расслоенной формацией для любого
-расслоенной формацией для любого 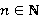 .
.
Доказательство. Докажем лемму методом математической индукции.
1. Установим справедливость утверждения при 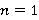 , то есть покажем, что
, то есть покажем, что 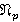 — Ω-расслоенная формация с направлением
— Ω-расслоенная формация с направлением  . Пусть
. Пусть 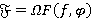 , где
, где 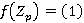 ,
, 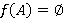 для любого
для любого 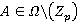 ,
, 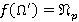 . Докажем, что
. Докажем, что 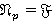 .
.
Пусть 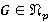 . Так как
. Так как 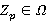 , то
, то 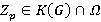 . Поскольку
. Поскольку  является b-направлением, то
является b-направлением, то 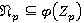 , и значит,
, и значит, 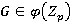 . Тогда
. Тогда 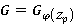 и
и 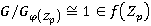 . Так как
. Так как 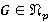 и
и 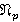 — формация, то
— формация, то 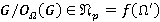 . Следовательно,
. Следовательно, 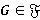 и
и 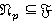 .
.
Допустим, что 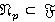 и
и 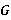 — группа наименьшего порядка из
— группа наименьшего порядка из 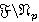 . Тогда
. Тогда 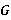 — монолитическая группа с монолитом
— монолитическая группа с монолитом 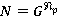 . Пусть
. Пусть 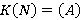 . Если
. Если 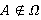 , то
, то 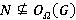 и
и 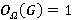 . Так как
. Так как 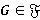 , то
, то 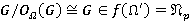 . Противоречие. Пусть
. Противоречие. Пусть 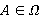 . Тогда
. Тогда 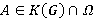 и, ввиду
и, ввиду 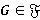 , получаем
, получаем 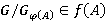 . Следовательно,
. Следовательно, 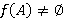 . Из строения Ω-спутника
. Из строения Ω-спутника  следует, что
следует, что 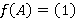 , и значит,
, и значит, 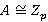 и
и 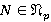 . Тогда, в силу
. Тогда, в силу 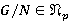 , имеем
, имеем 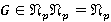 . Противоречие. Следовательно,
. Противоречие. Следовательно, 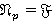 , и поэтому
, и поэтому 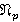 — Ω-расслоенная формация с направлением
— Ω-расслоенная формация с направлением  .
.
2. Предположим, что при 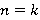 утверждение верно.
утверждение верно.
3. Покажем, что утверждение верно при 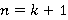 . В пункте 1 доказано, что
. В пункте 1 доказано, что 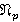 совпадает с формацией
совпадает с формацией  , которая обладает Ω-спутником
, которая обладает Ω-спутником  , имеющим следующее строение:
, имеющим следующее строение: 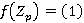 ,
, 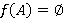 для любого
для любого 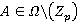 ,
, 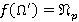 . Так как, учитывая лемму 2.2 и предположение индукции, все значения Ω-спутника
. Так как, учитывая лемму 2.2 и предположение индукции, все значения Ω-спутника  являются
являются 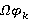 -расслоенными формациями, то
-расслоенными формациями, то 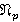 —
— 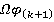 -расслоенная формация.
-расслоенная формация.
Из пунктов 1–3 по методу математической индукции утверждение верно для любого 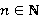 . Лемма доказана.
. Лемма доказана.
В лемме 1.1 доказано, что пересечение любой совокупности Ω-расслоенных формаций с направлением  является Ω-расслоенной формацией с направлением
является Ω-расслоенной формацией с направлением  . Следующее утверждение является обобщением данного результата для τ-замкнутых n-кратно Ω-расслоенных формаций.
. Следующее утверждение является обобщением данного результата для τ-замкнутых n-кратно Ω-расслоенных формаций.
Лемма 2.4. Пусть 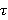 — подгрупповой функтор,
— подгрупповой функтор,  — FR-функция. Тогда пересечение любой совокупности τ-замкнутых
— FR-функция. Тогда пересечение любой совокупности τ-замкнутых  -расслоенных формаций является τ-замкнутой
-расслоенных формаций является τ-замкнутой  -расслоенной формацией для любого
-расслоенной формацией для любого 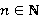 .
.
Доказательство. Пусть 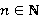 ,
, 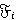 — τ-замкнутая
— τ-замкнутая  -расслоенная формация,
-расслоенная формация, 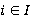 , и
, и 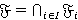 . Покажем, что
. Покажем, что  — τ-замкнутая
— τ-замкнутая  -расслоенная формация.
-расслоенная формация.
1) Покажем, что  — τ-замкнутая формация. Пусть
— τ-замкнутая формация. Пусть 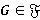 . Тогда
. Тогда 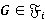 для любого
для любого 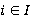 . Так как
. Так как 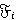 — τ-замкнутая формация, то
— τ-замкнутая формация, то 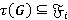 для любого
для любого 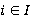 . Следовательно,
. Следовательно, 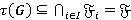 и
и  является τ-замкнутой формацией.
является τ-замкнутой формацией.
2) Методом математической индукции докажем, что  —
—  -расслоенная формация.
-расслоенная формация.
1. Установим справедливость утверждения при 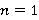 . Действительно, если
. Действительно, если 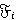 — Ω-расслоенная формация с направлением
— Ω-расслоенная формация с направлением  ,
, 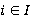 , то по лемме 1.1
, то по лемме 1.1 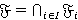 — Ω-расслоенная формация с направлением
— Ω-расслоенная формация с направлением  .
.
2. Предположим, что при 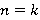 утверждение верно.
утверждение верно.
3. Покажем, что утверждение верно при 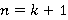 . Пусть
. Пусть 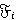 —
— 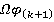 -расслоенная формация,
-расслоенная формация, 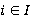 . Тогда
. Тогда 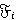 обладает
обладает 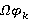 -спутником
-спутником 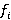 , то есть таким спутником
, то есть таким спутником 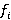 , все значения которого являются
, все значения которого являются 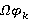 -расслоенными формациями,
-расслоенными формациями, 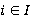 . Пусть
. Пусть  — такая ΩF-функция, что
— такая ΩF-функция, что 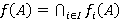 для любого
для любого 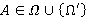 . Тогда, согласно предположению индукции, все значения Ω-спутника
. Тогда, согласно предположению индукции, все значения Ω-спутника  являются
являются 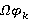 -расслоенными формациями. По лемме 1.1
-расслоенными формациями. По лемме 1.1 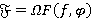 . Следовательно,
. Следовательно,  —
— 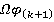 -расслоенная формация. Итак, утверждение верно при
-расслоенная формация. Итак, утверждение верно при 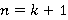 .
.
Из пунктов 1–3 по методу математической индукции утверждение верно для любого 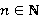 .
.
Из пунктов 1)–2) следует, что  — τ-замкнутая
— τ-замкнутая  -расслоенная формация. Лемма доказана.
-расслоенная формация. Лемма доказана.
Следствие 2.4.1. Пусть 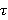 — подгрупповой функтор,
— подгрупповой функтор,  — FR-функция. Тогда пересечение любой совокупности τ-замкнутых n-кратно расслоенных формаций с направлением
— FR-функция. Тогда пересечение любой совокупности τ-замкнутых n-кратно расслоенных формаций с направлением  является τ-замкнутой n-кратно расслоенной формацией с направлением
является τ-замкнутой n-кратно расслоенной формацией с направлением  для любого
для любого 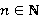 .
.
В работе [7] изучаются произведения Ω-расслоенных формаций. Следующий результат продолжает данные исследования.
Лемма 2.5. Пусть 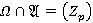 ,
, 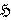 — Ω-расслоенная формация с bnr-направлением
— Ω-расслоенная формация с bnr-направлением  . Тогда формация
. Тогда формация 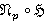 является Ω-расслоенной формацией с направлением
является Ω-расслоенной формацией с направлением  .
.
Доказательство. Согласно лемме 2.3, формация 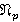 является Ω-расслоенной формацией с направлением
является Ω-расслоенной формацией с направлением  . Пусть
. Пусть 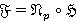 ,
, 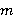 и
и 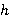 — внутренние Ω-спутникиформаций
— внутренние Ω-спутникиформаций 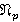 и
и 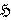 соответственно,
соответственно,  — ΩF-функция, такая что
— ΩF-функция, такая что 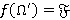 ,
, 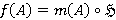 для всех
для всех 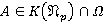 и
и 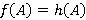 для всех
для всех 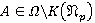 . Пусть
. Пусть 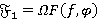 . Покажем, что
. Покажем, что 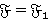 .
.
Так как  является r-направлением, то по лемме 1.3
является r-направлением, то по лемме 1.3 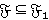 . Допустим, что
. Допустим, что 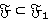 и
и 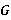 — группа наименьшего порядка из
— группа наименьшего порядка из 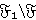 . Тогда
. Тогда 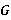 — монолитическая группа с монолитом
— монолитическая группа с монолитом 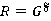 . Так как
. Так как 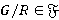 , то
, то 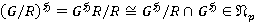 . Поскольку
. Поскольку 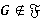 , то
, то 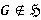 , и значит,
, и значит, 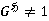 . Тогда
. Тогда 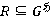 . Поэтому
. Поэтому 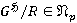 .
.
Пусть 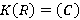 . Так как
. Так как 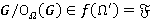 , то
, то 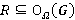 и
и 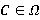 . Если
. Если 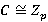 , то
, то 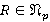 , и значит, ввиду
, и значит, ввиду 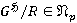 , имеем
, имеем 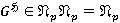 . Следовательно,
. Следовательно, 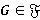 . Противоречие. Пусть
. Противоречие. Пусть 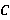 — неабелева группа. Так как
— неабелева группа. Так как  — n-направление, то
— n-направление, то 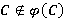 . Следовательно,
. Следовательно, 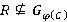 , и значит,
, и значит, 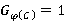 . Тогда
. Тогда 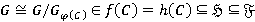 . Противоречие. Следовательно,
. Противоречие. Следовательно, 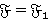 , и поэтому формация
, и поэтому формация 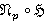 является Ω-расслоенной формацией с направлением
является Ω-расслоенной формацией с направлением  . Лемма доказана.
. Лемма доказана.
3. Спутники 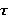 -замкнутых
-замкнутых 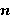 -кратно
-кратно 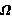 -расслоенных формаций
-расслоенных формаций
В следующей теореме устанавливается взаимосвязь между τ-замкнутостью 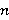 -кратно Ω-расслоенной формации с направлением
-кратно Ω-расслоенной формации с направлением  и τ-замкнутостью ее
и τ-замкнутостью ее  -спутника в случае, когда
-спутника в случае, когда 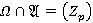 .
.
Теорема 3.1. Пусть 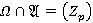 ,
,  — Ω-расслоенная формация с bnr-направлением
— Ω-расслоенная формация с bnr-направлением  ,
, 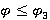 ,
, 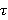 — регулярный Ωφ-радикальный подгрупповой функтор, замкнутый относительно композиционных факторов,
— регулярный Ωφ-радикальный подгрупповой функтор, замкнутый относительно композиционных факторов, 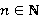 . Тогда формация
. Тогда формация  является τ-замкнутой
является τ-замкнутой  -расслоенной формацией в том и только том случае, когда
-расслоенной формацией в том и только том случае, когда  обладает хотя бы одним τ-замкнутым
обладает хотя бы одним τ-замкнутым  -спутником.
-спутником.
Доказательство. Необходимость. Пусть  —
— 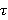 -замкнутая
-замкнутая  -расслоенная формация. Поскольку
-расслоенная формация. Поскольку  — br-направление и
— br-направление и 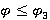 , то по лемме 1.7
, то по лемме 1.7  имеет единственный максимальный внутренний Ω-спутник
имеет единственный максимальный внутренний Ω-спутник 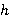 , причем
, причем 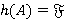 для всех
для всех 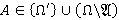 и
и 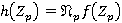 , где
, где  — произвольный внутренний Ω-спутник формации
— произвольный внутренний Ω-спутник формации  . Поэтому для любого
. Поэтому для любого 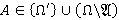 формация
формация 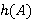 является τ-замкнутой, а согласно лемме 2.1 —
является τ-замкнутой, а согласно лемме 2.1 —  -расслоенной формацией.
-расслоенной формацией.
Покажем, что 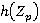 — τ-замкнутая
— τ-замкнутая  -расслоенная формация. Согласно доказательству леммы 2 [10],
-расслоенная формация. Согласно доказательству леммы 2 [10], 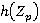 — τ-замкнутая формация. Покажем, что
— τ-замкнутая формация. Покажем, что 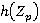 —
— -расслоенная формация. Так как
-расслоенная формация. Так как  —
—  -расслоенная формация, то
-расслоенная формация, то  обладает
обладает  -спутником
-спутником 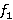 . Пусть
. Пусть 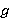 — ΩF-функция, такая, что
— ΩF-функция, такая, что 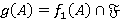 для всех
для всех 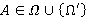 . Согласно лемме 1.4,
. Согласно лемме 1.4, 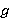 является Ω-спутником формации
является Ω-спутником формации  . Так как по лемме 2.1
. Так как по лемме 2.1  является
является  -расслоенной формацией, то по лемме 2.4
-расслоенной формацией, то по лемме 2.4 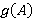 —
—  -расслоенная формация для любого
-расслоенная формация для любого 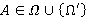 . Таким образом, Ω-спутник
. Таким образом, Ω-спутник 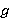 формации
формации  является
является  -спутником. Тогда, согласно леммам 1.6 и 2.5,
-спутником. Тогда, согласно леммам 1.6 и 2.5, 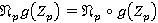 —
—  -расслоенная формация. Из строения
-расслоенная формация. Из строения 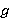 следует, что
следует, что 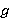 является внутренним Ω-спутником формации
является внутренним Ω-спутником формации  , и поэтому
, и поэтому 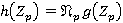 . Тем самым установлено, что
. Тем самым установлено, что 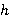 — τ-замкнутый
— τ-замкнутый  -спутник формации
-спутник формации  .
.
Достаточность. Пусть  — τ-замкнутый
— τ-замкнутый  -спутник формации
-спутник формации  ,
, 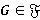 и
и 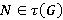 . Покажем, что
. Покажем, что 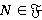 . Так как
. Так как 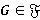 , то
, то 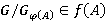 для любого
для любого 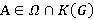 . Поскольку
. Поскольку 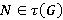 и
и 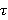 — подгрупповой функтор, замкнутый относительно композиционных факторов, то
— подгрупповой функтор, замкнутый относительно композиционных факторов, то 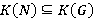 , и значит,
, и значит, 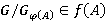 для любого
для любого 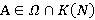 . Пусть
. Пусть 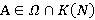 . Из
. Из 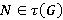 , ввиду регулярности подгруппового функтора
, ввиду регулярности подгруппового функтора 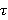 , получаем
, получаем 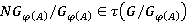 . Отсюда, в силу τ-замкнутости формации
. Отсюда, в силу τ-замкнутости формации 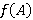 , следует, что
, следует, что 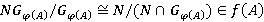 . Так как подгрупповой функтор
. Так как подгрупповой функтор 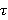 является φ-радикальным и
является φ-радикальным и 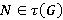 , то
, то 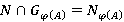 и
и 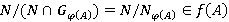 . Далее, из
. Далее, из 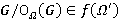 ,
, 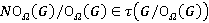 и τ-замкнутости формации
и τ-замкнутости формации 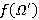 имеем
имеем 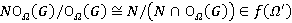 . Так как
. Так как 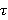 — Ω-радикальный подгрупповой функтор, то
— Ω-радикальный подгрупповой функтор, то 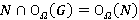 и
и 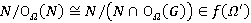 . Таким образом, по определению Ω-расслоенной формации,
. Таким образом, по определению Ω-расслоенной формации, 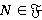 , и значит, формация
, и значит, формация  является τ-замкнутой. Согласно определению n-кратно Ω-расслоенной формации,
является τ-замкнутой. Согласно определению n-кратно Ω-расслоенной формации,  —
—  -расслоенная формация. Теорема доказана.
-расслоенная формация. Теорема доказана.
Обозначим через 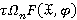 пересечение всех τ-замкнутых
пересечение всех τ-замкнутых  -расслоенных формаций, содержащих множество групп
-расслоенных формаций, содержащих множество групп 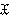 ;
; 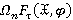 — пересечение всех
— пересечение всех  -расслоенных формаций, содержащих
-расслоенных формаций, содержащих 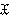 и обладающих хотя бы одним τ-замкнутым
и обладающих хотя бы одним τ-замкнутым  -спутником.
-спутником.
Следствие 3.1.1. Пусть 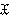 — непустой класс групп,
— непустой класс групп, 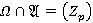 ,
,  — bnr-направление Ω-расслоенной формации,
— bnr-направление Ω-расслоенной формации, 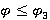 ,
, 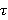 — регулярный
— регулярный 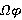 -радикальный подгрупповой функтор, замкнутый относительно композиционных факторов. Тогда
-радикальный подгрупповой функтор, замкнутый относительно композиционных факторов. Тогда 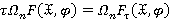 .
.
Теорема 3.2. Пусть 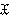 — непустой класс групп,
— непустой класс групп, 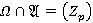 ,
,  — τ-замкнутая
— τ-замкнутая  -расслоенная формация с bnr-направлением
-расслоенная формация с bnr-направлением  ,
, 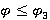 ,
, 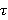 — регулярный Ωφ-радикальный подгрупповой функтор, замкнутый относительно композиционных факторов. Тогда
— регулярный Ωφ-радикальный подгрупповой функтор, замкнутый относительно композиционных факторов. Тогда 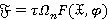 обладает единственным минимальным τ-замкнутым
обладает единственным минимальным τ-замкнутым  -спутником
-спутником  таким, что
таким, что 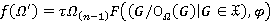 ,
, 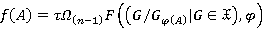 для всех
для всех 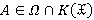 и
и 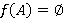 , если
, если 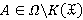 .
.
Доказательство. Так как множество 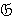 всех конечных групп является τ-замкнутой
всех конечных групп является τ-замкнутой  -расслоенной формацией и
-расслоенной формацией и 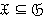 , то формация
, то формация 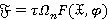 существует, и согласно следствию 3.1.1, множество
существует, и согласно следствию 3.1.1, множество 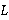 всех τ-замкнутых
всех τ-замкнутых  -спутников формации
-спутников формации  непусто. Пусть
непусто. Пусть 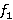 — пересечение всех элементов из
— пересечение всех элементов из 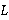 . Тогда
. Тогда 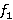 является Ω-спутником формации
является Ω-спутником формации  . По лемме 2.4 все значения
. По лемме 2.4 все значения 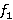 являются τ-замкнутыми
являются τ-замкнутыми  -расслоенными формациями. Следовательно,
-расслоенными формациями. Следовательно, 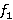 — единственный минимальный
— единственный минимальный  -спутник формации
-спутник формации  в силу своего строения.
в силу своего строения.
Пусть  — ΩF-функция, описанная в заключении теоремы. Покажем, что
— ΩF-функция, описанная в заключении теоремы. Покажем, что 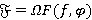 . Пусть
. Пусть 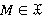 . Тогда
. Тогда 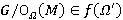 и
и 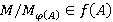 для всех
для всех 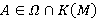 . Это означает, что
. Это означает, что 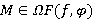 и
и 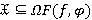 . Поскольку все значения
. Поскольку все значения  являются τ-замкнутыми
являются τ-замкнутыми  -расслоенными формациями, то формация
-расслоенными формациями, то формация 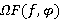 является
является  -расслоенной формацией и
-расслоенной формацией и 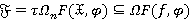 .
.
Покажем, что 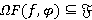 . Пусть
. Пусть 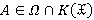 . Тогда найдется такая группа
. Тогда найдется такая группа 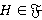 , что
, что 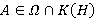 . Поэтому
. Поэтому 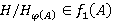 и
и 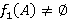 . Пусть
. Пусть 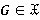 . Если
. Если 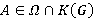 , то
, то 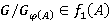 . Пусть
. Пусть 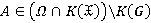 . Так как
. Так как  — r-направление, то
— r-направление, то 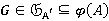 и
и 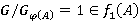 . Таким образом,
. Таким образом, 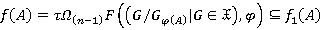 . Из
. Из 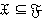 имеем
имеем 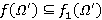 . Если
. Если 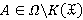 , то
, то 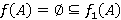 . Следовательно,
. Следовательно, 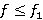 и
и 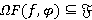 . Тем самым установлено, что
. Тем самым установлено, что 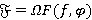 , и значит,
, и значит, 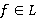 . Поскольку
. Поскольку 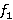 — единственный минимальный τ-замкнутый
— единственный минимальный τ-замкнутый  -спутник формации
-спутник формации  , то
, то 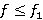 влечет
влечет 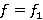 . Теорема доказана.
. Теорема доказана.
Замечание. В [11] получено описание единственного минимального τ-замкнутого  -спутника τ-замкнутой
-спутника τ-замкнутой  -расслоенной формации
-расслоенной формации  мультиоператорных
мультиоператорных 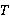 -групп в том случае, когда
-групп в том случае, когда  обладает по крайней мере одним τ-замкнутым
обладает по крайней мере одним τ-замкнутым  -спутником.
-спутником.
Введем обозначение:
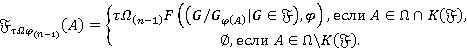
Теорема 3.3. Пусть 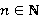 ,
, 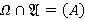 , где
, где 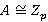 ,
,  — bnr-направление Ω-расслоенной формации,
— bnr-направление Ω-расслоенной формации, 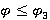 ,
, 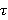 — регулярный Ωφ-радикальный подгрупповой функтор, замкнутый относительно композиционных факторов,
— регулярный Ωφ-радикальный подгрупповой функтор, замкнутый относительно композиционных факторов,  — τ-замкнутая
— τ-замкнутая  -расслоенная формация. Тогда
-расслоенная формация. Тогда 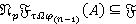 .
.
Доказательство. Пусть 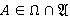 ,
, 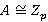 . Покажем, что
. Покажем, что 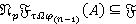 . Отметим, что для любой группы
. Отметим, что для любой группы 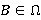 справедливо равенство:
справедливо равенство:
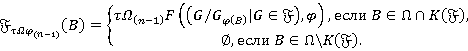
Если 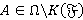 , то
, то 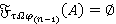 , и значит,
, и значит, 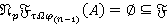 . Пусть
. Пусть 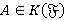 . Так как
. Так как 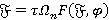 , то по теореме 3.2 формация
, то по теореме 3.2 формация  обладает единственным минимальным τ-замкнутым
обладает единственным минимальным τ-замкнутым 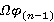 -спутником
-спутником  , причем для любого
, причем для любого 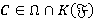 справедливо равенство
справедливо равенство 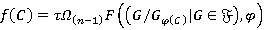 . Следовательно,
. Следовательно, 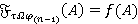 . Так как
. Так как  является
является 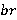 -направлением и
-направлением и  — внутренний
— внутренний 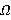 -спутник формации
-спутник формации  , то по лемме 1.5
, то по лемме 1.5 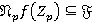 и, поскольку
и, поскольку 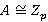 , получаем
, получаем 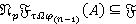 . Теорема доказана.
. Теорема доказана.
Следствие 3.3.1. Пусть 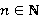 ,
, 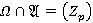 ,
,  — bnr-направление Ω-расслоенной формации,
— bnr-направление Ω-расслоенной формации, 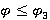 , τ — регулярный Ωφ-радикальный подгрупповой функтор, замкнутый относительно композиционных факторов,
, τ — регулярный Ωφ-радикальный подгрупповой функтор, замкнутый относительно композиционных факторов,  — τ-замкнутая
— τ-замкнутая  -расслоенная формация с внутренним
-расслоенная формация с внутренним  -спутником
-спутником  . Тогда
. Тогда 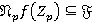 .
.
Литература:
1. Gaschütz W. Zur Theorie der endlichen auflösbaren Gruppen. — Math. Z., 1963. Vol. 80, № 4. — S. 300–305.
2. Шеметков Л. А. Формации конечных групп. — М.: Наука, 1978. — 272 с.
3. Скиба А. Н. Алгебра формаций. — Минск: Беларуская навука, 1997. — 240 с.
4. Ведерников В. А., Сорокина М. М. Ω-расслоенные формации и классы Фиттинга конечных групп // Дискретная математика. Т.13. Вып. 3, 2001. — С. 125–144.
5. Каморников С. Ф., Селькин М. В. Подгрупповые функторы и классы конечных групп. — Минск: Беларуская навука, 2003. — 254 с.
6. Скиба А. Н., Шеметков Л. А. О минимальном композиционном экране композиционной формации // Вопросы алгебры. Вып. 7, 1992. — С. 39–43.
7. Vedernikov V. A. Maximal satellites of Ω-foliated formations and Fitting classes // Proc. Steklov Inst. Math. № 2, 2001. — P. 217–233.
8. Ведерников В. А., Демина Е. Н. Ω-расслоенные формации мультиоператорных Т-групп // Сиб. матем. ж., 2010. Т. 51. № 5. — С. 990–1009.
9. Монахов В. С. Введение в теорию конечных групп и их классов. — Минск: Вышэйшая школа, 2006. — 207 с.
10. Корпачева М. А., Сорокина М. М. Критические Ω-расслоенные τ-замкнутые формации конечных групп // Вестник Брянского государственного университета. № 4: Точные и естественные науки. Выпуск 2. — Брянск: РИО БГУ, 2012. — С. 75‒79.
11. Demina E. N. Ω1-foliated τ-closed formations of T-groups // 8th International Algebraic Conference in Ukraine: book of abstracts. — Luhansk: LTSNU, 2011. — P. 97.







