Сложные тестовые композиции матричного типа в совокупности с их логистическими связями, представляющие собой фактически систему распознавания образов с заданным числом событий и им соответствующих признаков (рис. 1), могут выступать как аналоги нейронных сетей.
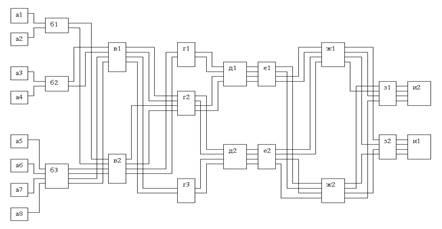
Рис. 1. Логистическая модель сложной тестовой композиции матричного типа (8 событий (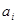
), 8 множеств признаков (
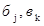и т. д.))
Нейронная сеть — это сеть с конечным числом слоев из однотипных элементов — аналогов нейронов с различными типами связей между слоями. При этом число нейронов в слоях выбирается исходя из необходимости обеспечения заданного качества решения задачи, а число слоев нейронов — как можно меньшее для сокращения времени решения задачи. Таким образом, в качестве слоев могут выступать множества композиции (множества А, Б, В, Г, Д и т. д.), а аналоги нейронов — однотипные элементы множеств (элементы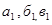 
и т. д.).
Рассмотрим аналогию между структурами логистических моделей тестов и искусственным нейроном. Нейрон обладает группой синапсов — однонаправленных входных связей, соединенных с выходами других нейронов, а также имеет аксон — выходную связь данного нейрона, с которой сигнал поступает на синапсы следующих нейронов (рис.2).
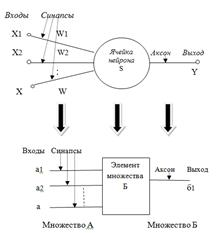
Рис. 2 Аналогия структуры искусственного нейрона и элемента логистической модели
В состав логистической структуры входят элементы множеств, которые также имеют входные связи, так называемые синапсы, от соответствующих им элементов основного и вспомогательных множеств [2], а также выходную связь — аксон, которая направлена к соответствующему элементу, в рамках системы распознавания образов, для которого уже является входной связью — синапсом.
При воссоздании всех связей цепочки решается задача тестовой композиции о распознавании образов путем поэтапного соединения элементов — нейронов посредством входных и выходных связей, синапсов и аксонов.
Свойство нейрона описывается уровнем активации нейрона, т. е. каждый вход умножается на соответствующий вес, аналогичный синаптической силе, и все произведения суммируются. Суммирующий блок (1) соответствует телу биологического элемента.
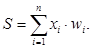(1)
Свойство элемента множества логистической модели, с точки зрения нейронных сетей, может быть описано умножением каждого входа на вероятность распознавания образа P (вес) с помощью соответствующего данному входу элемента, аналогичный синаптической силе элемента. При этом суммирующий блок (2) соответствует образу (телу) распознаваемого объекта:
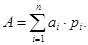(2)
Выход нейрона является функцией его состояния, где F — активационная функция:
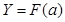, (3)
Функция активации может быть как гомогенной (однородной), то есть одна и та же для всех нейронов сети (множеств композиции), так и гетерогенной, неоднородной, то есть зависит от нескольких параметров, значения которых меняются от нейрона (множества) к нейрону (множеству), что соответствует различным формам представления тестовых композиций, а следственно, на их базе и логистических структур.
Активационная функция с насыщением, так называемая логистическая функция или сигмоид (рис.3), определяет функцию состояния логистической модели тестовой композиции (4) и выглядит следующем образом:
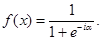(4)
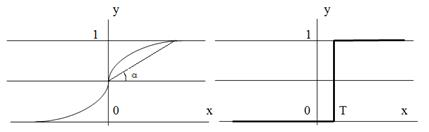
а) б)
Рис. 3. Активационные функции: а) сигмоид; б) функция единичного скачка
При уменьшении α сигмоид становится более пологим, в пределе при α = 0 вырождаясь в горизонтальную линию на уровне 0,5. При увеличении α сигмоид приближается по внешнему виду к функции единичного скачка с порогом Т в точке x = 0. Из выражения для сигмоида очевидно, что выходное значение нейрона лежит в диапазоне [0,1], что соответствует дихотомической шкале в тестовых технологиях (рис.3).
Система распознавания образов представляет собой цепочку поэтапного логического присоединения элементов (характеристик, свойств) объекта исследования для его идентификации. Нейронные сети с пороговой функцией (функции активации) дихотомического типа (тип «да» — «нет» или «1» — «0») в решении задачи распознавания могут выступать в роли математического аппарата, а именно, в роли «кодировщика» в допустимом диапазоне соответствующей характеристики объекта исследования. Если значение элемента попадает в допустимый интервал, то результатом будет логическая «1», иначе — логический «0». Данный процесс осуществляется с помощью функции активации дихотомического типа, поэтапно продвигаясь к последующим характеристикам.
Рассмотрим вышеописанное на примере тестового задания матричного типа «Классификация катодов», где в качестве признаков (характеристик) катодов выступают рабочая температура, удельная эмиссия, удельная мощность, эффективность и долговечность (рис. 4).
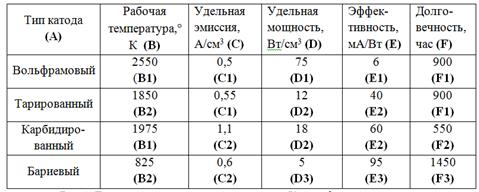
Рис. 4. Тестовое задание матричного типа «Классификация катодов»
Матричная структура включает основное множество (A), элементы которого необходимо распознать, и вспомогательные множества(B,C,D,E,F), описывающие свойства и характеристики элементов основного множества (A).
Таким образом, для идентификации объектов исследования основного множества необходимо воссоздать логические цепочки путем последовательного присоединения элементов вспомогательных множеств (Рис.5).
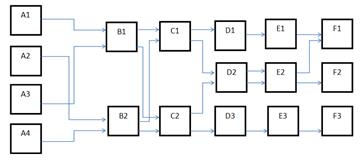
Рис. 5. Логистическая модель тестового задания матричного типа «Классификация катодов»
Логистическая модель тестового задания определяется такими понятиями как достаточность и избыточность признаков. Таким образом, достаточными признаками называются такие признаки, при наличии (выполнении, соблюдении) которых утверждение является истинным и полностью идентифицирует объект исследования основного множества А. Избыточными признаками называются такие признаки, при наличии (выполнении, соблюдении) которых утверждение является чрезмерно истинным, которое в свою очередь направленно на повышение информативности системы.
В тестовом задание матричного типа «Классификация катодов» с точки зрения достаточности и избыточности признаков необходимым является наличие 2 и более множеств в зависимости от информативности совокупности элементов для идентификации объектов исследования.
Используя нейронные сети с пороговой функцией дихотомического типа, на каждом этапе распознавания, проводится «кодировка» при каждом переходе к последующему вспомогательному множеству, что позволит при анализе результатов тестирования выявить те этапы, на котором произошла ошибка.
Таким образом, для тестового задания «Классификация катодов» интервалы кодирования сигнала выглядит следующим образом (табл.1):
Таблица 1
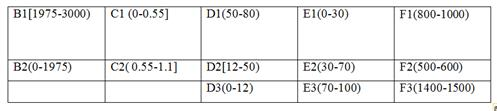
Пример результата выполнения тестового задания матричного типа логистической структуры как системы распознавания образов приведена на рис. 6
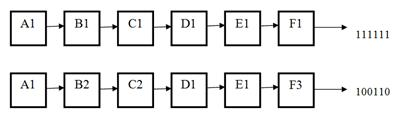
Рис. 6. Результат распознавания основного множества А тестового задания «Классификация катодов»
Приведенное описание основных элементов логистической модели тестовых структур как аналога нейронной сети, представляет интерес для теории и практики.
Литература:
1. Ткаченко И. М., Захаров А. А., Кожанова Е. Р. Исследование эффекта прецессии спиновой структуры как элемента системы распознавания с использованием аппарата нейронных сетей // Theoretical & Applied Science. 2014. № 2 (10). С. 40–43.
2. Ткаченко И. М., Захаров А. А., Кожанова Е. Р. Персептрон как структурный элемент системы распознавания образов // Актуальные проблемы современной науки: сборник статей Международной научно-практической конференции: в 4 ч. отв. ред. А. А. Сукиасян. Уфа: РИЦ БашГУ, 2013. Т.4. С. 248–251.
3. Ткаченко И. М., Захаров, Калашникова Е. Н. Проектирование моделей тестовых структур на основе логистических схем с произвольным числом множеств и элементов // Вестник Саратовского государственного технического университета, 2009. № 2 (39) Вып.2. С.92–101.
