Представлена физическая модель гидроимульсных механизмов бурильных машин с одним и двумя колебательными контурами. Получены дифференциальные уравнения, описывающие механические и гидравлические процессы, протекающие в механизме за весь цикл его работы. Представлено сравнение моделей гидроимульсного механизма бурильных машин. Аналитическое решение, позволяет сделать вывод об эффективности применения таких механизмов.
Ключевые слова: гидроимпульсный механизм, гидропульсатор, безбойковый механизм, вынужденные колебания, собственная частота, резонанс.
Прогрессивным направлением в развитии машин и механизмов ударного действия является создание силовых импульсных систем с гидравлическим приводом [1]. Исследования вращательного бурения режущим инструментом с наложением на него высокоэнергетических упругих колебаний показали возможность в 2–2,5 раза интенсифицировать процесс разрушения горных пород, в 1,5–2 раза повысить износостойкость режущего инструмента, на 2–3 категории крепости пород по шкале проф. М. М. Протодьяконова расширить область эффективного применения вращательного бурения скважин при повышении производительности труда на 40–70 % [2].
В работах [3–9] рассмотрена оригинальная модель гидроимпульсного силового механизма бурильных машин, в которых силовые импульсы возникают за счет резонансных колебаний гидроцилиндра с реактивной массой. Возникает вопрос об эффективности данного оригинального механизма и сравнения его с упрощенным механизмом без колебательного контура, в котором силовые импульсы формируются только плунжерным гидропульсатором.
Рассмотрим модель гидроимпульсного силового механизма без колебательного контура (рис. 1). Импульсы давления жидкости формируются следующим образом. При работе гидропульсатора, плунжер совершает возвратно-поступательное движение, при этом создаются импульсы давления жидкости, которые через поршень и буровую штангу передаются на обрабатываемую среду.
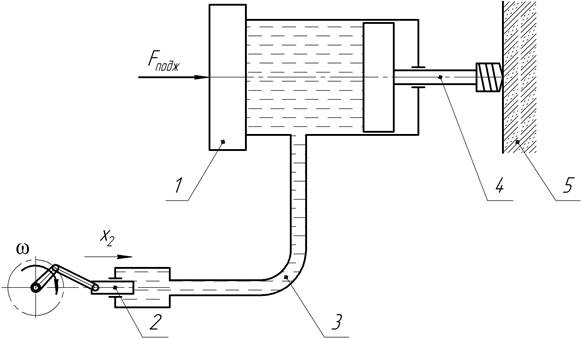
Рис. 1. Модель гидроимульсного механизма без колебательного контура: 1 — гидроцилинд; 2 — плунжер (пульсатор); 3 — рукав высокого давления (РВД); 4 — бурильный инструмент; 5 — разрушаемая порода
Вводим обобщенную координату: x2 — координата перемещения плунжера (рис. 1).
Уравнение расходов для системы будет:
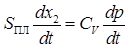 ,
,
здесь 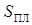 – площадь плунжера,
– площадь плунжера, 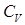 — коэффициент упругости гидросистемы, определяющий расход на деформацию элементов гидросистемы и сжимаемость жидкости.
— коэффициент упругости гидросистемы, определяющий расход на деформацию элементов гидросистемы и сжимаемость жидкости.
Преобразуем:
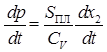
Проинтегрировав выражение, получаем
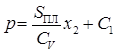 , (1)
, (1)
где С1 — постоянная интегрирования.
Подставляем начальные условия 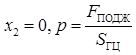 в (1), находим постоянную интегрирования
в (1), находим постоянную интегрирования
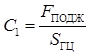 .
.
Плунжер движется по закону  , где r — радиус кривошипа привода плунжера. Подставляем закон движения плунжера и постоянную интегрирования в выражение (1), получаем уравнение колебаний давления в гидросистеме (усилия на бурильном инструменте):
, где r — радиус кривошипа привода плунжера. Подставляем закон движения плунжера и постоянную интегрирования в выражение (1), получаем уравнение колебаний давления в гидросистеме (усилия на бурильном инструменте):
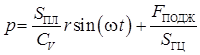 . (2)
. (2)
Из выражения можно найти амплитуду колебаний давления и максимальное значения давления в гидросистеме:
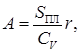
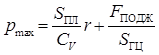 .
.
Рассмотрим модель гидроимпульсного силового механизма c двумя колебательными контуром и реактивной массой (рис. 2). Импульсы давления жидкости формируются следующим образом. При работе гидропульсатора, плунжер совершает возвратно-поступательное движение, при этом создаются импульсы давления жидкости, которые передаются в гидроцилиндр.
Так как гидроцилиндр поджат упругой силой, происходит его раскачка вместе с инерционной массой m. При этом происходит периодическое преобразование кинетической энергии массы m в потенциальную энергию деформированной системы жидкости и рукава — повышению давления в системе и обратно. При режиме работы системы близкого к резонансному, возникают импульсы давления значительной величины, которые через поршень и буровую штангу передаются на обрабатываемую среду.
Для вывода уравнений, описывающих данную систему, полагаем, что между двумя следующими друг за другом силовыми импульсами, гидроцилиндр неподвижен. Вводим следующие обобщенные координаты: x1 — координата перемещения корпуса гидроцилиндра; x2 — координата перемещения плунжера (рис. 2).
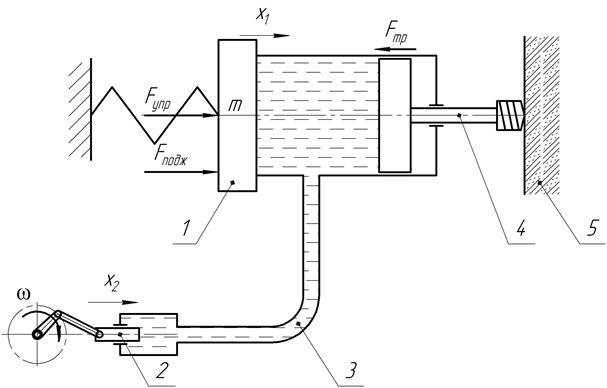
Рис. 2. Модель гидроимульсного механизма: 1 — гидроцилиндр с активной массой; 2 — плунжер; 3 — рукав высокого давления (РВД); 4 — бурильный инструмент; 5 — разрушаемая порода
Учитывая принятые допущения, дифференциальное уравнение движения гидроцилиндра можно представить в виде:
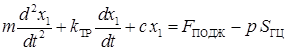 , (3)
, (3)
где m — масса, прикрепленная к корпусу гидроцилиндра; 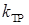 – коэффициент трения между поршнем и гидроцилиндром; с — жесткость пружины; p — давление в гидроцилиндре;
– коэффициент трения между поршнем и гидроцилиндром; с — жесткость пружины; p — давление в гидроцилиндре; 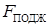 – постоянное усилие поджима;
– постоянное усилие поджима; 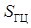 – площадь поршня гидроцилиндра.
– площадь поршня гидроцилиндра.
Уравнение расходов:
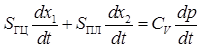 , (4)
, (4)
где 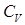 — коэффициент упругости гидросистемы, определяющий расход на деформацию элементов гидросистемы и сжимаемость жидкости.
— коэффициент упругости гидросистемы, определяющий расход на деформацию элементов гидросистемы и сжимаемость жидкости.
выражение (4) получили
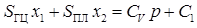 , (5)
, (5)
где С1 — постоянная интегрирования.
Подставляем начальные условия 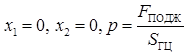 в (5), находим постоянную интегрирования
в (5), находим постоянную интегрирования
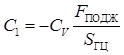 .
.
Из выражения (5) находим
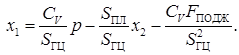 (6)
(6)
Подставляем закон движения плунжера в выражение (6) и дважды дифференцируем:
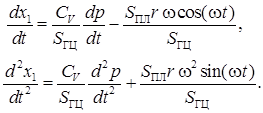
Подставляем в (3), получаем
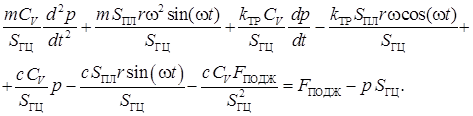
Преобразуем выражение к виду
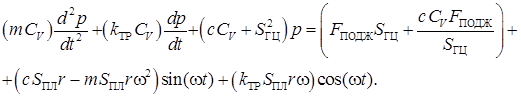 (7)
(7)
Вводим обозначения
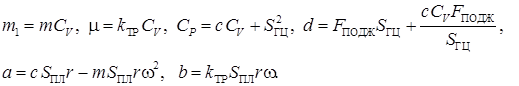
Тогда выражение (7) приобретает вид
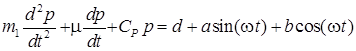
или
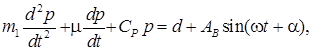 (8)
(8)
где 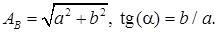
Делим (8) на 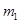 и получаем дифференциальное уравнение вынужденных колебаний с вязким сопротивлением [1]. Обозначим:
и получаем дифференциальное уравнение вынужденных колебаний с вязким сопротивлением [1]. Обозначим:
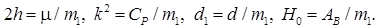
После подстановки в (6) получаем
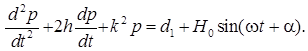 (9)
(9)
Решением уравнения (9) будет:

где
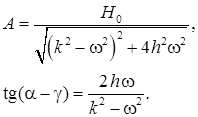
Или
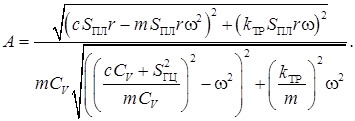
Из полученного решения можно найти требуемую частоту приводного двигателя плунжера, при которой система находится в резонансе, и амплитуда скачка давления максимальна:
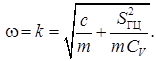
Максимальная амплитуда при этом будет:
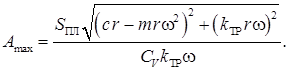
После преобразований получим:
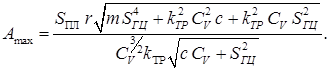
Параметры системы были равны:
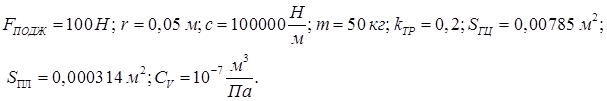
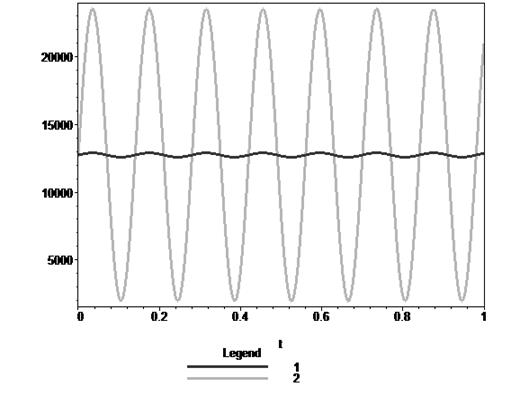
Рис. 3. Импульсы давления на поршне в резонансном режиме: 1 — гидроимпульсный механизм с одним колебательным контуром; 2 — гидроимпульсный механизм с двумя колебательными контурами
На рис. 3 представлено сравнение импульсов давления создаваемых гидроимпульсными механизмами с одним и двумя колебательными контурами при одних и тех же значениях параметров системы. Из рисунка видно значительное преимущество гидроимульсного механизма с двумя колебательным контуроми, т. к. амплитуда импульсов создаваемого им давления в резонансном режиме многократно больше, чем у гидроимпульсного механизма одним колебательным контуром.
Выводы:
По результатам математических исследований можно сделать вывод о том, что при одних и тех же исходных данных, колебания давления на поршне, а соответственно и силы на ударном инструменте выше в случае гидроимпульсного механизма с колеблющейся массой. Так же считая амплитуду давления одноконтурного механизма базовой можно оценить эффективность гидроимпульсного механизма.
Литература:
1. Бутенин Н. В., Лунц Я. Л., Меркин Д. Р. Курс теоретической механики: Учебник. В 2-х томах. Т. II.: Динамика. — 2-е изд. Перераб. и доп. — М.: Наука. Главная редакция физико-математической литературы, 1979. — 544 стр.
2. Липин А. А., Танайно А. С., Тимонин В. В. Современные погружные машины для бурения скважи. Горная техника: Каталог-справочник. — СПб.: ООО «Славутич», 2006. — С. 116–123.
3. Патент на ПМ 79924 РФ. МПК7 Е21В 6/02, B25D 16/00. Гидроимпульсная сваебойная машина / Пашков Е. Н., Зиякаев Г. Р., Юровский П. Г., Пономарев А. В. Опубл. 10.10.2013 г.
4. Патент на ПМ 71369 РФ. МПК7 Е21В 6/02, B25D 16/00. Станок для бурения скважин в подземных условиях / А. В. Шадрина, А. А. Казанцев, А. Л. Саруев, Л. А. Саруев. Опубл. 10.03.2008 г.
5. Шадрина А. В., Саруев Л. А., Саруев А. Л. Динамические процессы в колонне труб при вращательно-ударном бурении скважин малого диаметра из подземных горных выработок // Томск. Изд-во Томского политехнического университета. 2009.- 175 с.
6. Пашков Е. Н., Саруев Л. А., Зиякаев Г. Р. Математическое моделирование гидроимпульсного механизма бурильных машин // Горный информационно-аналитический бюллетень. — 2011. — № 5 — С. 26–31.
7. Пашков Е. Н., Зиякаев Г. Р., Кузнецов И. В. Дифференциальные уравнения процессов гидроимпульсного силового механизма бурильных машин / Пашков Е. Н., Зиякаев Г. Р., Кузнецов И. В. // Приволжский научный вестник. — 2013. — № 4 (20). — С. 32–36.
8. Пашков Е. Н., Зиякаев Г. Р., Юровский П. Г. Одноконтурный гидроимпульсный механизм бурильных машин // Горный информационно-аналитический бюллетень (научно-технический журнал). — 2013. — № 12. Отдельные статьи (специальный выпуск). Актуальные проблемы машиностроения. — С. 95–99.







