Наиболее простым инженерным способом аппроксимации корреляционных функций, позволяющим найти приближенное аналитическое выражение спектральной плотности, является метод треугольных корреляционных функций. Здесь корреляционная функция представляется в виде кусочно-линейной функции (алгебраическая сумма типовых треугольных корреляционных функций; при 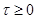 имеют вид, приводимый на рис.1).
имеют вид, приводимый на рис.1).
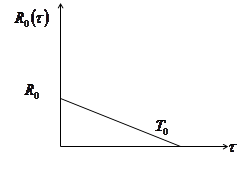
Рис.1. Треугольная корреляционная функция
Каждая типовая корреляционная функций определяется двумя параметрами — 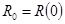 и
и 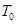 . Непосредственно из рисунка следует:
. Непосредственно из рисунка следует:

Отметим,  . Каждой типовой треугольной корреляционной функции
. Каждой типовой треугольной корреляционной функции 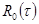 соответствует спектральная плотность
соответствует спектральная плотность
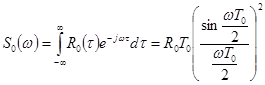 .
.
Введя 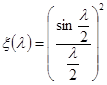 , получим
, получим 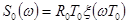 ; график функции
; график функции  на рис.2.
на рис.2.

Рис. 2. Вид 
Если 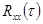 с достаточной степенью точности аппроксимируется алгебраической суммой
с достаточной степенью точности аппроксимируется алгебраической суммой 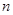 типовых треугольных корреляционных функций
типовых треугольных корреляционных функций 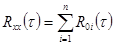 , то:
, то:
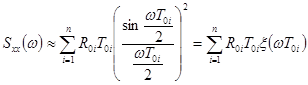 .
.
Точность определения спектральной плотности тем выше, чем меньше расхождение между корреляционными функциями: действительной и результирующей аппроксимированной. При этом несоответствие в значениях функции для малых 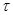 будет преимущественно вызывать отклонение в значениях спектральной плотности для больших
будет преимущественно вызывать отклонение в значениях спектральной плотности для больших  .
.
Взаимная спектральная плотность 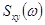 в общем случае является комплексной величиной:
в общем случае является комплексной величиной:
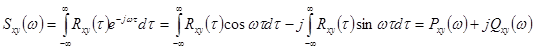 ;
;
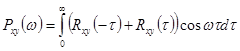 ,
, 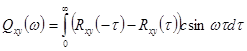
(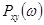 - четная функция, а
- четная функция, а 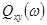 — нечетная).
— нечетная).
Введя 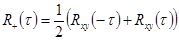 ,
, 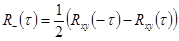
(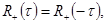
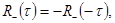
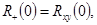

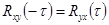 ),
),
получим
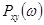 =
=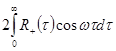 ,
, 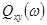 =
=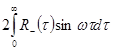 . (1)
. (1)
В силу четности 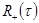 ее можно рассматривать как некоторую корреляционную функцию. Сравнивая далее выражение (1) для
ее можно рассматривать как некоторую корреляционную функцию. Сравнивая далее выражение (1) для 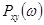 с формулой
с формулой
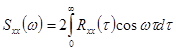 ,
,
видим, что они по форме совпадают. Следовательно, для вычисления 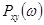 по
по 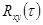 можно воспользоваться одним из методов приближенного вычисления спектральной плотности, которые рассмотрели ранее.
можно воспользоваться одним из методов приближенного вычисления спектральной плотности, которые рассмотрели ранее.
Рассмотрим методы приближенного вычисления мнимой части взаимной спектральной плотности (аппроксимация корреляционной функции 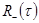 типовыми корреляционными функциями): метод типовых треугольных и метод типовых экспоненциальных корреляционных функций.
типовыми корреляционными функциями): метод типовых треугольных и метод типовых экспоненциальных корреляционных функций.
Сначала рассмотрим метод типовых треугольных корреляционных функций. Наиболее удобно и просто 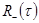 аппроксимировать кусочно-линейной функцией. Тогда в качестве типовых корреляционных функций могут быть взяты треугольные корреляционные функции. При этом функция
аппроксимировать кусочно-линейной функцией. Тогда в качестве типовых корреляционных функций могут быть взяты треугольные корреляционные функции. При этом функция 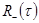 приближенно представляется в виде алгебраической суммы какого-либо числа типовых треугольных корреляционных функций. Мнимая часть
приближенно представляется в виде алгебраической суммы какого-либо числа типовых треугольных корреляционных функций. Мнимая часть 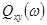 взаимной спектральной плотности будет также приближенно представляться в виде алгебраической суммы функций от
взаимной спектральной плотности будет также приближенно представляться в виде алгебраической суммы функций от  , соответствующих типовым треугольным функциям.
, соответствующих типовым треугольным функциям.
Если, как и ранее типовую треугольную функцию обозначить 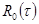 , то:
, то:
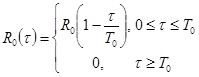
введя функцию 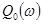 , определяемую формулой, аналогичной (1), получим:
, определяемую формулой, аналогичной (1), получим:
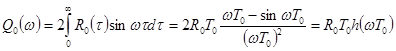 ,
, 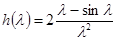 (рис.3).
(рис.3).
Если 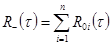 , то
, то  .
.
Метод экспоненциальных корреляционных функций аналогичен методу типовых экспоненциальных корреляционных функций, использованному для аппроксимации корреляционных функций. Для положительных 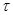 функция
функция 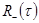 представляется в виде суммы типовых экспоненциальных корреляционных функций
представляется в виде суммы типовых экспоненциальных корреляционных функций
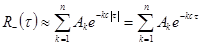 ,
,
где 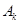 — некоторые коэффициенты,
— некоторые коэффициенты, 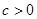 ;
; 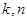 — целые числа.
— целые числа.
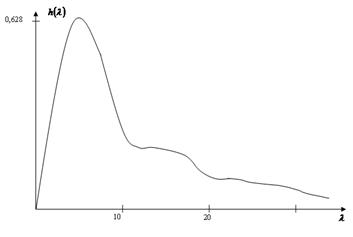
Рис.3. Вид 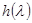
Заметим, что, так как 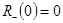 , то
, то 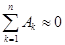 . Все формулы, полученные ранее для вычисления
. Все формулы, полученные ранее для вычисления 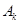 , остаются в силе. Получим:
, остаются в силе. Получим:
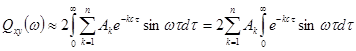 ;
; 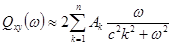 .
.
В силу того, что полученная таким образом 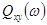 есть нечетная функция, то эта формула пригодна для вычисления
есть нечетная функция, то эта формула пригодна для вычисления 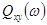 при
при 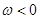 .
.
Приведенные методы эффективно использовались при составлении когнитивной карты формирования управляющих воздействий оператора в зависимости от параметров объекта управления [1…3].
Литература:
1. E. Budylina, A. Danilov, I. Garkina. Control of multiobjective complex systems / Contemporary Engineering Sciences, Vol. 8, 2015, no. 10, 441–445. http://dx.doi.org/10.12988/ces.2015.5276.
2. Гарькина И.А, Данилов А. М., Пылайкин С. А. Транспортные эргатические системы: информационные модели и управление / Мир транспорта и технологических машин. — № 1(40). — 2013. — С.115–122.
3. Данилов А. М., Гарькина И. А., Гарькин И. Н. Спектральные методы при анализе динамических систем // Региональная архитектура и строительство. — 2014. — № 3. — С. 109–113.







