Создание тонких пленок – это одна из важных составляющих в машиностроении, в частности в электронике. На основе тонких пленок создают тонкопленочные резисторы и другие пассивные элементы, которые находятся в цепи постоянного или переменного тока. К тому же, с помощью тонких пленок можно модифицировать поверхность материала в сторону улучшения физических, химических, биологических характеристик и.т.д.
Данная работа раскрывает проблемы создания равномерных тонких пленок при магнетронном распылении. Исследование описывает программу, разработанную в среде MATLAB, которая моделирует процесс осаждения на подложке сложной формы, в частности параболоида. При этом процесс осаждения моделируется при одном магнетроне. Программа при расчете моделирует процесс осаждения на параболоид, при этом расстояние до магнетрона и форму параболоида можно регулировать.
Одной из основных характеристик тонкой пленки является ее равномерность.[1] Создание равномерных тонких пленок является не простой задачей, так как материал, на котором необходимо создать тонкую пленку, может быть любой формы, к тому же, из-за пространственной неравномерности потоков распыленных частиц, пленки, в основном, получаются неравномерные.
Было решено создать такую систему, которая бы моделировала процесс осаждения при любом материале мишени, создавала равномерную толщину пленки и сама считала, сколько магнетронов при этом понадобится. Для создания таких тонких пленок была создана программа. Данная программа моделирует нанесение тонкой пленки на параболоид любой формы, в случае одного магнетрона. Моделируется процесс нанесения пленки при движении параболоида вокруг своей оси, и без движения параболоида. Естественно, в данном случае пленка не получится равномерной, но над этим работа продолжается.
Такая программа поможет предприятиям автоматизировать процесс нанесения пленки в магнетронно-распылительных системах. Что увеличит производительность труда рабочих и инженеров, которые непосредственно меняют положение магнетрона для получения равномерной тонкой пленки.
При моделировании были приняты следующие допущения:
1.Распылённые атомы летят прямолинейно и конденсируются в точке соударения с подложкой.
2. Положение между анодом и катодом, не влияет на распределение плазмы в камере.
3. Распределение скорости распыления была получена путем измерения глубины эрозионной канавки до и после распыления.
4.Функция распыление одинакова по всей площади мишени.
5.Функция распределения толщины пленки идентична функции косинуса.
В основе расчета лежит формула
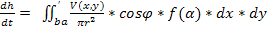 (1)
(1)
где h – толщина пленки, t – время, a,b – координаты на мишени, r – расстояние от расчетной точки до элементарной площадки на мишени, 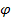 – угол падения атомов на подложку,
– угол падения атомов на подложку, 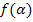 – функция распыления, V(x,y) – распределение скорости распыления, r – кратчайшее расстояние между подложкой и эрозионной канавкой в точках интегрирования.
– функция распыления, V(x,y) – распределение скорости распыления, r – кратчайшее расстояние между подложкой и эрозионной канавкой в точках интегрирования.
Так как программа позволяет моделировать процесс осаждения при любом веществе мишени, то функция распыления атомов может иметь различные значения в зависимости от вещества, которое осаждается на подложку. В настоящее время, в целях экономии времени, угловые распределения распыленных атомов приблизительно считались равными одному косинусному члену. Поэтому функция распыления атомов приравнивалась единице. Больше информации на тему распределения толщины пленки относительно осаждаемого металла можно найти в статье [2].
Скорость распыления определялась опытным путём, посредством измерения глубины эрозионной канавки по всей площади мишени.
Вначале расчета генерируется облако точек лежащих на поверхности подложки. Оно может создаваться по аналитической формуле, либо импортироваться из внешнего файла. После этого задаётся конфигурация магнетронов: распределение скоростей распыления мишеней, пространственное положение и движение относительно подложки. Затем происходит численное интегрирование согласно формуле (1).
Программа создана в среде Matlab, она позволяет рассчитывать толщину осаждаемой пленки, моделировать процесс осаждения в случае одного магнетрона на параболоиде.
Параболоид можно располагать относительно магнетрона на любое расстояние от него, геометрические характеристики параболоида (диаметр, глубина) также можно изменять. Данные действия можно регулировать в графе [параболоид] (Рисунок 1).
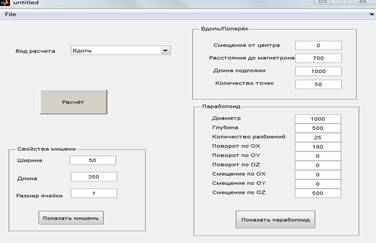
Рис. 1 – Интерфейс программы
Пример построения параболоида с диаметром – 1000 и глубиной – 500, можно увидеть на рисунке 2.
Мишень может быть любых размеров и формы, её форма и размер регулируются в графе [свойства мишени] (Рисунок 1). Пример построения мишени с шириной – 50 и длиной– 50, можно увидеть на рисунке 3.
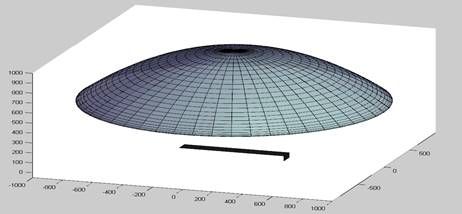
Рис. 2 – Пример построения параболоида, под параболоидом находится магнетрон, который расположен от параболоида на 500 условных единиц
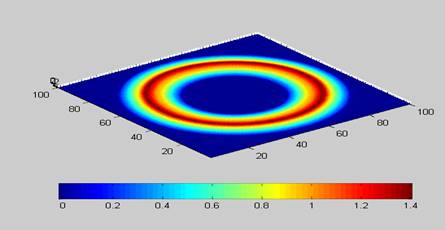
Рис. 3 – Пример построения мишени
При нажатии на кнопку [Расчет] программа моделирует распределение толщины при движимом или неподвижном магнетроне. Примеры вычисления распределения толщины на параболоиде при неподвижном магнетроне относительно подложки, приведены на рисунке 4. На подвижном магнетроне - на рисунке 5.
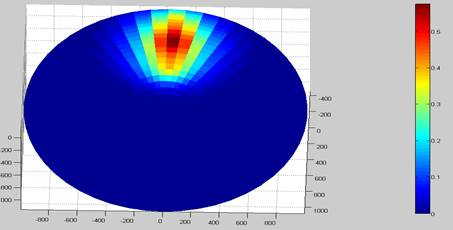
Рисунок 4 – Распределение толщины при неподвижном магнетроне.
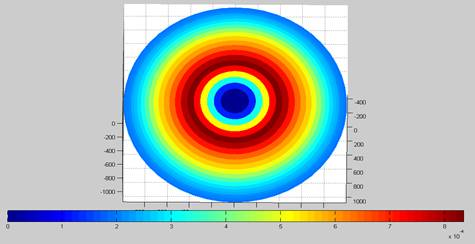
Рис. 5. Распределение толщины пленки при подвижном магнетроне.
Цветом обозначена толщина плёнки в относительных единицах
Литература:
1. Григорьев Ф.И. Осаждение тонких пленок и низкотемпературной плазмы и ионных пучков в технологии микроэлектроники. – Изд-во МГУ, 2006 – с. 22.
2. Мартыненко Ю.В., Шульга А.В., Шульга В.И. Угловое распределение атомов при магнетронном распылении поликристаллических мишеней – Журнал технической физики 2012, том 82, вып. 4 – с.6.







