Выполнен анализ распределения поперечной составляющей магнитного поля МПФС ЛБВ. Используется математический аппарат дискретного преобразования Фурье. Методика позволяет улучшить качество контроля магнитного поля постоянных магнитов МПФС. Расчеты выполнены для серии экспериментальных данных.
Ключевые слова: магнитное поле, магнитная периодическая фокусирующая система, лампа бегущей волны, дискретное преобразования Фурье.
This article describe the analysis of the transverse component of the magnetic field MPFS TWT with the involvement of the mathematical apparatus of the discrete Fourier transform. The technique allows to improve the quality control of the magnetic field of permanent magnets MPFS. The calculations were performed for a series of experimental data.
Keywords:Magnetic field, magnetic periodic focusing system, a traveling wave tube, a discrete Fourier transform.
В лампах бегущей волны (ЛБВ) малой и средней мощности в качестве узла, обеспечивающего фокусировку электронного потока, применяется магнитная периодическая фокусирующая система (МПФС), которая формируется из набора магнитов с противоположным направлением вектора магнитной индукции. Контроль технологических параметров МПФС, выполняемый на этапе сборки системы, является важной технологической процедурой. В процессе набора магнитов МПФС отбраковывают те, продольная или поперечная компонента которых не соответствует установленному диапазону допустимых значений [1]. До настоящего времени для контроля структуры магнитного поля МПФС на предприятиях применяют устаревшую измерительную аппаратуру, в которой измеряемый аналоговый сигнал выводится на самописец. Подобного рода оборудование не позволяет полноценно оценить структуру магнитного поля фокусирующей системы, поскольку выполнение многократных измерений связано с большими временными затратами, анализ же данных выполняется как правило ручным способом после окончания цикла измерения.
В качестве варианта решения описанной проблемы нами предлагается цифровая измерительная установка контроля магнитного поля МПФС. Установка позволяет выполнять измерения продольной или поперечной компонент магнитного поля заданное число раз в автоматическом режиме. В процессе измерений данные принимаются в цифровом виде и могут быть обработаны с привлечением ПК. Установка позволяет отслеживать позицию зонда в любой момент времени, благодаря чему имеется возможность динамической подстройки МПФС. Внешний вид опытного образца измерительной установки показан на рисунке 1.

Рис. 1. Опытный образец установки для измерения магнитного поля МПФС ЛБВ
Выбор алгоритма обработки получаемых данных представляет отдельную задачу. Широко применяемым методом при анализе сигналов является математический аппарат преобразования Фурье. Преобразование Фурье позволяет выполнить переход из временной области представления сигнала в частотную, благодаря чему можно определить гармонический состав сигнала. По результатам преобразования Фурье строится амплитудная характеристика, при необходимости можно также построить фазовую характеристику. Если исследуемый сигнал задан в виде дискретных значений, то используют дискретное преобразование Фурье (ДПФ). Для уменьшения времени расчета ДПФ используют алгоритм быстрого преобразования Фурье (БПФ) [2, 3].
В ходе эксперимента проводились измерения поперечной составляющей магнитного поля входящих в состав МПФС магнитов. Процедура измерений такова, что датчик Холла «сканирует» постоянный магнит по азимуту несколько раз, при этом каждый замер привязывается к конкретной координате при помощи датчика углового положения. Многократный «промер» системы позволяет повысить точность результатов в силу периодичности процедуры измерений, причем получаемые данные также носят периодический характер. Совмещение принятых значений в рамках одного периода позволяет получить набор точек, вплоть до измерения на 1/10 градуса.
Полученные в результате эксперимента данные отражают зависимость поперечной компоненты вектора магнитной индукции B, мТл, от азимутального угла α, ˚. Несовершенство технологии производства постоянных магнитов, а также технологии сборки магнитов в периодическую систему приводит к неравномерности в структуре магнитного поля, т. е. колебаниям модуля вектора магнитной индукции. Выявленным неравномерностям магнитных полей необходимо дать числовую характеристику. В процессе сборки магнитной системы, на этапе, когда выполняется подбор и состыковка магнитов в МПФС такую количественную характеристику можно использовать для отбраковки неподходящих магнитов. В случае подстройки магнитной системы, например, путем взаимного вращения постоянных магнитов друг относительно друга, вновь необходимо оценивать степень неравномерности структуры результирующих магнитных полей, выполняя новую измерительную процедуру.
Подобную числовую характеристику можно вычислить различными методами. Самым простым является подсчет разницы значений максимальной и минимальной измеренной величины. Также, например, можно оценить отклонение от среднеквадратического значения, использовать корреляционный анализ. Каждая методика имеет свои преимущества и недостатки. Вычисление «разброса» величины магнитного поля посредством разницы экстремумов самый простой способ, который, однако не способен выявить частоту колебаний в полученном сигнале. Корреляционный анализ позволяет установить оптимальное взаимное угловое положение постоянных магнитов, однако при расчете требуется нормирование функции корреляции, в результате чего теряется связь с амплитудой сигнала. Математический аппарат преобразования Фурье совмещает в себе универсальность и эффективность при анализе данных.
Расчет ДПФ в комплексной форме выполняется при помощи соотношения (1):
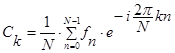 (1)
(1)
где:
fn — измеренное значение модуля магнитной индукции;
k — номер вычисляемого коэффициента Фурье;
N — число точек в выборке;
2π/N — угловая частота сигнала.
В результате проведенного эксперимента был получен набор графиков азимутального распределения магнитного поля для нескольких магнитов, которые представлены на рисунках 1–3. Графики распределения магнитного поля совмещены с соответствующими им спектральными характеристиками, расчет которых был выполнен по формуле 1.
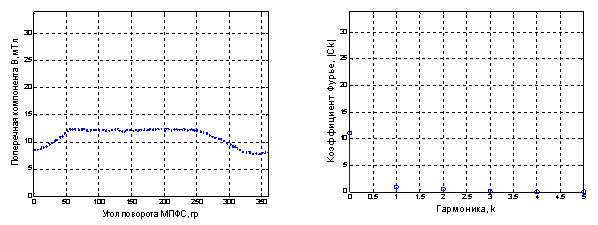
Рис. 2. Азимутальное распределение магнитного поля магнита № 1 и его спектральная характеристика
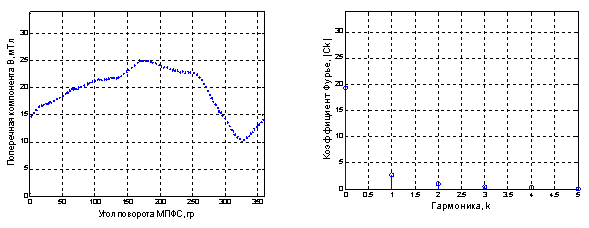
Рис. 3. Азимутальное распределение магнитного поля магнита № 2 и его спектральная характеристика
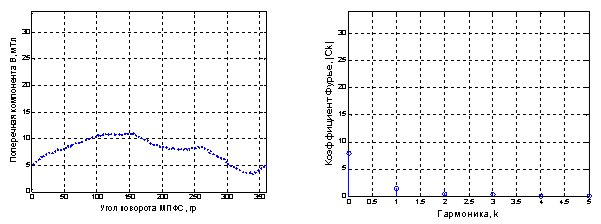
Рис. 4. Азимутальное распределение магнитного поля магнита № 3 и его спектральная характеристика
Спектральная характеристика, представленная на рисунках 1–3 включает 360 точек, что соответствует количеству полученных измерений. В построенном спектре амплитуд информативны первые 6–10 гармоник, остальные составляющие имеют нулевые значения и на рисунках не представлены. Из амплитудного спектра видна доля составляющих частот в сигнале. Нулевая гармоника показывает среднее значение функции, величина остальных гармоник позволяет установить ту числовую характеристику, которую мы искали для оценки степени неравномерности распределения азимутального магнитного поля. Так, для модуля второй гармоники рисунка 1 получено значение 3,79, для рисунка 2 и 3 получены значения модуля 1,49 и 1,4 соответственно. По величине модуля второй и третей гармоник естественно установить критерий неравномерности, своего рода порог прохождения при анализе структуры поля выбранного магнита. В случае если величина модуля второй гармоники при расчете ДПФ превышает установленное значение, магнит отбраковывается.
Алгоритм ДПФ привлекателен и тем, что имеется возможность его аппаратной реализации, т. е. нет необходимости передавать принятый массив точек на ПК, обработку данных может выполнить микропроцессор измерительной установки. Описанные решения позволяют существенно улучшить качество получаемых магнитных систем, а также уменьшить время их сборки. Установка обладает высоким быстродействием, многократные измерения позволяют эффективно выполнять настройку МПФС, алгоритм анализа данных посредством ДПФ устанавливает объективный критерий качества магнитного поля формируемого каждым магнитом. Преобразование Фурье можно использовать и для контроля продольной составляющей магнитного поля, хотя спектральная характеристика будет несколько сложнее.
Литература:
1. Гилмор А. С. Лампа с бегущей волной. / А. С. Гилмор: пер. с англ. Кудряшова А. Г. — М.: Техносфера, 2013. — 616 с.
2. Сато Юкио. Без паники! Цифровая обработка сигналов. / Юкио Сато: пер. с яп. Селиной Т. Г. — М.: Додэка-ХХI, 2010. — 176 с.
3. Ричард Лайонс. Цифровая обработка сигналов. / Лайонс Ричард: пер. с англ. Под редакцией Бритова А. А. — М.: ООО «Бином-Пресс», 2006. — 656 с.







