Введение
Исследования нанокомпозитных материалов, содержащих агрегаты плазмонно-резонансных наночастиц, приобрели особую актуальность в связи с обнаружением у них ряда уникальных оптических свойств и возможности многочисленных приложений [1–5].
При этом агрегаты с локально анизотропной структурой обладают свойством гигантского усиления пространственно локализованных электромагнитных полей вблизи частиц, резонансных внешнему электромагнитному полю. Появление высокодобротных оптических резонансов наночастиц связано с возбуждением поверхностных плазмонов, а само усиление наблюдается в области неоднородно уширенной полосы плазмонного поглощения.
За десятилетия, прошедшие с начала этих исследований, накоплен большой объем экспериментальных данных и выявленных закономерностей по воздействию импульсного лазерного излучения на такие материалы, который не получил должного объяснения в силу сложности и взаимосвязанности сопутствующих процессов. Эти процессы охватывают взаимосвязанные термодинамические, оптические, физико-химические, механические и другие явления.
В [6] представлен обзор работ с результатами экспериментальных исследований, в которых были обнаружены нетривиальное проявление разнообразных нелинейно-оптических процессов в агрегированных наноколлоидах благородных металлов, а также фотохромные реакции, лежащие в основе эффекта оптической памяти нанокомпозитов.
Одним из важных факторов, влияющих на физические процессы в импульсных полях, является продолжительность воздействия оптического излучения на резонансные частицы коллоидных агрегатов. Такие процессы могут сопровождаться как нереверсивным сдвигом соседних наночастиц в резонансных доменах агрегатов, так и утратой резонансных свойств наночастиц при их нагреве и плавлении.
В данной работе проведен анализ основных механизмов, лежащих в основе процесса взаимодействия многочастичного агрегата, состоящего из металлических наночастиц, с лазерным излучением с частотой, лежащей в области плазменного поглощения этих частиц.
В работе [7] была представлена модель оптодинамических явлений в коллоидных агрегатах, состоящих из связанных металлических частиц, которые подвергаются воздействию импульсного лазерного излучения пикосекундной длительности. Эти явления определяют оптические отклики нанокомпозитных материалов и наноколлоидов на действие импульсного лазерного излучения.
Математическая модель
Вкратце остановимся на описании данной модели [7]. Процесс взаимодействия лазерного излучения с коллоидным агрегатом описывается следующей системой уравнений:
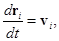
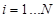 (1)
(1)
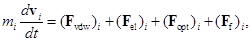 (2)
(2)
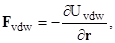
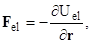
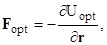 (3)
(3)
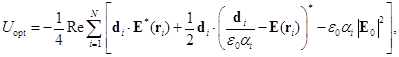 (4)
(4)
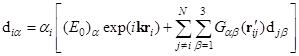 ,
, 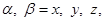 (5)
(5)
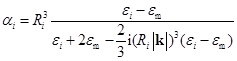 , (6)
, (6)
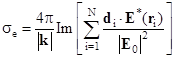 ,
, 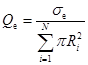 , (7)
, (7)
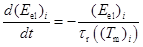 ,
, 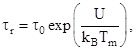 (8)
(8)
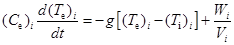 ,
, 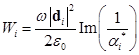 , (9)
, (9)
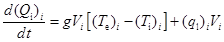 , (10)
, (10)
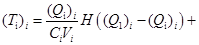
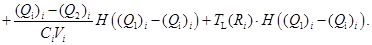 (11)
(11)
Здесь 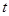 – время, прошедшее с начала действия лазерного импульса,
– время, прошедшее с начала действия лазерного импульса, 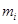 ,
, 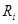
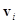 ,
, 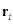 ;
; 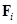 – соответственно, масса, радиус, скорость, радиус-вектор центра масс и равнодействующая всех сил
– соответственно, масса, радиус, скорость, радиус-вектор центра масс и равнодействующая всех сил 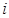 -й частицы;
-й частицы; 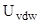 – энергия ван-дер-ваальсова взаимодействия;
– энергия ван-дер-ваальсова взаимодействия; 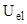 – энергия упругого взаимодействия, обусловленная деформацией полимерных адсорбционных слоев (АС) частиц;
– энергия упругого взаимодействия, обусловленная деформацией полимерных адсорбционных слоев (АС) частиц; 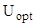 – энергия взаимодействия светоиндуцированных диполей как между собой, так и с внешним полем;
– энергия взаимодействия светоиндуцированных диполей как между собой, так и с внешним полем; 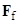 – сила (Стокса) вязкого трения;
– сила (Стокса) вязкого трения; 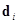 – индуцированный локальным полем дипольный момент частицы, определяемый методом связанных диполей [7];
– индуцированный локальным полем дипольный момент частицы, определяемый методом связанных диполей [7]; 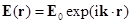 – напряженность электрического поля лазерного излучения (
– напряженность электрического поля лазерного излучения (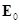 – амплитуда поля);
– амплитуда поля); 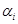 – дипольная поляризуемость частицы;
– дипольная поляризуемость частицы; 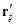 – вектор, соединяющий центры частиц с поправкой на коэффициент пересечения;
– вектор, соединяющий центры частиц с поправкой на коэффициент пересечения; 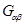 – тензор межчастичного взаимодействия;
– тензор межчастичного взаимодействия; 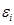 – диэлектрическая проницаемость частицы, в которой релаксационный член зависит от температуры, агрегатного состояния и размера частицы;
– диэлектрическая проницаемость частицы, в которой релаксационный член зависит от температуры, агрегатного состояния и размера частицы; 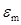 – диэлектрическая проницаемость окружающей среды;
– диэлектрическая проницаемость окружающей среды; 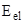 – модуль упругости АС;
– модуль упругости АС; 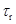 – время релаксации молекулярных связей АС;
– время релаксации молекулярных связей АС; 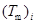 – средняя температура прогретой области около
– средняя температура прогретой области около 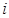 -ой частицы;
-ой частицы; 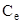 – объемная теплоемкость электронной компоненты;
– объемная теплоемкость электронной компоненты; 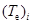 ,
, 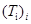 – соответственно, температура электронной и ионной компоненты i-ой частицы;
– соответственно, температура электронной и ионной компоненты i-ой частицы; 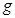 – скорость энергетического обмена между электронной и ионной подсистемами;
– скорость энергетического обмена между электронной и ионной подсистемами; 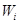 – поглощаемая частицей мощность лазерного излучения;
– поглощаемая частицей мощность лазерного излучения; 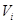 – объем частицы;
– объем частицы; 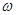 – циклическая частота лазерного излучения;
– циклическая частота лазерного излучения; 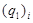 – тепловой поток на единицу объема, описывающий тепловые потери;
– тепловой поток на единицу объема, описывающий тепловые потери; 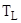 – температура плавления наночастицы. Для учета плавления вместо уравнения для температуры ионной подсистемы частицы используется уравнение (11) для тепловой энергии
– температура плавления наночастицы. Для учета плавления вместо уравнения для температуры ионной подсистемы частицы используется уравнение (11) для тепловой энергии 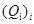 ионной подсистемы. В уравнении (11):
ионной подсистемы. В уравнении (11): 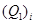 – тепловая энергия, соответствующая началу плавления частицы;
– тепловая энергия, соответствующая началу плавления частицы; 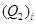 – тепловая энергия, соответствующая окончанию плавления частицы.
– тепловая энергия, соответствующая окончанию плавления частицы.
Важным фактором, который влияет на оптодинамические процессы, индуцированные внешним излучением в резонансном домене, является локальное окружение частиц домена другими частицами [8], которое определяет оптические характеристики данного домена. Под резонансным доменом многочастичного агрегата подразумевается группа близкорасположенных частиц в агрегате, резонансная частота которой совпадает с частотой внешнего излучения. В нашем случае близость частицы к резонансу определяется по максимальному значению наведенного внешним полем дипольного момента. В работе исследуются несколько типов резонансных доменов (моно- и полидисперсных димеров и тримеров (см. рис. 1 в [8])), подвергающихся воздействию лазерного излучения, поляризованного вдоль оси домена.
В соответствии с представлениями [7, 8], физическая картина взаимодействия домена с лазерным излучением выглядит следующим образом. До начала воздействия лазерного импульса частицы в домене находятся в положении устойчивого равновесия ван-дер-ваальсовых и упругих сил (последние обусловлены деформацией полимерных адсорбционных слоев наночастиц). Лазерное излучение высокой интенсивности в импульсных полях пикосекундной длительности порождает светоиндуцированные оптические силы, однако они действуют лишь в течение импульса и не вносят существенный вклад в фотомодификацию домена. В полях наносекундной длительности, при которых также наблюдаются фотохромные эффекты, интенсивность слишком низка для появления заметных оптических сил. Тем не менее, поглощение доменом излучения приводит к нагреву его наночастиц (электронной и ионной компонент металла) и передаче тепловой энергии полимерному адсорбционному слою (АС). Вследствие его нагрева происходит уменьшение модуля упругости АС. Это сопровождается нарушением баланса сил и сближением частиц под действием ван-дер-ваальсова притяжения (вплоть до полного контакта их металлических поверхностей). В свою очередь, изменение межчастичного зазора в домене после окончания импульса (или во время действия импульса) проявляется в сдвиге максимума полосы плазмонного поглощения домена относительно длины волны лазерного излучения. В случае пикосекундных импульсов это приводит к статическим изменениям в спектре, сохраняющихся и после окончания действия импульса. То есть механизм воздействия излучения на положение частиц в домене реализуется через нагрев частиц и изменение свойств их АС.
Кроме того учитывается то, что нагрев и плавление металлического ядра частиц приводит к увеличению константы электронной релаксации свободных электронов, что приводит к снижению добротности плазмонного резонанса, а, значит, также и к изменению взаимодействия лазерного изучения с доменом при ухудшении резонансных свойств системы. Это является причиной динамических спектральных изменений, проявляющихся лишь за время действия пикосекундного импульса.
В предложенной в [7] оптодинамической модели взаимодействия резонансного домена с импульсным лазерным излучением учитывается достаточно широкий ряд взаимосвязанных термодинамических, оптических, физико-химических и механических процессов. Реализация модели воспроизводит наиболее реалистичную картину воздействия импульсного лазерного излучения на резонансный домен по сравнению с уже имеющимися оптодинамическими моделями [9] и включает в себя ранее неучтенные физические процессы и явления [6, 10].
С помощью данной оптодинамической модели получены следующие результаты.
На рис. 1 представлена зависимость от длительности лазерного импульса максимальной температуры (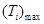 ) ионной компоненты наночастицы, при которой достигается статическая фотомодификация Ag димера (сближение частиц). Особенности поведения данной кривой объясняются кинетикой изменения модуля упругости АС частиц. Скорость изменения модуля упругости АС частиц возрастает с ростом температуры ионной компоненты материала частиц
) ионной компоненты наночастицы, при которой достигается статическая фотомодификация Ag димера (сближение частиц). Особенности поведения данной кривой объясняются кинетикой изменения модуля упругости АС частиц. Скорость изменения модуля упругости АС частиц возрастает с ростом температуры ионной компоненты материала частиц 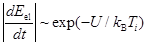 [6]. Из этого соотношения следует уменьшение температуры
[6]. Из этого соотношения следует уменьшение температуры 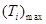 с ростом длительности импульса: для фотомодификации при малых длительностях импульса требуется высокая температура, чтобы модуль упругости АС успел уменьшиться за время импульса до значения, достаточного для сближения частиц под действием ван-дер-ваальсова притяжения и проявления статической модификации домена. Однако в диапазоне τ = 2∙10−6–10−5 с
с ростом длительности импульса: для фотомодификации при малых длительностях импульса требуется высокая температура, чтобы модуль упругости АС успел уменьшиться за время импульса до значения, достаточного для сближения частиц под действием ван-дер-ваальсова притяжения и проявления статической модификации домена. Однако в диапазоне τ = 2∙10−6–10−5 с 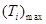 опускается до температуры плавления частиц и ниже. Проявление фотомодификации в этом диапазоне зависит не от максимально достигаемой температуры, а от скорости ее изменения
опускается до температуры плавления частиц и ниже. Проявление фотомодификации в этом диапазоне зависит не от максимально достигаемой температуры, а от скорости ее изменения 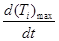 .
.
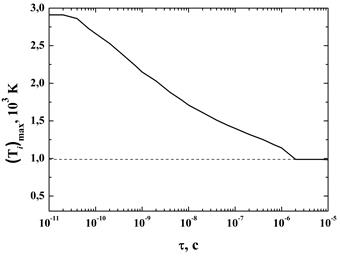
Рис. 1. Зависимость максимальной ионной температуры (Ti) частиц
монодисперсного Ag димера (радиусы частиц 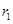 =
=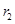 = 5 нм), достигаемой при воздействии
= 5 нм), достигаемой при воздействии
импульса с пороговой интенсивностью, от длительности импульса.
Пунктирная линия показывает температуру плавления частиц
Из рис. 1 видно, что в диапазоне τ = 10−11–10−10 c максимальная температура меняется слабо. Это объясняется конечной скоростью обмена между электронной и ионной компонентой. Если при больших длительностях импульса температура ионной компоненты материала частицы начинает уменьшаться сразу после окончания действия, то в случае импульсов малой длительности эта температура продолжает расти и после окончания действия импульса за счет энергии, запасенной в электронной компоненте материала частицы.
При длительности импульса меньшей эффективного времени теплообмена между электронной и ионной компонентой (τ < 10−11–10−10 c) процесс взаимодействия лазерного импульса с частицами можно рассматривать состоящим из двух этапов. Вначале происходит относительно быстрая передача энергии лазерного импульса электронной компоненте, температура которой не влияет на динамику модуля упругости АС частицы. Уже после этого имеет место относительно медленный процесс передачи энергии от электронной компоненты к ионной. В таких условиях это приводит к тому, что динамика нагрева не зависит от длительности импульса при соответствии плотности энергии импульса пороговой, то есть достаточной для статической фотомодификации вследствие плавления АС частиц.
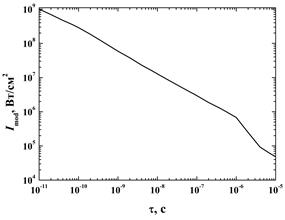
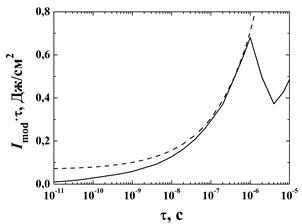
На рис. 2 представлены зависимости от длительности импульса значений интенсивности (а) и плотности энергии импульса (б), при достижении которых проявляется статическая модификация.
(а) (б)
Рис. 2. Зависимость от длительности импульса пороговых значений интенсивности (а)
и плотности энергии излучения (сплошная линия) с аппроксимационными
значениями (12) (пунктир) (б), соответствующими статическому порогу
фотомодификации монодисперсного Ag димера
Для объяснения роста пороговой плотности энергии (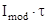 ) с увеличением длительности импульса в диапазоне
) с увеличением длительности импульса в диапазоне 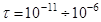 с на рис. 2(б) необходимо учесть следующее.
с на рис. 2(б) необходимо учесть следующее.
Во-первых, потери энергии нагреваемой частицы (Q) вблизи максимальной температуры ионной компоненты 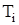 определяются теплопотерей в окружающую среду. Во-вторых,
определяются теплопотерей в окружающую среду. Во-вторых, 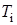 должна достигать значений, при которых за время порядка длительности импульса упругость АС успевает существенно уменьшиться. То есть, длительность импульса τ и время релаксации τr АС должны быть одного порядка:
должна достигать значений, при которых за время порядка длительности импульса упругость АС успевает существенно уменьшиться. То есть, длительность импульса τ и время релаксации τr АС должны быть одного порядка:
Таким образом, вводя подгоночные параметры A и W0, получаем следующее выражение:
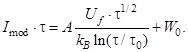 (12)
(12)
Значения этих параметров А ≈ 0.67 Дж/К·см2·с1/2, W0 ≈ 0.06 Дж/см2 выбирались таким образом, чтобы в диапазоне 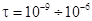 с достигалось наилучшее совпадение аппроксимационной зависимости (12) с зависимостью Imod(τ)∙τ, полученной численно с помощью оптодинамической модели. В этом диапазоне частицы находятся в жидком состоянии, а это означает, что из-за существенного ослабления их резонансных свойств взаимодействие излучения с ними происходит при значительно более низком сечении поглощения.
с достигалось наилучшее совпадение аппроксимационной зависимости (12) с зависимостью Imod(τ)∙τ, полученной численно с помощью оптодинамической модели. В этом диапазоне частицы находятся в жидком состоянии, а это означает, что из-за существенного ослабления их резонансных свойств взаимодействие излучения с ними происходит при значительно более низком сечении поглощения.
Расхождение расчетной и аппроксимационной кривых как на малых (< 10−9 с), так и больших (> 10−6 с) временах (рис. 2(б)), на которых у аппроксимационной зависимости продолжается монотонный рост, связано с большей, чем в диапазоне (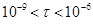 с) величиной сечения поглощения. В первом случае (
с) величиной сечения поглощения. В первом случае (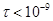 с) это связано с тем, что частица не успевает перейти в жидкое состояние за время действия импульса (сечение поглощения максимально и порог фотомодификации Imod∙τ низкий). Во втором случае (
с) это связано с тем, что частица не успевает перейти в жидкое состояние за время действия импульса (сечение поглощения максимально и порог фотомодификации Imod∙τ низкий). Во втором случае (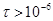 с) с уменьшением соотношения жидкой и твердой фазы в материале частицы (ее приближением к полной кристаллизации) сечение поглощения также растет по мере увеличения длительности импульса. Большое сечение поглощения означает и более эффективное использование энергии лазерного излучения в условиях резонанса. Рост же пороговой плотности энергии на промежуточных временах (
с) с уменьшением соотношения жидкой и твердой фазы в материале частицы (ее приближением к полной кристаллизации) сечение поглощения также растет по мере увеличения длительности импульса. Большое сечение поглощения означает и более эффективное использование энергии лазерного излучения в условиях резонанса. Рост же пороговой плотности энергии на промежуточных временах (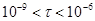 с) в основном определяется температурой, которая необходима для плавления АС за время импульса. Эти же объяснения справедливы для дальнейшего повышения пороговой плотности энергии в диапазоне
с) в основном определяется температурой, которая необходима для плавления АС за время импульса. Эти же объяснения справедливы для дальнейшего повышения пороговой плотности энергии в диапазоне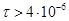 с, когда плавление частиц отсутствует.
с, когда плавление частиц отсутствует.
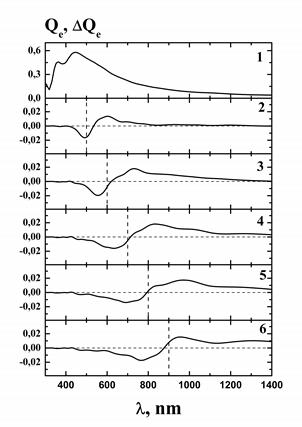
На рис. 3 представлен результат воздействия лазерного импульса пикосекундной длительности на монодисперсные (рис. 3 (а)) и полидисперсные (рис. 3 (б)) агрегаты, проявляющий себя через значительное время после окончания импульса (так называемая «статическая модификация»).
Подчеркнем, что на рис. 3 вид дифференциальных спектров, индуцированных пикосекундным импульсом, сохраняется на временах до десятков наносекунд. Объяснение дальнейшей незначительной эволюции этих спектров прежде всего при воздействии наносекундными импульсами требует отдельных исследований.
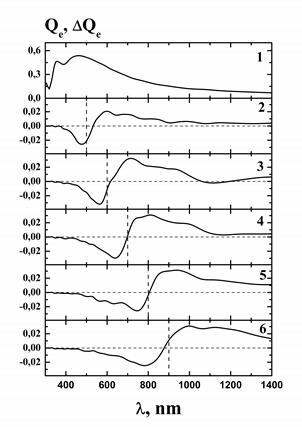
(а) (б)
Рис. 3. Статическая фотомодификация. Спектры экстинкции монодисперсных (а)
и полидисперсных (б) агрегатов, состоящих из 50 частиц.
(1) — исходный спектр, (2)–(6) – разностные спектры экстинкции,
полученные через t = 5 нс после начала импульса. Длина волны лазерного излучения
(2) – 500 нм, (3) – 600 нм, (4) – 700 нм, (5) – 800 нм, (6) – 900 нм.
Длительность импульса 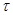 = 20 пс, интенсивность излучения
= 20 пс, интенсивность излучения 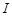 = 7.5∙108 Вт/см2,
= 7.5∙108 Вт/см2,
радиусы частиц (а) – 5 нм, (б) – от 2 до 8 нм
Как видно из представленных рисунков, процесс модификации агрегатов обладает спектральной селективностью. Однако данная селективность обладает рядом особенностей.
Наиболее важная из них — смещение центра провала в коротковолновую область спектра относительно лазерной длины волны. При этом смещение тем больше, чем больше длина волны лазерного излучения. Причина такого сдвига провала заключается в механизме статической модификации. Результатом воздействия лазерного излучения на резонансные домены с максимумами спектра поглощения, лежащими близко к лазерной длине волны, является сближение частиц домена и, как следствие, смещение максимумов спектра поглощения в длинноволновый диапазон. Таким образом, резонансы, находящиеся в коротковолновой области от лазерной длины волны, спектрально замещают резонансы, находящиеся с длинноволновой стороны. При этом чем больше резонансная длина волны домена, тем шире спектр поглощения, а, соответственно, увеличивается и спектральный диапазон модификации, что приводит к большему смещению провала относительно лазерной длины волны.
Кроме того, следствием уширения спектра поглощения каждого резонансного домена при увеличении его резонансной длины волны является вторая особенность представленных результатов — увеличение ширины провала при увеличении длины волны воздействующего лазерного излучения.
Сравнивая процесс модификации в монодисперсных и полидисперсных агрегатах, следует отметить, что глубина спектрального провала у полидисперсных агрегатов значительно больше, чем у монодисперсных. Связано это с тем, что порог статической модификации у резонансных доменов, включающих в себя малые частицы, значительно ниже, чем у доменов, включающих в себя только частицы среднего размера.
В результате применения разработанной модели получены зависимости основных пороговых характеристик процесса фотомодификации коллоидных агрегатов от длительности лазерного импульса. Получены сведения об основных закономерностях фотомодификации многочастичных агрегатов. Показаны особенности модификации полидисперсных агрегатов.
Литература:
1. Kreibig U. Optical properties of metal clusters / U. Kreibig, M. Vollmer. Berlin: Springer Verlag, 1995. – P. 533.
2. Shalaev V.M. Electromagnetic properties of small-particle composites // Physics Reports, 1996. – V. 272. – P. 61–137.
3. Shalaev V.M. Nonlinear Optics of Random Media: Fractal Composites and Metal-Dielectric Films / V.M. Shalaev. Berlin: Springer Verlag, 2000.
4. Карпов С.В. Слабко В.В. Оптические и фотофизические свойства фрактально-структурированных золей металлов / С. В. Карпов, В. В. Слабко. Новосибирск: Российская академия наук, Сибирское отделение, 2003.
5. Stockman M.I., Pandey L.N., George T.F. Enhanced Nonlinear-Optical Responses of Disordered Clusters and Composites // Nonlinear Optical Materials. New York: Springer-Verlag, 1998.
6. Gavrilyuk A.P., Karpov S.V. Processes in resonant domains of metal nanoparticle aggregates and optical nonlinearity of aggregates in pulsed laser fields // Applied Physics B. 2009. – V. 97. – P.163–173.
7. Ershov A.E., Gavrilyuk A.P., Karpov S.V., Semina P.N. Optodynamic phenomena in aggregates of polydisperse plasmonic nanoparticles // Applied Physics B. 2014. – V. 115, No. 8. – P. 547–560.
8. Ershov A.E., Gavrilyuk A.P., Karpov S.V., Semina P.N. Property of local environment in resonant domains of polydisperse plasmonic nanoparticle aggregates on optodynamic processes in pulsed laser fields // Chinese Physics B. 2015. – V. 24, No. 4. – P. 047804
9. Ganeev R.A., Ryasnyansky A I., Kamalov S R., Usmanov T B. Nonlinear susceptibilities, absorption coefficients and refractive indices of colloidal metals // Phys. D: Appl. Phys. 2001. – V. 34. – P. 1602.
10. Данилова Ю.Э., Драчёв В.П., Перминов С.В., Сафонов В.П. Нелинейность коэффициентов преломления и поглощения металлических фрактальных кластеров в коллоидных растворах.// Известия РАН сер. физич. 1996. – Т. 60, № 3. – C. 18–22.







