Введение
Современные технологии добычи полезных ископаемых, производства и обработки материалов требуют более полного и точного описания процессов тепломассобмена в жидкостях и газах. Данные среды зачастую являются многокомпонентными. В многокомпонентных системах имеет место ряд процессов переноса тепла и массы: конвекция, теплопроводность, основная и перекрестная диффузии, термодиффузия. Явление термодиффузии (эффекта Соре) связано с возникновением потока массы под действием градиента температуры [1]. Этот эффект играет важную роль во многих природных и технологических процессах (конвекция в смесях, распределение углеводородов в природных месторождениях, разделение изотопов и др.) [2, 3].
Для описания и предсказания термодиффузионных процессов необходимо знать коэффициенты переноса (в том числе диффузии и термодиффузии). Одним из экспериментальных методов их измерения является термодиффузионная колонна, которая представляет собой вертикальный слой между двумя твердыми стенками, поддерживаемыми при различных температурах. Колонны могут иметь плоскую (слой между двумя плоскими стенками), а также цилиндрическую (слой между коаксиальными цилиндрами) формы. Термодиффузионное разделение смеси под действием горизонтального градиента температуры, и вертикальный конвективный поток приводят к возникновению вертикальных градиентов концентрации. Измерение этих градиентов путем отбора проб на различных уровнях по высоте колонны позволяет определить коэффициенты термодиффузии. Необходимым условием проведения измерений в колонне является устойчивость стационарного конвективного течения [4, 5]. В настоящее время устойчивость такого течения исследована лишь для плоских колонн относительно двумерных возмущений [5–7]. В работах [8, 9] был обнаружен эффект устойчивого вертикального разделения бинарной смеси в цилиндрической колонне для аномального эффекта Соре при достаточно больших разностях температур между стенками (в этом случае тяжелый компонент накапливается в верхней части колонны, что создает потенциально неустойчивую стратификацию). Этот эффект до сих пор не получил теоретического объяснения. Таким образом, вопрос стационарного разделения и его устойчивости для бинарных и многокомпонентных смесей в цилиндрических колоннах в настоящее время остается открытым.
В данной работе проводится исследование процесса разделения многокомпонентной смеси в цилиндрической термодиффузионной колонне. Исследование выполнено в цилиндрических координатах для учета влияния отношения радиусов цилиндров и их кривизны на процесс разделения. Построены точные решения задачи, имеющие различный вид в зависимости от значения управляющих параметров, выполнено сравнение результатов с результатами для плоской колонны.
Постановка задачи
Рассмотрим процесс разделения смеси из 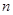 компонентов в цилиндрической термодиффузионной колонне. Пусть компонент
компонентов в цилиндрической термодиффузионной колонне. Пусть компонент 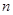 выбран в качестве растворителя, тогда состав смеси можно задать вектором массовых долей
выбран в качестве растворителя, тогда состав смеси можно задать вектором массовых долей 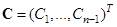 , где
, где 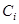 –концентрация компонента
–концентрация компонента 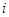 , при этом
, при этом 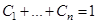 . Для описания смеси будем использовать модель Обербека-Буссинеска с уравнением состояния
. Для описания смеси будем использовать модель Обербека-Буссинеска с уравнением состояния
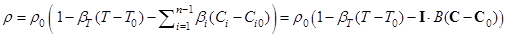 .
.
Здесь 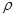 – плотность,
– плотность, 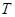 – температура,
– температура, 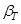 – коэффициент теплового расширения,
– коэффициент теплового расширения, 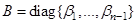 – диагональная матрица коэффициентов концентрационного расширения, индекс «0» соответствует средним значениям температуры и концентрации.
– диагональная матрица коэффициентов концентрационного расширения, индекс «0» соответствует средним значениям температуры и концентрации.
Уравнения движения смеси с учетом силы тяжести с вектором ускорения свободного падения 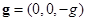 имеют вид
имеют вид
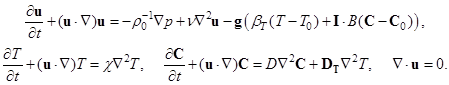 (1)
(1)
В приведенных выражениях 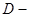 матрица коэффициентов диффузии размерности
матрица коэффициентов диффузии размерности 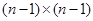 ,
, 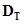 – вектор коэффициентов термодиффузии размерности
– вектор коэффициентов термодиффузии размерности 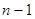 ,
, 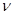 и
и 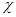 – коэффициенты кинематической вязкости и температуропроводности соответственно,
– коэффициенты кинематической вязкости и температуропроводности соответственно, 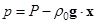 – отклонение полного давления
– отклонение полного давления 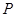 от гидростатического,
от гидростатического, 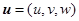 – вектор скорости,
– вектор скорости, 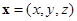 – вектор координат.
– вектор координат.
Рассмотрим процесс разделения в термодиффузионной колонне высотой 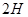 , которая представляет собой вертикальный слой между коаксиальными цилиндрами с радиусами
, которая представляет собой вертикальный слой между коаксиальными цилиндрами с радиусами 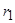 и
и 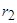 ,
, 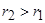 (рис. 1). Введем цилиндрические координаты
(рис. 1). Введем цилиндрические координаты 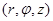 . Если отношение высоты колонны к зазору между цилиндрами
. Если отношение высоты колонны к зазору между цилиндрами 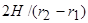 имеет порядок 102 или более, то конвективное течение строго вертикально (кроме небольших областей вверху и внизу колонны, которыми мы в дальнейшем пренебрегаем). Тогда из уравнения неразрывности следует, что вертикальная скорость зависит только от радиальной координаты. Предполагается, что вертикальные градиенты концентрации постоянны [4, 5], поэтому стационарное решение, описывающее конвекцию и разделение смеси в колонне, ищется в виде:
имеет порядок 102 или более, то конвективное течение строго вертикально (кроме небольших областей вверху и внизу колонны, которыми мы в дальнейшем пренебрегаем). Тогда из уравнения неразрывности следует, что вертикальная скорость зависит только от радиальной координаты. Предполагается, что вертикальные градиенты концентрации постоянны [4, 5], поэтому стационарное решение, описывающее конвекцию и разделение смеси в колонне, ищется в виде:
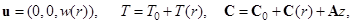 (2)
(2)
где 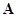 – вектор постоянных вертикальных градиентов концентрации. На границах ставятся условия прилипания, отсутствия диффузионного потока, и задаются различные постоянные температуры:
– вектор постоянных вертикальных градиентов концентрации. На границах ставятся условия прилипания, отсутствия диффузионного потока, и задаются различные постоянные температуры:
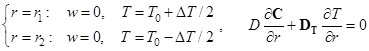 . (3)
. (3)
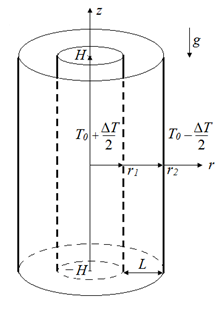
Рис. 1. Схема цилиндрической термодиффузионной колонны
Для замкнутой колонны в стационарном состоянии расход смеси и полный поток массы компонентов через поперечное сечение 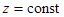 должны быть равны нулю. Эти условия, а также условие сохранения массы компонентов смеси, записываются так:
должны быть равны нулю. Эти условия, а также условие сохранения массы компонентов смеси, записываются так:
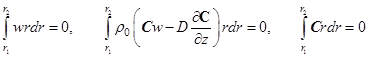 . (4)
. (4)
Предполагается, что вертикальная конвекция достаточно интенсивная и диффузионный перенос массы в вертикальном направлении пренебрежимо мал по сравнению с конвективным переносом. Тогда второе условие из (4) сводится к уравнению
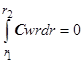 .
.
Введем безразмерные переменные (со штрихом) и некоторые соотношения:

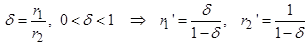 .
.
В безразмерных переменных система уравнений (1) принимает вид
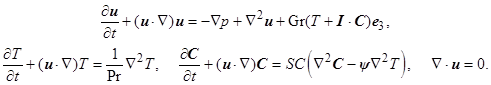 (5)
(5)
Решение для концентрации в безразмерном форме представимо так: 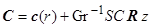 (штрих здесь и далее опущен), где
(штрих здесь и далее опущен), где 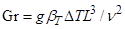 – число Грасгофа,
– число Грасгофа, 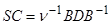 ,
, 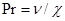 – число Прандтля,
– число Прандтля, 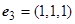 ,
, 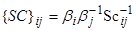 ,
, 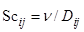 – числа Шмидта,
– числа Шмидта, 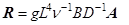 – вектор безразмерных параметров, называемых концентрационными числами Рэлея. Вектор
– вектор безразмерных параметров, называемых концентрационными числами Рэлея. Вектор 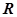 характеризует вертикальное разделение смеси.
характеризует вертикальное разделение смеси.
Граничные условия (3) и соотношения (4) в безразмерной форме принимают вид
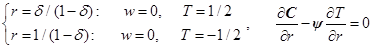 , (6)
, (6)
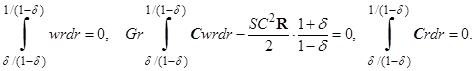 (7)
(7)
Здесь 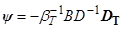 – вектор отношений разделения. Данный вектор характеризует отношение градиентов плотности, вызванных градиентами концентрации и температуры, в замкнутой системе в условиях механического равновесия.
– вектор отношений разделения. Данный вектор характеризует отношение градиентов плотности, вызванных градиентами концентрации и температуры, в замкнутой системе в условиях механического равновесия.
Если диффузия в вертикальном направлении не учитывается, для второго условия из (7) получим
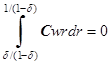 . (8)
. (8)
Построение решения
Введем функцию тока
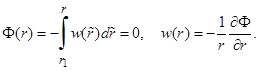 (9)
(9)
Подставим общий вид решения (2) в безразмерных переменных в систему (5). Продифференцировав ее еще раз, получим следующую систему уравнений:
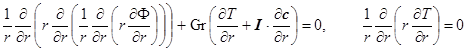 ,
,
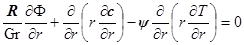 . (10)
. (10)
Поля температуры и концентрации определяются соответственно из второго и третьего уравнений системы (10) с учетом условий (6)–(8):
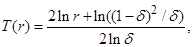 (11)
(11)
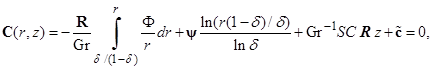 (12)
(12)
где 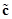 – постоянный вектор.Подставив полученные выражения (11) и (12) в систему (10), приходим к задаче для функции тока:
– постоянный вектор.Подставив полученные выражения (11) и (12) в систему (10), приходим к задаче для функции тока:
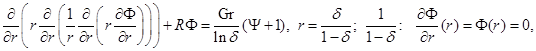 (13)
(13)
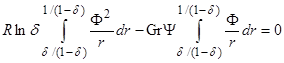 (14)
(14)
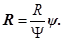 (15)
(15)
Здесь 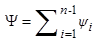 – суммарное отношение разделения,
– суммарное отношение разделения, 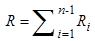 – суммарное концентрационное число Рэлея.
– суммарное концентрационное число Рэлея.
Решение задачи (13), (14) имеет различный вид в зависимости от значений управляющих параметров.
Предположим, что 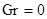 . В данном случае конвекция и вертикальные градиенты концентраций отсутствуют (
. В данном случае конвекция и вертикальные градиенты концентраций отсутствуют (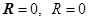 ). Это следует из условия равенства нулю полных потоков массы компонентов смеси через произвольное поперечное сечение колонны (в этом условии необходимо учитывать вклад вертикальной диффузии, так как конвекция отсутствует). Тогда из (13) и (14) следует также, что и
). Это следует из условия равенства нулю полных потоков массы компонентов смеси через произвольное поперечное сечение колонны (в этом условии необходимо учитывать вклад вертикальной диффузии, так как конвекция отсутствует). Тогда из (13) и (14) следует также, что и 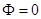 . Таким образом, решение задачи имеет вид
. Таким образом, решение задачи имеет вид
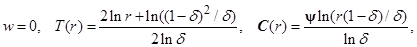 (16)
(16)
при условии, что 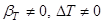 . Равенство
. Равенство 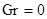 возможно лишь при
возможно лишь при 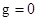 , то есть в невесомости. Профили температуры в безразмерном виде для различных значениях отношения радиусов
, то есть в невесомости. Профили температуры в безразмерном виде для различных значениях отношения радиусов 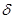 показаны на рис. 1.
показаны на рис. 1.
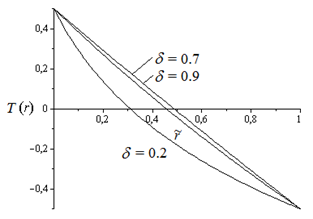
Рис. 1. Профили температуры (в безразмерном виде) в зависимости от 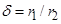
В выражении для температуры была произведена замена
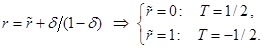 (17)
(17)
При  профиль температуры сходится к линейному, который соответствует плоской колонне.
профиль температуры сходится к линейному, который соответствует плоской колонне.
Рассмотрим случай, когда влияние неоднородности плотности, вызванной изменением концентрации смеси, на конвективное течение смеси пренебрежимо мало (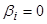 ). Данное предположение справедливо при небольшом суммарном отношении разделения (в работе [10] указан диапазон
). Данное предположение справедливо при небольшом суммарном отношении разделения (в работе [10] указан диапазон 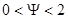 для бинарных смесей). В этом случае в уравнении импульса системы (1) можно пренебречь слагаемым, содержащим вектор концентраций. Для системы (10) в безразмерных переменных получим
для бинарных смесей). В этом случае в уравнении импульса системы (1) можно пренебречь слагаемым, содержащим вектор концентраций. Для системы (10) в безразмерных переменных получим
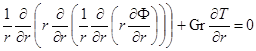 .
.
Поле температуры определяется выражением (11). Используя это выражение, найдем решение для функции тока в виде
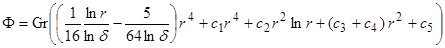 ,
,
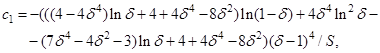
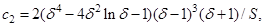
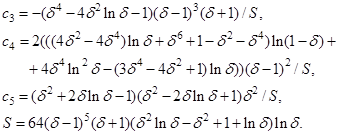
Поля скорости и концентрации определяются из (9) и (12) соответственно как
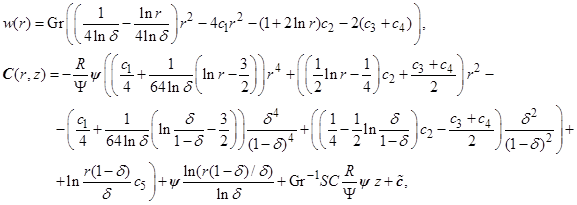
где вектор 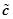 определяется из последнего условия (7). Профиль скорости
определяется из последнего условия (7). Профиль скорости 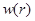 в безразмерной форме для
в безразмерной форме для 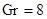 показан на рис. 2. Здесь и далее введена замена (17).
показан на рис. 2. Здесь и далее введена замена (17).
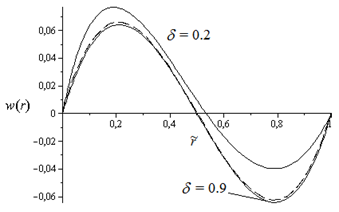
Рис. 2. Профиль скорости в безразмерном виде для различных  при
при  .
.
Профиль скорости для плоской колонны показан штриховой линией
Из рис. 2 видно, что профиль скорости существенно зависит от отношения радиусов  . При
. При 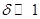 смесь у горячей стенки движется вверх с большей скоростью, чем вниз у холодной. При
смесь у горячей стенки движется вверх с большей скоростью, чем вниз у холодной. При  кривая для цилиндрической колонны приближается к кривой для плоского слоя, которая показана штриховой линией.
кривая для цилиндрической колонны приближается к кривой для плоского слоя, которая показана штриховой линией.
Исследуем соотношение (15) векторов 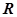 и
и 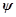 , характеризующее связь между вертикальным разделением смеси и коэффициентами диффузии и термодиффузии. Коэффициент пропорциональности
, характеризующее связь между вертикальным разделением смеси и коэффициентами диффузии и термодиффузии. Коэффициент пропорциональности 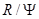 может быть определен с помощью уравнения (14). На рис. 3 показана зависимость
может быть определен с помощью уравнения (14). На рис. 3 показана зависимость 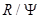 от отношения радиусов цилиндров
от отношения радиусов цилиндров 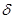 .
.
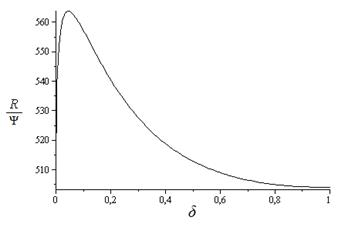
Рис. 3. 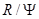 в зависимости от
в зависимости от 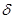
При  предельное значение
предельное значение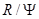 равно 504, т. е.
равно 504, т. е. 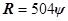 . Данное соотношение согласуется с ранее известным соотношением для плоской колонны [4, 5]. Таким образом, вертикальные градиенты концентрации в данном решении даются формулами:
. Данное соотношение согласуется с ранее известным соотношением для плоской колонны [4, 5]. Таким образом, вертикальные градиенты концентрации в данном решении даются формулами:
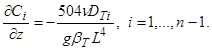
Профиль концентрации 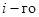 компонента смеси вдоль радиальной координаты представлен отношением
компонента смеси вдоль радиальной координаты представлен отношением 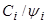 на рис. 4. Из рис. 4 видно, что профиль концентрации также существенно зависит от параметра
на рис. 4. Из рис. 4 видно, что профиль концентрации также существенно зависит от параметра 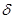 . По рис. 2 и 4 можно отметить, что при
. По рис. 2 и 4 можно отметить, что при 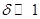 у стенки с более высокой температурой концентрация компонентов выше и также выше скорость конвективного потока. При
у стенки с более высокой температурой концентрация компонентов выше и также выше скорость конвективного потока. При 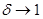 профиль концентрации сходится к профилю для плоского слоя (на рис. 4 показан штриховой линией).
профиль концентрации сходится к профилю для плоского слоя (на рис. 4 показан штриховой линией).
Рис. 4. Профиль концентрации  компонента смеси в поперечном сечении
компонента смеси в поперечном сечении 
при различных 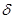 . Штриховая линия соответствует профилю для плоской колонны
. Штриховая линия соответствует профилю для плоской колонны
Если изменения плотности, связанные с неоднородностью концентрации, учитывается, то решение задачи (13), (14) принимает более сложный вид и зависит от значения суммарного отношения разделения 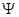 . Этот случай будет исследован в дальнейшем.
. Этот случай будет исследован в дальнейшем.
Заключение
В данной работе приведено теоретическое исследование процесса разделения многокомпонентной смеси в цилиндрической термодиффузионной колонне, на стенках которой поддерживаются различные постоянные температуры. Исследование выполнено в цилиндрических координатах с целью учета влияния кривизны и отношения радиусов цилиндров на процесс разделения. Построены точные решения задачи, имеющие различный вид в зависимости от значения управляющих параметров. Также рассмотрен случай, при котором влиянием неоднородности плотности, вызванной изменением концентрации смеси, на конвективное течение смеси можно пренебречь.
На основании полученных результатов можно сделать вывод, что поля физических характеристик существенно зависят от отношения радиусов 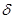 . При
. При 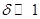 температура, скорость конвективного течения и концентрация компонентов смеси выше у внутренней стенки, где смесь движется вверх. При
температура, скорость конвективного течения и концентрация компонентов смеси выше у внутренней стенки, где смесь движется вверх. При  результаты представленных в данной работе решений задачи согласуются с результатами для плоской колонны.
результаты представленных в данной работе решений задачи согласуются с результатами для плоской колонны.
Исследование проведено под руководством д.ф.-м.н. И.И. Рыжкова (Институт вычислительного моделирования СО РАН, г. Красноярск).
Работа выполнена при поддержке гранта РФФИ №15–01–03293–а.
Литература:
1. Wiegand S. Thermal diffusion in liquid mixtures and polymer solutions. Journal of Physics: Condensed Matter, 2004. – V. 16. – P. 357–379.
2. Firoozabadi A. Thermodynamics of hydrocarbon reservoirs. McGraw–Hill Professional, 1999.
3. Рабинович Г.Д. Разделение изотопов и других смесей термодиффузией. – М.: Атомиздат, 1981. – 144 c.
4. Platten J.K. The Soret effect: A review of recent experimental results. Journal of Applied Mechanics, 2006. – V. 73. Р. 5–15.
5. Рыжков И.И. Термодиффузия в смесях: уравнения, симметрии, решения и их устойчивость. Новосибирск: Издательство СО РАН, 2013. – 200 с.
6. Ryzhkov I.I. and Shevtsova V.M. On thermal diffusion and convection in multicomponent mixtures with application to the thermogravitational column. Physics of Fluids, 2007. – V. 19. Issue 2, 027101.
7. Ryzhkov I.I. and Shevtsova V.M. Convective stability of multicomponent fluids in the thermogravitational column. Physical Review E, 2009. – V. 79. Issue 2, 026308.
8. Bou–Ali M.M., Ecenarro O., Madariaga J.A., Santamaria C.M. Stability of convection in a vertical binary fluid layer with an adverse density gradient. Phys. Rev. E, 1999. – V. 59, No.~1. – P. 1250–1252.
9. Bou–Ali M.M., Ecenarro O., Madariaga J.A., Santamaria C.M. Measurement of negative Soret coefficients in a vertical fluid layer with an adverse density gradient. Phys. Rev. E, 2000. – V. 62, No. 1. – P. 1420–1423.
10. Valencia J., Bou–Ali M.M., Ecenarro O., Madariaga J.A., Santamaria C.M. Validity limits of the FJO thermogravitational column theory. Lect. Notes Phys, 2002. – V. 584. – P. 233–249.







