Статья посвящена моделированию процессов формирования устойчивых во времени образований (структур), состоящих из магнитных частиц (диполей). В работе полностью описана математическая модель и представлены результаты одного из вычислительных экспериментов.
Ключевые слова: диполь, ферромагнетик, магнитная частица, однодоменная частица, устойчивые образования.
Введение
Большой интерес в науке представляет собой поиск и обоснование устойчивых во времени образований из магнитных частиц (диполей), полученных под действием сил взаимодействия с учетом внешнего магнитного поля [1]. Например, на сегодняшний день с большой достоверностью установлено наличие магнитных материалов в выпадающих микрочастицах импактных космических тел [2]. Во время полета в атмосфере при абляции вещества с поверхности тела срываются перегретые частицы, содержащие железо, его соединения и окислы, которые являются ферромагнетиками [2]. Также имеет место явление остаточной термонамагниченности, которая образуется при остывании материала в геомагнитном поле, начиная с некоторой температуры выше точки Кюри. Ее рост при снижении температуры идет довольно интенсивно, но при остывании до «блокирующей» температуры резко замедляется и происходит «замораживание» приобретенной намагниченности [3]. Термонамагниченность может в десятки и сотни раз превышать намагниченность, возникающую в том же поле при комнатной температуре. Для ее разрушения требуются магнитные поля, в десятки и сотни раз превышающие создавшее ее поле. Итак, в результате абляции и взрывов идет образование микрочастиц с содержанием железа и его окислов. В результате снижения частиц в атмосфере железо и его сплавы хоть и окисляются, но вновь порождают ферромагнитные соединения. При остывании ниже точки Кюри эти частицы приобретают сильный магнитный момент. Так удельный магнитный момент может быть огромным у однодоменных частиц или вкраплений, насчитывающих несколько десятков тысяч молекул.
С целью изучения эффектов, возникающих при формировании устойчивых во времени структур, состоящих из диполей, рассмотрена задача численного моделирования взаимодействия дипольных частиц, обладающих большим по сравнению с внешним магнитным полем дипольным моментом.
Математическая модель
В качестве магнитной частицы рассмотрим сферу с равномерным распределением плотности. Будем считать, что вектор дипольного момента 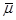 частицы проходит через центр сферы.
частицы проходит через центр сферы.
Для описания движения частиц введем инерциальную [4] декартову систему координат 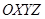 . Движение каждой частицы представим в виде суперпозиции поступательного и вращательного движений [5]. Поступательное движение определим перемещением центром масс, а вращательное – вокруг центра масс. Для описания поступательного движения частицы выпишем силу, действующую на ее центр масс, и используем второй закон Ньютона. Вращательное движение смоделируем под действием вращательного момента, который определим относительно центра масс. Для описания вращательного движения каждой
. Движение каждой частицы представим в виде суперпозиции поступательного и вращательного движений [5]. Поступательное движение определим перемещением центром масс, а вращательное – вокруг центра масс. Для описания поступательного движения частицы выпишем силу, действующую на ее центр масс, и используем второй закон Ньютона. Вращательное движение смоделируем под действием вращательного момента, который определим относительно центра масс. Для описания вращательного движения каждой 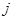 -той частицы сопоставим ей локальную подвижную систему координат
-той частицы сопоставим ей локальную подвижную систему координат 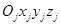 , жестко закрепленную с частицей. Таким образом, вращение каждой частицы отождествим с вращением соответствующей подвижной системы координат. Описание вращения подвижной системы координат
, жестко закрепленную с частицей. Таким образом, вращение каждой частицы отождествим с вращением соответствующей подвижной системы координат. Описание вращения подвижной системы координат 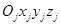 осуществим с помощью углов Эйлера
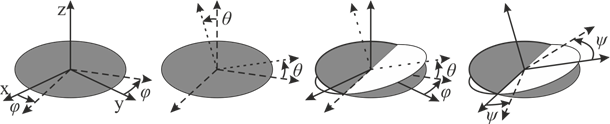
осуществим с помощью углов Эйлера 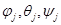 [4], интерпретация которых изображена на рис. 1.
[4], интерпретация которых изображена на рис. 1.
|
|
|
Рис. 1. Углы Эйлера |
Постановка задачи
Рассмотрим 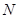 частиц. Для каждой из них на момент времени
частиц. Для каждой из них на момент времени 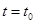 в инерциальной декартовой системе координат
в инерциальной декартовой системе координат 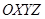 определим следующие величины:
определим следующие величины:
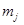 – масса;
– масса;
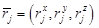 – радиус-вектор центра масс частицы;
– радиус-вектор центра масс частицы;
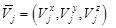 – вектор поступательной скорости центра масс;
– вектор поступательной скорости центра масс;
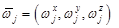 – вектор угловой скорости относительно центра масс;
– вектор угловой скорости относительно центра масс;
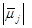 – модуль вектора дипольного момента;
– модуль вектора дипольного момента;
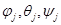 – углы Эйлера.
– углы Эйлера.
Кроме того, для каждой 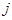 -той частицы
-той частицы 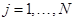 в соответствующей локальной системе координат
в соответствующей локальной системе координат 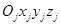 , привязанной к главным центральным осям тензора инерции, зададим
, привязанной к главным центральным осям тензора инерции, зададим
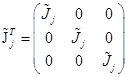 , – тензор инерции;
, – тензор инерции;
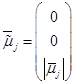 . – вектор дипольного момента.
. – вектор дипольного момента.
Здесь и далее символ «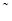 » означает, что величина задана в подвижной системе координат.
» означает, что величина задана в подвижной системе координат.
Требуется для каждой 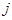 -ой частицы
-ой частицы 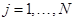 определить на момент времени
определить на момент времени 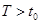 значения следующих величин:
значения следующих величин: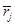 ,
, 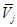 ,
, 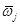 ,
, 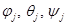 .
.
Уравнения движения
Взаимодействие дипольных частиц осуществляется посредством поля, порожденного всеми диполями и внешним полем. Напряженность полного поля, действующего на 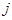 -тую частицу, описывается формулой
-тую частицу, описывается формулой
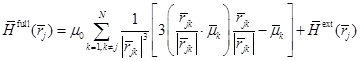 , (1)
, (1)
где 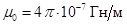 – магнитная проницаемость вакуума,
– магнитная проницаемость вакуума, 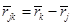 ,
, 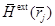 – внешнее магнитное поле, действующее на
– внешнее магнитное поле, действующее на 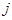 -тую частицу. Функция
-тую частицу. Функция 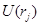 потенциальной энергии взаимодействия
потенциальной энергии взаимодействия 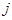 -той молекулы с полным полем определяется формулой
-той молекулы с полным полем определяется формулой
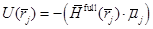 . (2)
. (2)
Известно, что сила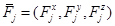 , действующая на центр масс
, действующая на центр масс 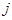 -той частицы, представима в виде
-той частицы, представима в виде
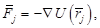 (3)
(3)
где символ «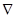 » означает оператор градиента:
» означает оператор градиента: 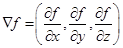 . В качестве дифференциального уравнения, описывающего поступательное движение
. В качестве дифференциального уравнения, описывающего поступательное движение 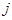 -той частицы, используем второй закон Ньютона:
-той частицы, используем второй закон Ньютона:
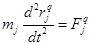 ,
, 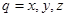 ;
; 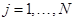 . (4)
. (4)
Уравнение (4) сведем к системе обыкновенного дифференциального уравнения (ОДУ) первого порядка посредством использования компонент вектора скорости:
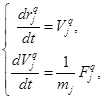
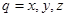 ;
; 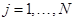 . (5)
. (5)
После проведения не сложных преобразований, с учетом (1)–(5), получим
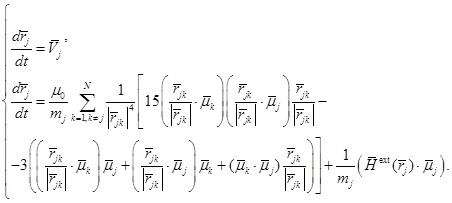 (6)
(6)
Уравнения (6) формируют систему ОДУ первого порядка, состоящую из скалярных уравнений.
Вращательное движение 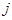 -той частицы опишем вращением частицы вокруг ее центра масс под действием момента сил
-той частицы опишем вращением частицы вокруг ее центра масс под действием момента сил 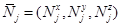 , который определяется равенством
, который определяется равенством
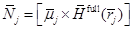 ,
, 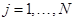 , (7)
, (7)
где символ «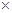 » означает векторное произведение двух векторов. Например, для двух векторов
» означает векторное произведение двух векторов. Например, для двух векторов 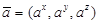 и
и 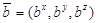 имеет мест равенство
имеет мест равенство
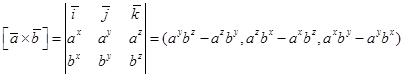 .
.
Для описания вращательного движения каждой 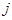 -ой частицы сопоставим ей локальную подвижную систему координат
-ой частицы сопоставим ей локальную подвижную систему координат 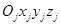 , жестко закрепленную с частицей. Таким образом вращение каждой
, жестко закрепленную с частицей. Таким образом вращение каждой 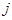 -ой частицы отождествим с вращением
-ой частицы отождествим с вращением 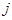 -ой подвижной системы координат. Описание вращения подвижной системы координат
-ой подвижной системы координат. Описание вращения подвижной системы координат 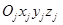 осуществим с помощью углов Эйлера
осуществим с помощью углов Эйлера 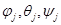 [4]. Углы
[4]. Углы 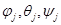 называются углами прецессии, нутации и собственного вращения соответственно. Исходя из определения углов Эйлера, построена [6] матрица
называются углами прецессии, нутации и собственного вращения соответственно. Исходя из определения углов Эйлера, построена [6] матрица 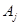 перехода от подвижной системы координат
перехода от подвижной системы координат 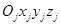 к инерциальной системе
к инерциальной системе 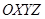
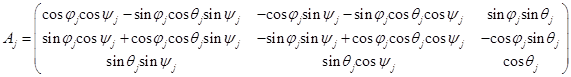 .
.
Итак, зная координаты вектор-столбца 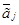 в подвижной системе координат
в подвижной системе координат 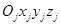 , мы можем вычислить координаты этого вектора
, мы можем вычислить координаты этого вектора 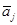 в инерциальной системе
в инерциальной системе 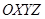 по формуле
по формуле 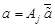 . Аналогично построена матрица
. Аналогично построена матрица 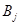 перехода от инерциальной системы координат к подвижной системе
перехода от инерциальной системы координат к подвижной системе
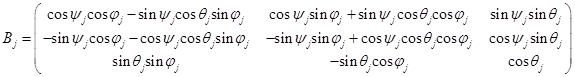 .
.
Вращательное движение каждой 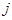 -ой частицы опишем дифференциальным уравнением моментов, которое в подвижной системе координат
-ой частицы опишем дифференциальным уравнением моментов, которое в подвижной системе координат 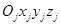 имеет вид
имеет вид
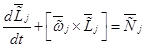 ,
, 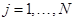 . (8)
. (8)
Здесь 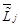 – момент импульса
– момент импульса 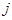 -ой частицы, который определяется в виде
-ой частицы, который определяется в виде
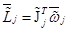 ,
, 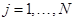 . (9)
. (9)
Поскольку все диагональные элементы тензора инерции 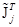 равны между собой, то
равны между собой, то
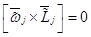 ,
, 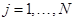 . (10)
. (10)
Так как каждая 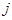 -тая частица жестко закреплена с соответствующей подвижной системой координат
-тая частица жестко закреплена с соответствующей подвижной системой координат 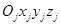 , то элементы тензора инертности не меняются со временем
, то элементы тензора инертности не меняются со временем
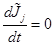 ,
, 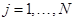 . (11)
. (11)
С учетом (9)–(11) уравнение моментов (8) сводится к системе ОДУ:
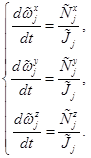
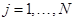 . (12)
. (12)
Уравнения (12) характеризуют изменения во времени угловой скорости 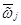 , заданной в подвижной системе координат
, заданной в подвижной системе координат 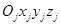 . Определим, как изменяется во времени сама подвижная система координат. Для этого выпишем уравнения, характеризующие связь между производной по времени от углов Эйлера
. Определим, как изменяется во времени сама подвижная система координат. Для этого выпишем уравнения, характеризующие связь между производной по времени от углов Эйлера 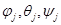 и угловой скоростью
и угловой скоростью 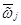 [6]
[6]
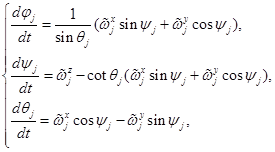
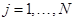 . (13)
. (13)
Интегрирование системы (12)–(13), содержащей в себе 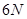 скалярных уравнений, в общем случае может быть выполнено только численно.
скалярных уравнений, в общем случае может быть выполнено только численно.
Начальные данные
Пусть вычислительная область – сфера диаметра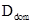 . В качестве диполей рассмотрим однодоменные [7] частицы железа шарообразной формы. Показано [8], что радиус таких частиц может достигать значения 1.4 ∙
. В качестве диполей рассмотрим однодоменные [7] частицы железа шарообразной формы. Показано [8], что радиус таких частиц может достигать значения 1.4 ∙ 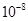 метра. Для частиц максимального радиуса с приемлемой для нас степенью точности известны [2] их физические параметры:
метра. Для частиц максимального радиуса с приемлемой для нас степенью точности известны [2] их физические параметры:
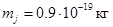 ;
; 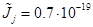 кг.м2;
кг.м2; 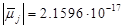 А.м2. (14)
А.м2. (14)
На начальный момент времени 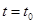 поступательную и угловую скорости каждой частицы определим равными нулю
поступательную и угловую скорости каждой частицы определим равными нулю
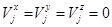 ;
; 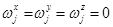 . (15)
. (15)
Углы Эйлера 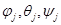 и координаты радиус-вектора
и координаты радиус-вектора 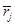 будем задавать различными способами с учетом следующих ограничений:
будем задавать различными способами с учетом следующих ограничений:
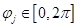 ;
; 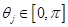 ,
, 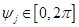 ,
, 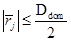 . (16)
. (16)
Минимально допустимым расстоянием 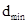 между центрами масс магнитных частиц определим равным трем диаметрам частицы:
между центрами масс магнитных частиц определим равным трем диаметрам частицы:
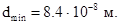 (17)
(17)
Компьютерная арифметика использует ограниченную запись вещественных чисел. Для традиционных языков программирования максимальная точность представления вещественного числа составляет 15 значащих цифр. Поэтому для корректных вычислений желательно, чтобы отношение максимального числа к минимальному по модулю числу не превышало 1015. Исходя из этого ограничения в [9] показано, что диаметр 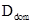 вычислительной области следует задать в следующем виде:
вычислительной области следует задать в следующем виде:
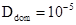 м. (18)
м. (18)
Проведем масштабирование единиц измерения [10] с параметрами указанными в [9]:
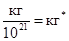 ,
, 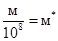 ,
, 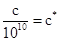 ,
, 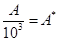 .
.
Тогда, с учетом (17) вместо (14)–(17) получим следующие значения:
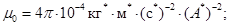
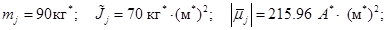 (19)
(19)
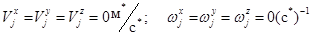
и ограничения
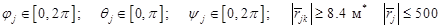 . (20)
. (20)
В качестве начальных данных используем значения (19) и ограничения (20).
Численное решение
Для поиска численного решения системы ОДУ, состоящей из уравнений (6), (12)–(13), использовались три различных метода первого, второго и четвертого порядков точности из семейства явных численных методов типа Рунге-Кутты [11] с контролем точности и устойчивости.
Алгоритм поиска численного решения
Таким образом, для численного моделирования процессов формирования устойчивых образований из частиц с магнитным дипольным моментом был реализован следующий алгоритм:
1) Зададим значение времени 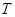 и первый шаг по времени
и первый шаг по времени 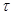 ;
;
2) Определим число дипольных частиц 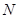 и для каждой из них зададим начальные данные в соответствии с (19), (20);
и для каждой из них зададим начальные данные в соответствии с (19), (20);
3) Запустим цикл по времени. На каждом шаге по времени выполним следующие действия:
I. Вычислим векторы 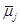 ,
, 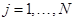 по формуле
по формуле 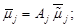
II. Определим силы 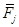 ,
, 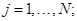
III. По формуле (1) рассчитаем полное магнитное поле 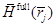 , действующее на
, действующее на 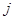 -тую частицу,
-тую частицу,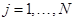 ;
;
IV. Вычислим по формуле (7) значение вращательного момента сил 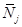 , действующего на
, действующего на 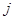 -тую частицу,
-тую частицу, 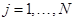 , в инерциальной системе координат
, в инерциальной системе координат 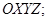
V. Рассчитаем по формуле 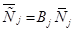 ,
, 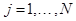 , вращательный момент сил
, вращательный момент сил 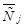 в соответствующей локальной системе координат
в соответствующей локальной системе координат 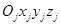 ;
;
VI. Определим по формуле 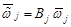 ,
, 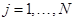 , угловую скорость
, угловую скорость 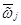 в соответствующей локальной системе координат
в соответствующей локальной системе координат 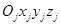 ;
;
VII. Сформируем системы ОДУ по формулам (6), (12), (13) и найдем ее решение численным методом;
VIII. Выполним обновление переменных, значение которых меняется при переходе на следующий слой по времени;
IX. Пересчитаем по формуле 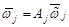 ,
, 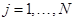 , новое значение угловой скорости
, новое значение угловой скорости 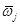 в инерциальной системе координат
в инерциальной системе координат 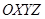 ;
;
X. Окончим моделирование или перейдем к пункту I цикла по времени.
Вычислительный эксперимент
Изначально была проведена апробация и сравнение численных методов решения систем ОДУ на тестовых задачах. Наиболее точные расчеты за меньшее время вычислений получены с помощью метода Мерсона [12] четвертого порядка точности. Кроме этого был проведен ряд расчетов для тестирования всей программы. В частности, был смоделирован эффект, наблюдаемый при взаимодействии ферромагнитных частиц, разбросанных на листе бумаги, с полем постоянного магнита. Как известно [13], хаотически ориентированные частицы под действием внешнего поля выстраиваются вдоль линий напряженности внешнего поля (рис. 2).
Один из вычислительных экспериментов состоял в следующем. Расположим дипольные частицы под углом 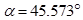 к плоскости
к плоскости 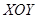 , а направление их дипольных моментов зададим случайным образом. Под действием слабого внешнего магнитного поля
, а направление их дипольных моментов зададим случайным образом. Под действием слабого внешнего магнитного поля
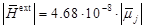 ,
,
направленного противоположно оси OZ, магнитные частицы упорядочиваются вдоль линий напряженности внешнего поля (рис. 3).

Рис. 2. Взаимодействие металлических ферромагнитных частиц с полем постоянного магнита
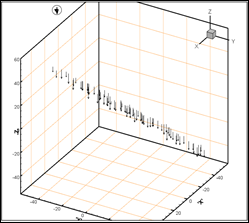
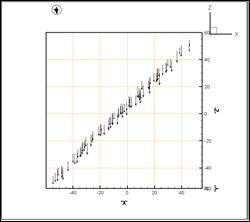
Рис. 3. Начальное положение частиц: слева – вид в пространстве,
справа – вид в проекции на плоскость ZOX
Однако с течением времени дипольные моменты частиц меняют своё направление (рис. 4). В результате взаимодействия между собой и с внешним полем дипольные моменты частиц ориентируются вдоль направления их расположения в пространстве и принимают устойчивое во времени состояние (рис. 5).
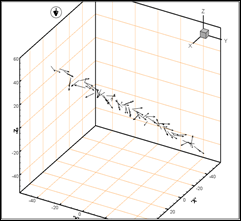
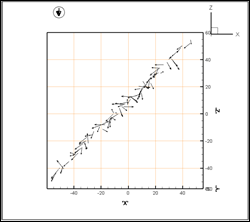
Рис. 4. Положения частиц в момент поиска устойчивого состояния:
слева – вид в пространстве, справа – вид в проекции на плоскость ZOX
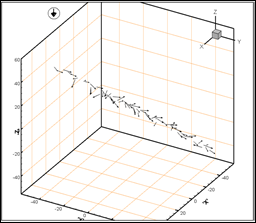
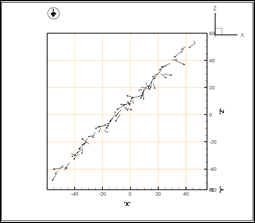
Рис. 5. Устойчивое положение частиц: слева – вид в пространстве,
справа – вид в проекции на плоскость ZOX
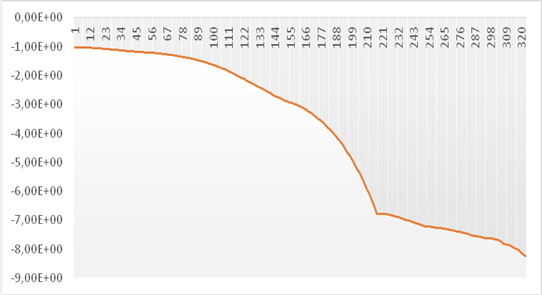
На рис. 6 по оси абсцисс отмечен номер шага по времени, а по оси ординат выписано значение функции потенциальной энергии системы частиц, вычисленной по формуле
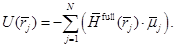
Как видно из рис. 6, потенциальная энергия системы уменьшается пока не достигнет своего минимального значения, соответствующего устойчивому состоянию, показанному на рис. 5.
Таким образом продемонстрировано, что под действием слабого внешнего поля магнитные частицы ориентируются вдоль линий напряженности внешнего поля, тем самым создавая огромный дипольный момент и формируя в пространстве устойчивые во времени образования.
|
|
|
Рис. 6. Изменение потенциальной энергии системы частиц |
Заключение
В рамках статьи полностью описана математическая модель взаимодействия магнитных дипольных частиц между собой и с внешним полем. Вращение дипольных частиц в пространстве осуществлено под действием момента сил. Представлен пошаговый алгоритм, который лег в основу создания комплекса программ для изучения процессов формирования устойчивых образований из диполей. В качестве диполей рассмотрена однодоменные частицы железа шарообразной формы с реальными физическими параметрами. Проведена верификация созданного программного комплекса. Посредством вычислительного эксперимента показано, что магнитные частицы, находясь под действием слабого внешнего однородного поля, формируют большой дипольный момент и ориентируются вдоль созданного ими поля, принимая устойчивое во времени состояние.
Работа выполнена в рамках Проекта РНФ № 14-01-00147.
Литература:
1. Маттис Д. Теория магнетизма / Д. Маттис. – М.: Мир, 1967.
2. Краткий справочник по химии / ред. О.Д. Куриленко. – 4-е изд., исправл. и доп. – Киев: Наукова думка, 1974. – 992 с.
3. Яновский Б.М. Земной магнетизм / Б.М. Яновский. – M.: МГУ, 1978.
4. Ландау Л.Д. Теоретическая физика в 10 т. Т. 1: Механика. Электродинамика / Л.Д. Ландау, Е.М. Лифшиц. – 3-е изд., перераб. и доп. – М.: Наука, 1973. – 208 с.
5. Киттель Ч. Введение в физику твердого тела / Ч. Китель. – М.: Наука, 1978. – 791 с.
6. Поляхов Н.Н. Теоретическая механика / Н.Н. Поляхов, С.А. Зегжда, М.П. Юшков; под ред. проф. Н.Н.Поляхова. – Л.: изд-во Ленингр. ун-та, 1985. – 536 с.
7. Вонсовский С.В. Магнетизм / С.В. Вонсовский. – М.: Из-во физ.-мат. лит., 1971. – 1032 с.
8. Чернавский П.А. Новое в магнитных методах исследования металлнанесенных каталиаторов / П.А. Чернавский // Рос. хим. ж. (Ж. Рос. хим. об-ва. им. Д.И. Менделеева). – 2002. – Т. XLVI, №3. – С. 19–30.
9. Вяткин А.В. Численная аппроксимация поля в задаче взаимодействия дипольных частиц: дис. канд. физ.-мат. наук / Bяткин A.B. – Красноярск, 2010. – 132 с.
10. Лабутин А.А. Краткие сведения о международной системе единиц измерений (СИ) / А.А. Лабутин. – Киев: Вища школа, 1975. – 88 с.
11. Бахвалов Н.С. Численные методы / Н.С. Бахвалов. – М.: Наука, 1975.
12. Захаров А.Ю. Некоторые результаты сравнений эффективности методов решения систем обыкновенных дифференциальных уравнений: Препринт № 125 / А.Ю. Захаров. – М.: Изд. ИПМ АН СССР, 1979. – 25 с.
13. Боровик Е.С. Лекции по магнетизму / Е.С. Боровик, В.В. Еременко, А.С. Мильнер. – 3-е изд., перераб. и доп. – М.: ФИЗМАТЛИТ, 2005. – 512 с.