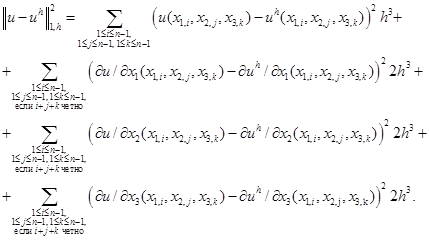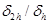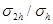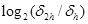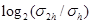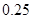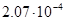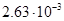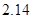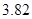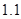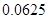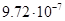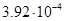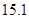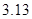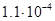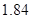Введение
При численном решении уравнений математической физики методом конечных элементов лагранжевы элементы используются значительно чаще, чем эрмитовы элементы. Однако в ряде случаев эрмитовы элементы обладают некоторыми преимуществами перед лагранжевыми. В статье [1] проведено сравнение применения некоторых лагранжевых и эрмитовых конечных элементов одинаковых степеней. Показано, что для достижения сходимости одинакового порядка размерность системы уравнений метода конечных элементов для эрмитовых элементов ощутимо меньше, чем при использовании лагранжевых элементов. Особенно существенной эта разница становится в трехмерном случае.
В литературе по методу конечных элементов описание эрмитовых элементов начинается с бикубических элементов. Между тем, в предположении бо́льшей эффективности интерес представляют также эрмитовы элементы меньшей степени. В статье [2] впервые представлены биквадратные эрмитовы элементы и численно подтвержден их теоретический порядок точности, а также установлен повышенный порядок точности сходимости производных. В статье [1] продолжено их теоретическое исследование и тоже представлены результаты численных экспериментов. Кроме того, для решения трехмерных задач предложены триквадратные элементы. В данной работе для них изложена теоретическая оценка сходимости и приведены результаты численного решения краевой задачи для уравнения Пуассона в единичном кубе, полученного методом конечных элементов с использованием этих элементов.
Триквадратные эрмитовы элементы на кубе
Определим «эталонный» триквадратный эрмитов элемент как тройку [3]
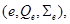
где 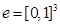 – единичный куб в пространстве
– единичный куб в пространстве 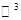 с вершинами
с вершинами 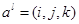 ,
, 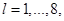
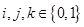 , которые являются узлами элемента;
, которые являются узлами элемента; 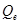 – пространство полиномов вида
– пространство полиномов вида
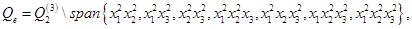
(здесь 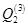 – пространство полиномов степени не выше 2 по каждой переменной);
– пространство полиномов степени не выше 2 по каждой переменной); 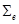 – множество степеней свободы (рис. 1)
– множество степеней свободы (рис. 1)
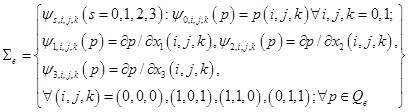 .
.
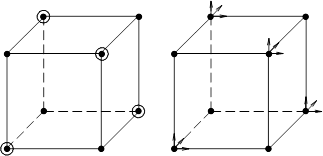
a) b)
Рис. 1. Схематическое обозначение степеней свободы.
В общепринятой классификации жирные точки в узлах означают задание значения
функции, а кружки в варианте a) – задание всех (трех) первых производных. В варианте b) эти же степени свободы изображены стрелками в соответствующих направлениях
Справедливо следующее утверждение [1].
Лемма 1. Тройка 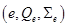 определяет корректный конечный элемент с унисольвентной парой
определяет корректный конечный элемент с унисольвентной парой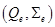 .
.
Обоснование Леммы осуществлялось прямым построением базиса Лагранжа. Напомним [3], что функции
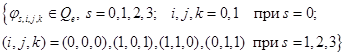
образуют базис Лагранжа в пространстве 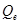 относительно множества степеней свободы
относительно множества степеней свободы 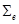 , если они удовлетворяют условию
, если они удовлетворяют условию
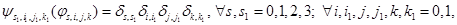
где 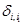 – символ Кронекера.
– символ Кронекера.
Непосредственная проверка показывает, что базис Лагранжа имеет следующий вид [1]:
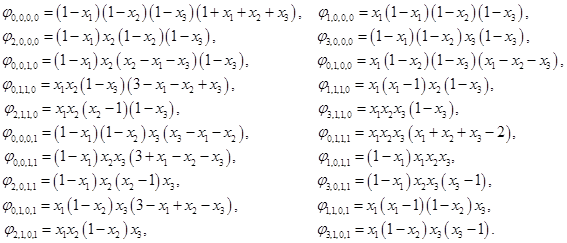
Введем обозначения для норм, которые мы будем использовать при оценке сходимости. Пусть 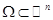 . Обозначим через
. Обозначим через 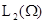 пространство функций, определённых и измеримых на
пространство функций, определённых и измеримых на 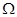 со скалярным произведением
со скалярным произведением
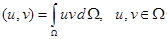
и конечной нормой
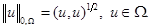
Для частных производных порядка 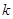 введем полунорму
введем полунорму
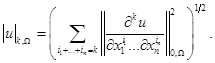
Через 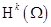 обозначим пространство функций, определенных и измеримых на
обозначим пространство функций, определенных и измеримых на 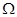 вместе с производными до порядка
вместе с производными до порядка 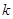 включительно, с конечной нормой [4]
включительно, с конечной нормой [4]
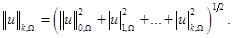
Пусть 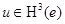 . По теореме вложения Соболева
. По теореме вложения Соболева 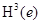 непрерывно вложено в
непрерывно вложено в 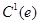 [4]. Поэтому для функции
[4]. Поэтому для функции 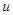 мы можем определить ее интерполянт
мы можем определить ее интерполянт 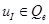 . Введем обозначение
. Введем обозначение 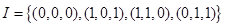 для множества узлов, в которых степени свободы содержат производные. Тогда
для множества узлов, в которых степени свободы содержат производные. Тогда
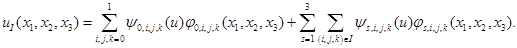
Теорема 1. Пусть 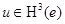 . Тогда для любого
. Тогда для любого 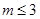
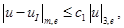
где константа 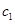 не зависит от функции
не зависит от функции 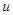 .
.
Доказательство. Как отмечено выше, пространство 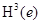 непрерывно вложено в
непрерывно вложено в 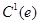 . Кроме того, пространство
. Кроме того, пространство 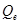 содержит пространство полиномов полной степени не выше 2, определенных на
содержит пространство полиномов полной степени не выше 2, определенных на 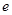 . Таким образом, выполнены все условия теоремы 1 [2, глава 3, параграф 10], откуда следует оценка (4).
. Таким образом, выполнены все условия теоремы 1 [2, глава 3, параграф 10], откуда следует оценка (4). 
Численное решение уравнения Пуассона
В области 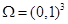 с границей
с границей 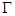 рассмотрим следующую задачу:
рассмотрим следующую задачу:
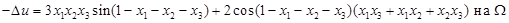
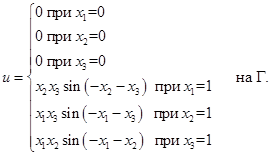
Ей соответствует точное решение
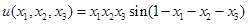 .
.
Построим на 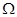 равномерную триангуляцию, поделив
равномерную триангуляцию, поделив 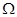 на
на 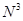 одинаковых кубиков-ячеек меньшего размера. Для этого проведем плоскости
одинаковых кубиков-ячеек меньшего размера. Для этого проведем плоскости
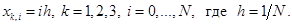
На каждую элементарную ячейку 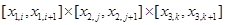 отобразим «эталонный» элемент одним из двух аффинных отображений
отобразим «эталонный» элемент одним из двух аффинных отображений
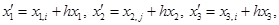
когда величина 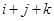 принимает четное значение, либо
принимает четное значение, либо
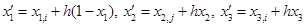
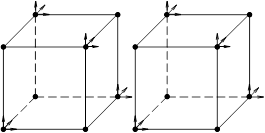
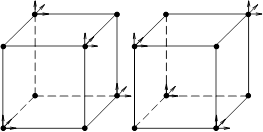
в остальных случаях. В нашем случае обойтись одним преобразованием (7) нельзя. Дело в том, что при использовании только одного отображения (7) для соседних элементов, имеющих один или несколько общих узлов, число степеней свободы в этих узлах может не совпадать (см. рис. 2 a)). Чтобы избежать этого, отображения (7) и (8) чередуются на соседних ячейках. Например, если элемент является образом «эталонного» элемента (1)–(3), полученным отображением (7), то все соседние элементы, имеющие с ним общие грани, должны быть получены отображением (8). В этом случае степени свободы у соседних элементов совпадают во всех узлах триангуляции. Пример двух соседних элементов, полученных с использованием разных отображений, показан на рис. 2 b). Базисные функции каждого элемента являются образами базисных функций «эталонного» элемента при соответствующем аффинном отображении.
a) b)
Рис. 2. a) – неправильное примыкание двух ячеек, b) – правильное примыкание
Теперь обсудим альтернативу с заданием некоторых граничных значений. Для этого обратимся к рис. 3. Дело в том, что некоторые степени свободы, например, производные в начале координат, можно вычислить непосредственно из краевых условий. А в принципе, можно оставить их неизвестными и попытаться найти в ходе решения всей задачи в целом. В общем, второй вариант может незначительно увеличить число неизвестных, но облегчить подготовку данных. Однако второй вариант оказался полностью неприменимым. В этом случае происходит нарушение главных краевых условий в пространстве тестовых функций, что выливается в дополнительную погрешность приближенного решения, ухудшающую порядок сходимости. Это отчетливо проявляется в вычислительных экспериментах. Таким образом, степени свободы – первые производные, которые могут быть вычислены из известных краевых условий, должны быть заданы явно. И это несмотря на то, что решается краевая задача Дирихле, в которой заданы только значения функции на границе области.
|
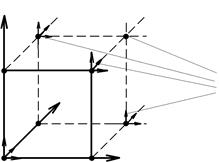
Рис. 3. Угол области решения. Жирными точками и стрелками в узлах триангуляции
помечены степени свободы конечных элементов. Лишь четыре степени свободы
из изображенных здесь являются неизвестными. Остальные вычисляются
непосредственно из известных граничных значений решения и не порождают неизвестных
Чтобы оценить порядок точности приближенного решения, сравним значения погрешности при различных значениях шага 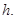 Построим систему алгебраических уравнений метода конечных элементов, используя триквадратные эрмитовы элементы для
Построим систему алгебраических уравнений метода конечных элементов, используя триквадратные эрмитовы элементы для 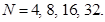 Зная точное решение, можно вычислить значение погрешности
Зная точное решение, можно вычислить значение погрешности 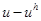 , где
, где 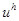 – приближенное решение. Мы будем использовать дискретные нормы
– приближенное решение. Мы будем использовать дискретные нормы
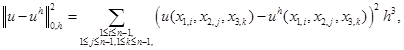
Заметим, что значения производных во второй норме совпадают со значениями степеней свободы и поэтому не требуют дополнительных вычислений.
Для решения из 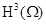 мы имеем следующие теоретические оценки.
мы имеем следующие теоретические оценки.
Теорема 2. Пусть 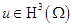 . Тогда справедливы следующие оценки:
. Тогда справедливы следующие оценки:
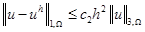
и
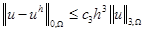
с константами 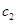 и
и 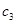 , независящими от
, независящими от 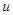 и
и 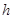 .
.
Доказательство. Оценка (11) получается стандартным способом из оценки (4) с учетом вида отображения (7),(8) [3, 4]. Оценка (12) следует из (11) с использованием приема Нитше [3, 4]. 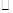
Таким образом, теоретически для решения задачи (5),(6) мы имеем сходимость второго порядка в норме 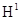 и третьего порядка в норме
и третьего порядка в норме 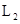 .
.
В таблице 1 приведены значения нормы погрешности 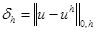 и
и 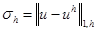 для разных значений шага
для разных значений шага 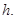 Анализ полученных результатов показывает, что при уменьшении
Анализ полученных результатов показывает, что при уменьшении 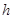 величина
величина 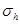 стремится ко второму порядку точности, как и соответствующая теоретическая оценка (11). Что касается величины
стремится ко второму порядку точности, как и соответствующая теоретическая оценка (11). Что касается величины 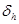 , характеризующей погрешность в норме
, характеризующей погрешность в норме 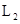 , то здесь, как и в двумерном случае [1], ее порядок выше, чем в теоретической оценке (12). При малых значениях
, то здесь, как и в двумерном случае [1], ее порядок выше, чем в теоретической оценке (12). При малых значениях 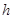 он близок к 4. Мы полагаем, что это можно объяснить следующим образом. На равномерной сетке мы получаем конечно-разностную схему с симметричным шаблоном. Такая схема не позволяет получить нечетный порядок аппроксимации, поскольку при разложении в ряд Тейлора, слагаемые нечетной степени сокращаются. В результате после сокращения слагаемых третьего порядка точности остаются только слагаемые четвертого порядка. Именно они обеспечивают четвертый порядок сходимости для дискретного набора значений.
он близок к 4. Мы полагаем, что это можно объяснить следующим образом. На равномерной сетке мы получаем конечно-разностную схему с симметричным шаблоном. Такая схема не позволяет получить нечетный порядок аппроксимации, поскольку при разложении в ряд Тейлора, слагаемые нечетной степени сокращаются. В результате после сокращения слагаемых третьего порядка точности остаются только слагаемые четвертого порядка. Именно они обеспечивают четвертый порядок сходимости для дискретного набора значений.
Таблица 1
Точность приближенного решения
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Заключение
Итак, в этой работе продолжено изложение свойств эрмитовых триквадратных конечных элементов. Теоретические оценки сходимости подтверждены результатами проведенных численных экспериментов. Более того, как и в случае биквадратных конечных элементов, на равномерной сетке получен повышенный порядок точности в дискретной среднеквадратичной норме. На основании представленных результатов мы полагаем, что триквадратные конечные элементы могут быть эффективно использованы при аппроксимации функций из 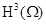 .
.
Работа поддержана грантом РФФИ № 14-01-00224.
Литература:
1. Shaidurov V., Shut S., Gileva L. Some properties of Hermite finite elements on rectangles, AIP Conference Proceedings 1629, 32(2014). – Pp. 32–43.
2. Шайдуров В.В., Шуть С.В. Применение эрмитового биквадратного конечного элемента // Вестник СибГАУ, 2014. – № 2. – С. 80–85.
3. Сьярле Ф. Метод конечных элементов для эллиптических задач. – Москва, Мир, 1980. – 512 с.
4. Даутов Р.З., Карчевский М.М. Введение в теорию метода конечных элементов. – Казань, Казанский университет, 2011. – 240 с.
5. Adams R.A., Fournier J.J.F. Sobolev Spaces. Academic Press. – New York, 2003.