В этой работе дается ряд примеров, изложение которых подчеркивает значимость теоремы Вейерштрасса о пределе последовательности.
Как известно, уравнения типа
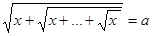, (1)
где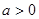 
— некоторое вещественное число, решаются следующим образом: возведя в квадрат обе части равенства (1), получим
.
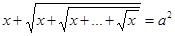Так как второе слагаемое совпадает с левой частью исходного уравнения, то
.
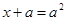Отсюда, находим единственное решение уравнения (1):
.
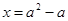Пользуясь некоторыми понятиями начал анализа, решим уравнение (1) иным способом. Для этого, сначала, рассмотрим последовательность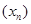 
, где
.
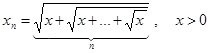Докажем, что последовательность 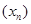монотонна и ограничена. В курсе алгебры и начал анализа учащиеся знакомятся с теоремой Вейерштрасса: если последовательность монотонна и ограничена, то она имеет предел.
Очевидно, что
,
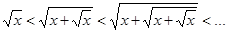т. е. последовательность 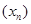возрастает. Далее находим
.
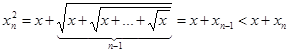Из неравенства
,
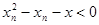учитывая, что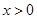 
и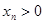 
, получаем
,
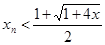т. е. последовательность 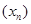ограничена.
Таким образом, доказано, что последовательность 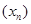сходится. Воспользуемся еще раз равенством:
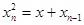. (2)
Если 
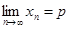, то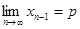 
. Переходя к пределу в равенстве (2), получим:
.
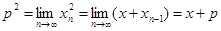Отсюда
.
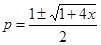Так как предел возрастающей последовательности с положительными членами не может быть отрицательным числом, то
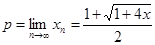. (3)
Пользуясь (3), уравнение (1) перепишем в виде
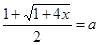
и находим единственное решение уравнения (1):
,
.
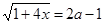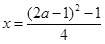Теперь покажем, что последовательность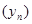 
, где
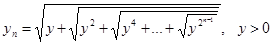(4)
сходится, и вычислим ее предел.
Равенство (4) запишем так:
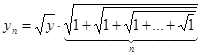. (5)
В силу (3), имеем
.
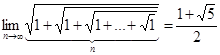Учитывая это равенство в (5), получим:
.
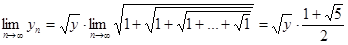Рассмотрим следующий пример.
Пример. Какое из чисел больше:
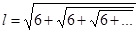
или
?
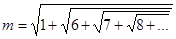Решение. На первый взгляд кажется, что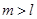 
, так как для образования числа 
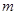берутся все числа натурального ряда больше 5 и единица, а для образования числа 
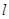используется только число 6. Однако если вычислить 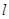по формуле (3) при 
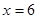получим:
.
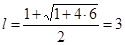Число 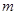оценим следующим образом:
.
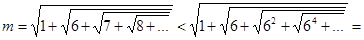
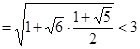Таким образом,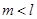 
.
Пример. Построить график функции:
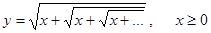. (6)
Решение. Легко видеть, что при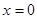 
, то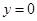 
. Если же 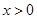, то по формуле (3) имеем:
.
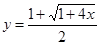Из этой формулы получим, что при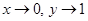 
.
Функция, заданная по формуле (6), получена с помощью арифметических операций над аргументом, извлечения корня и перехода к пределу. Однако эта функция разрывна в начале координат.
Выше мы рассматривали примеры на применение теоремы о пределе монотонной и ограниченной последовательности, отправляясь от функции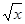 
. Понятно, что все рассмотренные результаты легко переносятся и на случай, когда исходной будет функция 
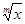при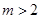 
.
Рассмотрим интересный пример, при решении которой не будем пользоваться формулой (3). При решении этого примера постараемся показать гармонию чисел и форм, геометрическое изящество математических объектов. А.Пуанкаре отмечал, что «всем истинным математикам знакомо настоящее эстетическое чувство» [1, стр.67]. В качестве задачи, иллюстрирующей эти положения рассмотрим следующий
Пример. Проверить истинность неравенства:
.
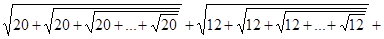
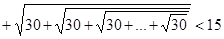Решение. Посмотрим, что произойдет с неравенством при изменении данных, а именно, если мы прибавим 5 к последнему числу в первом слагаемом (к 20), 4 к последнему числу во втором слагаемом (к 12) и 6 к последнему числу в третьем слагаемом (к 30). Тогда, после извлечения всех корней, получиться 5+4+6=15. Следовательно, без добавочного увеличения левая часть данного выражения действительно меньше 15.
Самостоятельное решение школьниками таких задач ведет к возникновению эмоционального удовлетворения. Это удовлетворение тем сильнее, чем больше усилий было затрачено на поиск решения. «Тот, кто хоть раз изведал благородную радость творческого достижения, никогда уже не пожалеет усилий, чтобы вновь ее испытать» [2, стр.153]. Стремление вновь испытать «радость творческого достижения» приводит к выработке совершенно особого отношения к творческим неудачам: ошибки не воспринимаются как поражение, а являются своеобразным «источником напряженной мысли и воли» [2, стр.153].
Литература:
1. Гнеденко Б. В. Формирование мировоззрения учащихся в процессе обучения математике. М.: Просвещение, 1982, 144 с.
2. Хинчин А. Я. Педагогические статьи /А. Я. Хинчин/ Под ред. Б. В. Гнеденко. М.: Изд-во АПН РСФСР, 1963, 204 с.
