Рассмотрено поведение квантовых двухуровневых систем, перспективных для использования в качестве ячеек памяти (кубитов) в квантовых компьютерах и системах квантовой коммуникации. Исследованы механизмы затухания фазовой информации, обрабатываемой импульсами СВЧ поля в квантовых устройствах (квантовых компьютерах). Показано, что эффективным механизмом является радиационный механизм, связанный с потерями в резонаторе.
Ключевые слова: спин, кубит, нутации, радиационное затухание.
Современные цифровые устройства передачи, приема и обработки информации (например, компьютеры) оперируют с классической двухуровневой системой; при этом система находится в одном из двух возможных состояний (например, заряд есть или заряда нет; напряжение есть или его нет; состояние системы намагниченное или размагниченное; состояние 0 или состояние 1 и т. д.). Объекты с двумя такими состояниями получили название «бит». В отличие от такой классической системы, квантовая двухуровневая система может находиться в произвольном состоянии, являющемся суперпозицией квантовых состояний 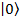 и
и 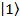 :
: 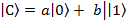 , где |a|2 + |b|2 = 1. Примерами таких двухуровневых систем являются спины парамагнитных атомов и ионов (например, электронный спин примесного иона фосфора Р в кремнии), спиновые состояния различных точечных дефектов в кристаллах (например, центры вакансии азота в алмазе, Е' – центры в кварце и т.д.). Квантовые двухуровневые системы называются кубитами. Предполагается, что такие кубиты могут служить рабочим элементом будущих квантовых устройств обработки информации (в частности, квантовых компьютеров). Благодаря свойствам квантовой суперпозиции и квантовой перепутанности (entanglement), квантовые компьютеры окажутся намного эффективнее (быстродействующие), чем современные классические компьютеры.
, где |a|2 + |b|2 = 1. Примерами таких двухуровневых систем являются спины парамагнитных атомов и ионов (например, электронный спин примесного иона фосфора Р в кремнии), спиновые состояния различных точечных дефектов в кристаллах (например, центры вакансии азота в алмазе, Е' – центры в кварце и т.д.). Квантовые двухуровневые системы называются кубитами. Предполагается, что такие кубиты могут служить рабочим элементом будущих квантовых устройств обработки информации (в частности, квантовых компьютеров). Благодаря свойствам квантовой суперпозиции и квантовой перепутанности (entanglement), квантовые компьютеры окажутся намного эффективнее (быстродействующие), чем современные классические компьютеры.
Процесс квантовой обработки информации включает воздействие на систему кубитов импульсами резонансного электромагнитного (ЭМ) поля H(t) = H1cos(ω0t) различной длительности и интенсивности. Во время действия импульса происходят прецессия поперечных компонент спинов вокруг приложенного постоянного поля H0 и затухающие во времени колебания (осцилляции) их амплитуды, называемые нутациями (или осцилляциями Раби). Сообщенная системе когерентная информация уменьшается (теряется, релаксирует) с той или иной скоростью как во время действия импульса, так и после его окончания (или между импульсами в случае последовательности импульсов). Изучение природы и различных характеристик этой релаксации имеет первостепенное значение при выборе рабочего материала и условий работы квантового устройства.
Цель данной работы – теоретическое исследование природы и физических механизмов указанной релаксации во время нутаций. Работа квантового устройства предполагает помещение рабочего тела (чаще всего – кусочка парамагнитного кристалла, содержащего указанные выше спины-кубиты) в резонатор, куда по волноводу подаются импульсы ЭМ-поля резонансной частоты, содержащие фазовую информацию. В процессе обработки этой информации кубиты поглощают кванты ЭМ-поля, совершают прецессионное движение и испускают поглощенные кванты поля, которые в свою очередь поглощаются стенками резонатора, что представляет собой обработанный сигнал информации, который принимается приемником. В этом процессе спины (элементарные магнитики электронов) взаимодействуют друг с другом, со спинами парамагнитных ядер, с колебаниями кристаллической решетки (с фононами) и со степенями свободы резонатора, в результате чего и происходит уменьшение полезной информации импульсов. При низких температурах потери из-за взаимодействия с фононами малы, поэтому основными источниками релаксации являются диполь-дипольные взаимодействия спинов друг с другом и так называемое радиационное затухание, обусловленное взаимодействием спинов со стенками резонатора (выделение тепла на стенках из-за их активного сопротивления токам, создаваемым прецессирующими спинами).
В работе детально исследованы механизмы указанных двух взаимодействий. Расчет сигнала нутаций производится путем решения квантовых уравнений движения спинов S = ½, то есть уравнений Гейзенберга, во вращающейся системе координат :
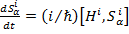 ; Hi =
; Hi = 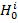 +
+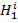 +
+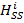 +
+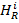 . (1)
. (1)
Здесь α = x, y, z, 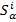 – α-компонента i-го спина, Hi – гамильтониан рассматриваемой задачи (во вращающейся системе координат, в которой Hi не зависит от времени), состоящий из гамильтонианов взаимодействия с постоянным и переменным магнитными полями, диполь-дипольного и радиационного взаимодействий, соответственно. Явные выражения первых трех слагаемых в Hi имеют общеизвестный стандартный вид и здесь не приводятся. Важным результатом данной работы является впервые полученный здесь гамильтониан радиационного взаимодействия (для i-го спина)
– α-компонента i-го спина, Hi – гамильтониан рассматриваемой задачи (во вращающейся системе координат, в которой Hi не зависит от времени), состоящий из гамильтонианов взаимодействия с постоянным и переменным магнитными полями, диполь-дипольного и радиационного взаимодействий, соответственно. Явные выражения первых трех слагаемых в Hi имеют общеизвестный стандартный вид и здесь не приводятся. Важным результатом данной работы является впервые полученный здесь гамильтониан радиационного взаимодействия (для i-го спина) 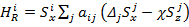 , где aij = a0/
, где aij = a0/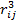 , rij – расстояние между i-ым и j-ым спинами, a0 – геометрический параметр, зависящий от формы и размеров резонатора и определяемый из сравнения теории с экспериментом; далее, Δj = ω0 – ωj – разность между частотой ЭМ-поля и резонансной частотой j-го спина, χ = γH1 – так называемая частота Раби (γ – гиромагнитное отношение). Как правило, в твердых парамагнетиках резонансные частоты спинов ωj распределены относительно средней частоты Ω по некоторому закону f(ω) = f(Δ), который обычно аппроксимируется гауссовским распределением «спиновых пакетов» (такой разброс резонансных частот носит название «неоднородное уширение резонансной линии»). При этом частоту поля ω0 подбирают равной Ω.
, rij – расстояние между i-ым и j-ым спинами, a0 – геометрический параметр, зависящий от формы и размеров резонатора и определяемый из сравнения теории с экспериментом; далее, Δj = ω0 – ωj – разность между частотой ЭМ-поля и резонансной частотой j-го спина, χ = γH1 – так называемая частота Раби (γ – гиромагнитное отношение). Как правило, в твердых парамагнетиках резонансные частоты спинов ωj распределены относительно средней частоты Ω по некоторому закону f(ω) = f(Δ), который обычно аппроксимируется гауссовским распределением «спиновых пакетов» (такой разброс резонансных частот носит название «неоднородное уширение резонансной линии»). При этом частоту поля ω0 подбирают равной Ω.
Решая уравнения (1) с гамильтонианом Hi, мы получаем 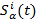 как явные функции времени. Далее, суммируя по всем спинам (фактически это означает интегрирование по указанному выше неоднородному распределению резонансных частот спинов), получаются усредненные по всей системе выражения для макроскопических компонент осциллирующей во времени намагниченности
как явные функции времени. Далее, суммируя по всем спинам (фактически это означает интегрирование по указанному выше неоднородному распределению резонансных частот спинов), получаются усредненные по всей системе выражения для макроскопических компонент осциллирующей во времени намагниченности 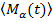 ~
~ 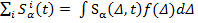 . Сигнал нутаций пропорционален y-компоненте намагниченности
. Сигнал нутаций пропорционален y-компоненте намагниченности 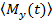 .
.
В работе получена общая формула для 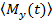 , которая учитывает вклад диполь-дипольного и радиационного взаимодействий одновременно и имеет вид:
, которая учитывает вклад диполь-дипольного и радиационного взаимодействий одновременно и имеет вид:
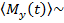
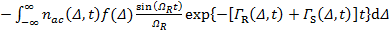 . (2)
. (2)
Здесь 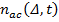 – спектральная плотность спинов, возбужденных в момент времени t действия импульса,
– спектральная плотность спинов, возбужденных в момент времени t действия импульса, 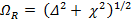 – обобщенная частота Раби. Величины
– обобщенная частота Раби. Величины 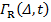 и
и 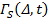 как раз дают интересующий нас вклад в экспоненциальное затухание сигнала от радиационного и диполь-дипольного взаимодействий, соответственно. К сожалению, они представляют собой несколько громоздкие формулы в виде интегралов и здесь не приводятся. Однако они легко исследуются численно, и в работе проведен полный анализ их свойств.
как раз дают интересующий нас вклад в экспоненциальное затухание сигнала от радиационного и диполь-дипольного взаимодействий, соответственно. К сожалению, они представляют собой несколько громоздкие формулы в виде интегралов и здесь не приводятся. Однако они легко исследуются численно, и в работе проведен полный анализ их свойств.
Предыдущие теории нутации исходили из так называемых уравнений Блоха с постоянными параметрами Γ = 1/T2 и T1 и что постоянная затухания Γ обусловлена взаимодействием диполей друг с другом. Однако в опытах Боскаино с сотрудниками [[1]] показано, что Γ не является постоянным параметром, а возрастает на порядок с ростом амплитуды ЭМ-поля H1 (то есть χ) по закону Γ = α + βχ, где α и β – параметры, различные для разных образцов. Кроме того, Γ возрастает с увеличением концентрации парамагнитных центров (спинов) n.
В данной работе показано, что дипольный вклад в релаксацию,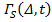 , пренебрежимо мал. Можно сказать, что хаотичные магнитные поля, создаваемые другими спинами на любом данном спине и создающие релаксацию сигнала, взаимно компенсируют друг друга, если парамагнитные центры по образцу распределены равномерно.
, пренебрежимо мал. Можно сказать, что хаотичные магнитные поля, создаваемые другими спинами на любом данном спине и создающие релаксацию сигнала, взаимно компенсируют друг друга, если парамагнитные центры по образцу распределены равномерно.
В то же время, вклад радиационного механизма в затухание, описываемый параметром 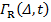 , оказывается в полном согласии с опытами [1]. Этот параметр, который правильнее писать как
, оказывается в полном согласии с опытами [1]. Этот параметр, который правильнее писать как 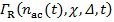 , представляет собой коэффициент затухания спинового пакета с разностной частотой Δ = ω0 – ω. Таким образом, в отличие от модели Блоха с постоянным для всего образца параметром Γ = 1/T2, каждый спин-пакет затухает со своим коэффициентом затухания, который зависит от амплитуды ЭМ-поля χ, от полной концентрации возбужденных спинов nac(t) и, конечно, от времени, так как концентрация возбужденных спинов возрастает во время действия импульса. Как видно из формулы (2), суммарный отклик всего образца есть интегральная сумма откликов всех спиновых пакетов, которые релаксируют описанным только что образом. Из численного анализа этого выражения следует, что затухание суммарного отклика дается вышеприведенной формулой Γ(n, χ) = α + β(n)χ, как это видно из рисунка 1 затухающих нутационных колебаний и из рисунка 2 зависимости Γ(n, χ) от χ для трех образцов с концентрациями n1< n2<n3.
, представляет собой коэффициент затухания спинового пакета с разностной частотой Δ = ω0 – ω. Таким образом, в отличие от модели Блоха с постоянным для всего образца параметром Γ = 1/T2, каждый спин-пакет затухает со своим коэффициентом затухания, который зависит от амплитуды ЭМ-поля χ, от полной концентрации возбужденных спинов nac(t) и, конечно, от времени, так как концентрация возбужденных спинов возрастает во время действия импульса. Как видно из формулы (2), суммарный отклик всего образца есть интегральная сумма откликов всех спиновых пакетов, которые релаксируют описанным только что образом. Из численного анализа этого выражения следует, что затухание суммарного отклика дается вышеприведенной формулой Γ(n, χ) = α + β(n)χ, как это видно из рисунка 1 затухающих нутационных колебаний и из рисунка 2 зависимости Γ(n, χ) от χ для трех образцов с концентрациями n1< n2<n3.
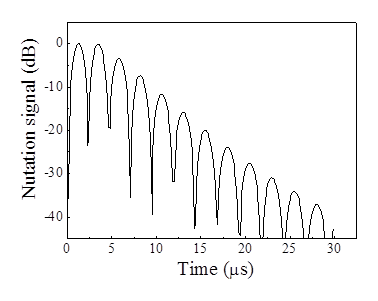
Рис. 1. Сигнал затухающих нутаций.
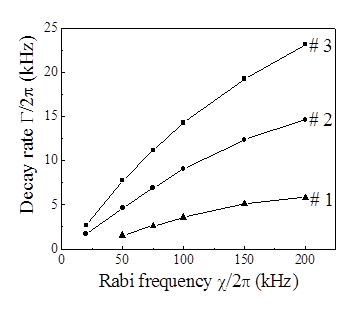
Рис.2. Коэффициент затухания Γ для трех образцов с концентрациями n1< n2<n3
Литература:
1. Boscaino R. et al. 1993 Phys. Rev.B 48, 7077; Agnello S. et al. 1999 Phys. Rev.A 59, 4087







