Рассмотрена возможность применения компьютерных моделей системы Wolfram Mathematica для демонстрации законов квантовой механики.
Ключевые слова: квантовая механика, интерактивная демонстрация, компьютерная модель.
Квантовая механика — один из самых сложных разделов в лекционном курсе общей физики. Для его понимания нужны хорошие знания не только физики, но и высшей математики, например, надо знать теорию решения дифференциальных уравнений. К сожалению, количество часов, отведенных на лекции по физике, уменьшается, а знания студентов не становятся лучше. Наглядная демонстрация решения простейших задач квантовой механики значительно улучшает понимание ее законов. В сети Интернет существует большое количество различных материалов, созданных с помощью разнообразных программных продуктов. Их создание требует специальных знаний в области программирования, разработки достаточно сложны и недешевы. Например, многие интерактивные моделирующие программы используют технологии Java [1]. Часто используются также Flash-технологии [2]. Разработки компании Wolfram Research созданы на основе CDF-технологии (Computable Document Format) с помощью системы Wolfram Mathematica. Сайт компании имеет раздел «Demonstration project», материалы этого раздела находятся в открытом доступе.
Система Wolfram Mathematica — это постоянно совершенствующаяся система, фактически ставшая самой мощной вычислительной системой мира. С помощью этой системы можно создавать интерактивные лекции-презентации, используя уже имеющиеся компьютерные модели или создавая свои.
Покажем, как продемонстрировать решение простейших одномерных задач квантовой механики с помощью таких интерактивных моделей.
На рис.1а и 2б изображены волновые функции частицы в одномерной прямоугольной потенциальной яме. Интерактивная анимация позволяет изменять ширину и глубину ямы, при этом меняется вид волновых функций и расстояние между энергетическими уровнями. Видно, что энергия частицы может принимать только определенные дискретные значения, то есть находиться только на определенных уровнях энергии.
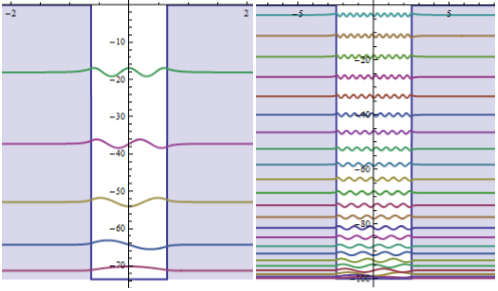
Рис.1. а, б
Если размеры ямы малы (рис.1а), то уровни энергии заметно дискретны. Если же размеры ямы увеличить (рис.1б), то расстояние между уровнями сильно уменьшается и при очень широкой яме энергетический спектр становится непрерывным. На этом примере хорошо виден переход от законов квантовой механики к классической физике.
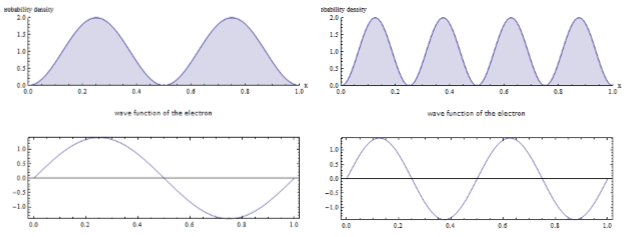
Рис. 2. а, б
Более подробно волновые функции и плотность вероятности обнаружения частицы на различных расстояниях от стенок ямы можно показать на примере следующей демонстрации. Анимированные графики позволяют менять главное квантовое число n от 1 до 10, показывая, как при этом меняется вид волновой функции. На рис.2 приведены волновые функции ψn (x) (нижние кривые) и плотностивероятности │ψn (x)│2 (верхние кривые) для n=2 (рис.2а) и n=4 (рис.2б). При n=2 частица не может находиться в середине ямы, а с одинаковой вероятностью может находиться в ее левой и правой части. При n=3 вероятность также в разных местах ямы различна.. Модель показывает, что в квантовой механике нельзя говорить о траектории частицы.
Еще один характерный пример — прохождение частицы через потенциальный барьер (туннельный эффект). Компьютерная модель позволяет менять ширину и высоту барьера, и энергию частицы. На рис.3а изображен широкий потенциальный барьер. Энергия частицы меньше высоты барьера (штриховые линии). Нижний рисунок — волновые функции частицы (действительная и мнимая части). Это классический случай — частица отражается от такого барьера. Рис3б. — узкий барьер, энергия частицы меньше высоты барьера. В этом случае наблюдается туннельный эффект- проникновение частицы за барьер. Наконец, рис.3в. показывает, что даже если энергия частицы больше высоты барьера, частица может и отразиться от него, что в классической механике невозможно.
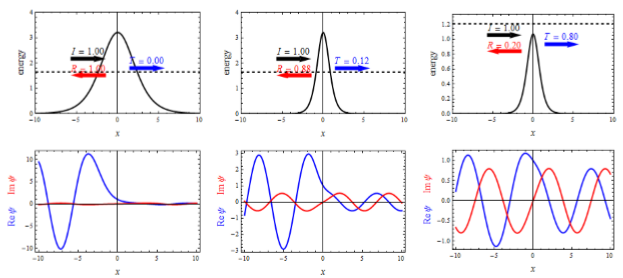
Рис.3. а, б, в
Раздел «Demonstration project» содержит большое количество примеров решения различных задач квантовой механики средствами Wolfram Mathematica. Содержание каждой демонстрации проверено экспертами компании. Компьютерная анимация сопровождается пояснительным текстом и необходимыми формулами.
Применение компьютерных анимационных моделей и графиков сокращает время изложения сложных разделов квантовой механики и улучшает их понимание, что повышает эффективность усвоения лекционного материала.
Литература:
1. Постникова Е. И., В. В. Ларионов. Лекционные занятия по физике в условиях информатизации образования в ВУЗе // Изв.Томского политехнического университета. 2007, т.310, № 2. — С.249–253.
2. Бутиков Е. И. Компьютерные модели для изучения динамики твердого тела // XIII Всероссийская научно-методическая конференция «Телематика'2006», Санкт-Петербург, 5–8 июня 2006 г. С. 350–351.







