Теоретически исследовано явление осцилляции магнитного потока в результате термомагнитной неустойчивости критического состояния в сверхпроводнике. Изучены пространственные и временные распределения тепловых и электромагнитных возмущений в плоском полубесконечном сверхпроводящем образце в режиме вязкого течения потока с линейной вольт-амперной характеристикой.
Ключевые слова: вихри, колебание, критическое состояние.
The phenomenon of an ostsillyation of a magnetic flux as a result of thermomagnetic instability of critical condition in a superconductor is theoretically investigated. Spatial and temporary distributions of thermal and electromagnetic indignations in a flat semi-infinite superconducting sample in the mode of a viscous current of a stream with the straight-line volt-ampere characteristic are studied.
Keywords: whirlwinds, fluctuation, critical condition.
Динамика устойчивости критического состояния по отношению к скачкам магнитного потока в жестких и композитных сверхпроводниках была обсуждена в теоретических и экспериментальных работах [1–5]. Общая концепция устойчивости критического состояния в сверхпроводниках — II рода была развита в литературе [4, 5]. В работе [5] изучена динамика развития малых тепловых и электромагнитных возмущений и соответствующие условия устойчивости критического состояния в сверхпроводниках в режиме вязкого течения потока. В последнее время огромное внимание уделяется к явлению осцилляции магнитного потока, возникающие в результате термомагнитной неустойчивости в сверхпроводниках [6]. В процессе исследования динамики термомагнитных неустойчивостей обнаружены колебательные моды в смешанном состоянии сверхпроводящего Nb-Ti образца, как результат катастрофической лавины [7]. Для объяснения наблюдаемых осцилляционных процессов была предложена теоретическая модель, которая учитывает инерционные свойства вихревой материи [8]. В работе [9] были изучены динамические свойства вихревой материи в Nb-Ti сверхпроводнике. Осцилляционные явления были интерпретированы как результат существования конечной величины эффективной массы вихря, т. е. колебания могут рассматриваться как проявление инерционных свойств вихревой материи [10]. В данной работе теоретически исследовано явление осцилляции магнитного потока в результате термомагнитной неустойчивости критического состояния в сверхпроводнике.
Для моделирования процесса эволюции возмущений температуры и электромагнитного поля используется система уравнений макроскопической электродинамики. Распределение магнитной индукции 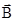 (r, t) и транспортного тока
(r, t) и транспортного тока 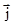 (r, t) в сверхпроводнике определяется уравнением
(r, t) в сверхпроводнике определяется уравнением
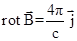 (1)
(1)
В режиме вязкого течения потока взаимосвязь между магнитной индукцией 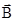 (r, t) и электрическим полем
(r, t) и электрическим полем 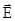 (r, t) устанавливается уравнениями Максвелла
(r, t) устанавливается уравнениями Максвелла
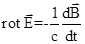 (2)
(2)
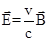 (3)
(3)
Уравнение движения вихрей можно написать в виде [6].
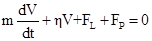 (4)
(4)
где m — масса вихря единичной длины, 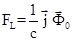 — сила Лоренца,
— сила Лоренца, 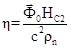 — коэффициент вязкости,
— коэффициент вязкости, 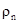 — сопротивление в нормальном состоянии,
— сопротивление в нормальном состоянии, 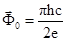 — квант магнитного потока,
— квант магнитного потока, 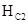 — верхнее критическое поле [1]. Соответственно, распределение температуры в образце определяется уравнением теплопроводности
— верхнее критическое поле [1]. Соответственно, распределение температуры в образце определяется уравнением теплопроводности
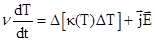 (5)
(5)
где 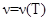 и
и 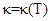 — коэффициенты теплоемкости и теплопроводности образца, соответственно.
— коэффициенты теплоемкости и теплопроводности образца, соответственно.
Воспользуемся моделью Бина для плотности тока и предположим, что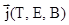 не зависит от индукции магнитного поля
не зависит от индукции магнитного поля 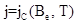 , i.e.,
, i.e., 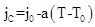 [1], где
[1], где 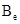 - значение внешней магнитной индукции;
- значение внешней магнитной индукции; 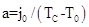 ;
; 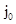 — равновесная плотность тока,
— равновесная плотность тока, 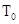 и
и 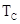 — начальная и критическая температура образца, соответственно [5].
— начальная и критическая температура образца, соответственно [5].
Сформулируем основные уравнения, описывающие динамику развития тепловых и электромагнитных возмущений для простого случая — сверхпроводящего плоского полубесконечного образца 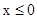 . Предполагаем, что внешнее магнитное поле
. Предполагаем, что внешнее магнитное поле 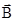 =(0, 0,
=(0, 0, 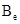 ) направлено по оси z и скорость магнитного поля является постоянной
) направлено по оси z и скорость магнитного поля является постоянной 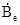 =const. Согласно уравнению Максвелла (2), в образце имеется вихревое электрическое поле
=const. Согласно уравнению Максвелла (2), в образце имеется вихревое электрическое поле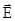 =(0,
=(0, 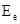 , 0). Здесь
, 0). Здесь 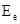 амплитуда фонового электрического поля. Будем искать решение системы уравнений (3)-(5) в виде
амплитуда фонового электрического поля. Будем искать решение системы уравнений (3)-(5) в виде
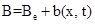
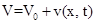 (6)
(6)
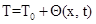
(где 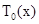 ,
, 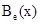 и
и 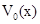 решение уравнения (1)-(5) полученные в квазистационарном приближении). Подставляя последнее в исходную систему, имеем следующие
решение уравнения (1)-(5) полученные в квазистационарном приближении). Подставляя последнее в исходную систему, имеем следующие
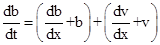 (7)
(7)
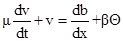 (8)
(8)
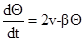 (9)
(9)
где были введены безразмерные параметры
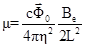 ,
, 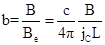 ,
, 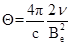 ,
, 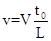 ,
, 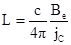 и переменные
и переменные 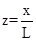 ,
, 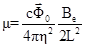
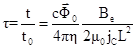 .
.
Здесь L глубина проникновения магнитного поля вглубь сверхпроводника [5]. Для малых тепловых и электромагнитных возмущений 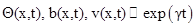 (где
(где 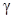 - собственное число задачи) нетрудно получить дисперсионное соотношение, определяющее собственное число задачи
- собственное число задачи) нетрудно получить дисперсионное соотношение, определяющее собственное число задачи
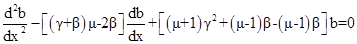 (10)
(10)
Неустойчивость магнитного фронта, как правило [5], определяется положительными значениями инкремента 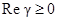 . Тогда можно предположить, что неустойчивость возникает при условии
. Тогда можно предположить, что неустойчивость возникает при условии 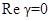 . Анализ дисперсионного соотношения показывает, что инкремент нарастания положителен
. Анализ дисперсионного соотношения показывает, что инкремент нарастания положителен 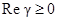 , если выполняется условиеf
, если выполняется условиеf 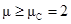 . В этом случае малые возмущения нарастает со временем (согласно (6)) и фронт магнитного потока неустойчив. В случае, когда
. В этом случае малые возмущения нарастает со временем (согласно (6)) и фронт магнитного потока неустойчив. В случае, когда 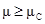 инкремент нарастания является отрицательным и любое малое возмущение будет затухать. При критическом значении
инкремент нарастания является отрицательным и любое малое возмущение будет затухать. При критическом значении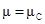 инкремент нарастания равен нулю
инкремент нарастания равен нулю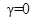 .
.
Заключение
В данной работе мы изучаем пространственное и временное развитие маленького теплового и магнитного волнения в образце сверхпроводника типа-II в режиме потока потока, предполагая, что прикладная полевая параллель на поверхность образца. На основе линейного анализа ряда отличительных уравнений, описывающих маленькие волнения температурного и магнитного поля, мы будем найденный, который под некоторой нестабильностью условий может произойти в образце, который принимает во внимание инерционные свойства массы вихрей.
Литература:
1. C. P. Bean, Phys. Rev. Lett., 8, 250, 1962; Rev. Mod. Phys., 36, 31, 1964.
2. P. S. Swartz and S. P. Bean, J. Appl. Phys., 39, 4991, 1968.
3. S. L. Wipf, Cryogenics, 31, 936, 1961.
4. R. G. Mints, and A. L. Rakhmanov, Rev. Mod. Phys., 53, 551, 1981.
5. R. G. Mints and A. L. Rakhmanov, Instabilities in superconductors, Moscow, Nauka, 362, 1984.
6. V. V. Chabanenko, V. F. Rusakov, V. A. Yampol’skii, S. Piechota, A. Nabialek, S. V. Vasiliev, and H. Szymczak, arXiv: cond-mat/0106379v2, 2002.
7. S. Vasiliev, A. Nabialek, V. Chabanenko, V. Rusakov, S. Piechota, H. Szymczak, Acta Phys. Pol. A 109, 661, 2006.
8. Nabialek, S. Vasiliev, V. Chabanenko, V. Rusakov, S. Piechota, H. Szymczak, Acta Phys. Pol. A, 114, 2008.
9. S. Vasiliev, A. Nabialek, V. F. Rusakov, L. V. Belevtsov, V. V. Chabanenko and H. Szymczak, Acta Phys. Pol. A, 118, 2010.
10. V. Rusakov, S. Vasilieva, V. V. Chabanenko, A. Yurov, A.Nabialek, S. Piechotaa and H. Szymczak, Acta Phys. Pol. A, 109, 2006.







