В работе предложен новый подход к описанию и оптимизации интегрального критерия качества выбранных свойств системы методами нелинейного программирования, где в качестве параметризации выбираются стоимостные характеристики. Приведены примеры постановок задач и алгоритмы их решения для получения оптимальных по стоимости сухих строительных смесей, удовлетворяющих заданным техническим требованиям по их свойствам. Обоснованы критериальные соотношения для нахождения рациональных путей их улучшения.
Ключевые слова:шкалирование, интегральный критерий качества, стоимостная параметризация, минимизация, задача с ограничениями, рациональные пути.
In this paper we propose a new approach to the description and optimization of integrated quality criterion is selected, the system properties by methods of nonlinear programming, where the parameterization chosen cost characteristics. Examples of formulations of problems and algorithms for their solution to obtain the optimal cost of dry mixes that meet the specified technical requirements on their properties. Justified criterion relationships for the rational ways of their improvement.
Key words: scaling, the integral criterion of quality, cost parameterization, minimization, task constraints, rational way.
Одними из работоспособных инструментов оценки и управления качеством системы являются, как известно [1–3], интегральные (обобщенные) критерии качества. Факторизация свойств системы, оценка каждого из факторов в отдельности и их весовых вкладов в общий критерий позволяют оценить его общее значение, а также выделить основные факторы, влияющие на его возрастание (рост качества), а значит обосновать оптимальные пути приращения качества, т. е. возможность управления. Как правило, факторы в своем содержательном (физическом) смысле и размерностях между собой несравнимы, а аргументы, от которых они зависят, также изменяются в различных пределах. Задача количественного сравнения свойств решается известными методами шкалирования переменных [4]. Очевидно, что задача сопоставления уровня влияния каждого из факторов на результирующее значение интегрального критерия и путей повышения его значения каждый раз сводится к выбору общих характерных параметров меры влияния частных факторов на весь критерий. Выбор таких параметров определяется содержательной стороной решаемой проблемы.
Для многих задач оптимизации и в первую очередь касающихся хозяйственной деятельности, таким параметром, служит стоимость. В настоящей работе предложен один из возможных подходов к оптимизации интегрального критерия качества путем параметризации всех частичных факторов через стоимостные характеристики. Если под оптимальным понимать критерий оптимальности
: 
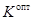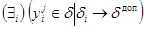
а правилом, согласно которому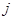 
— я система считается оптимальной по 
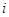— у показателю качества следующим: существует, хотя бы один частный показатель 
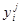, значение которого принадлежит области адекватности, а радиус этой области по этому показателю оптимален. Выбирая в качестве общего размерного аргумента стоимость, а в качестве 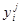нужные для данной задачи показатели, будем искать максимум значения интегрального критерия при минимальных затратах. Для этого необходимо построить математическую модель решаемой задачи, в качестве целевой функции обосновать вид интегрального критерия и каждого из факторов, привести их к безразмерной форме, сформулировать ограничения на переменные и найти решение полученной оптимизационной задачи либо известными методами, либо развить методы, учитывая специфику содержательной задачи.
Заметим, что наряду с нахождением оптимального значения стоимости и качественного состояния системы такой системы, можно ставить задачи выбора рациональных путей повышения уровня качества, влиянием на выбранный фактор или группу факторов по заданной стоимости, например, решать задачу управления качеством с минимизацией затрат.
Покажем это на примере интегрального критерия в виде линейной свертки
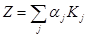
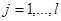(1)
естественного условия нормирования: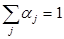 
, 
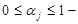весовые множители Kj≥ 0 — частные критерии свойств системы для одной из одной из оптимизационных задач создания строительных материалов.
Задача 1.
Найти состав компонентов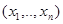 
с заданными удельными стоимостями 
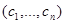, обеспечивающий максимальное значение интегрального критерия Z при минимальной удельной стоимости общего состава смеси 
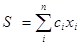и заданных ограничениях.
, 
, 
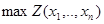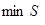
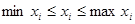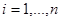(2)
,
, 
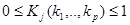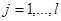
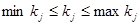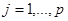
Ограничения определяются нормативными документами, экспертными оценками, приобретённым опытом и др. При такой параметризации все функции многих переменных, зависящие от составов, становятся функциями от одной. стоимостной переменной S, а выражение (1) можно рассматривать, как стоимостной интегральный критерий качества.
Задача 2.
Обосновать принятие решений по вложению затрат заданного уровня в приращение значения определенного частного критерия или группы критериев качества для повышения общего качества системы.
Рассмотрим выражение полного дифференциала интегрального критерия в некоторой выбранной точке.
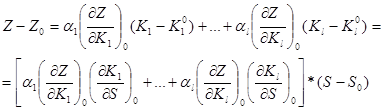(3)
где нулевым индексом и без него обозначены значения параметров в зафиксированной нулевой и произвольной точках. Кj — шкалированные коэффициенты j-го свойства материала, зависящие от частных критериев качества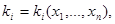 
, 
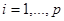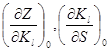- соответствующие частные производные от свойств и стоимости.
Шкалирование производится либо из экспериментальных данных по стандартным методикам (что предпочтительнее, но не всегда возможно) [4], либо с использованием экспертных оценок и функции Харрингтона (как правило, ввиду отсутствия более обоснованных данных) [5]. Численное значение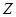
характеризует состояние системы, а его выражение (3) позволяет анализировать влияние каждого из факторов на изменение критерия качества при изменении удельной стоимости частного фактора на величину удельной стоимости S-S0и оценивать его стоимостной вклад в общее значение критерия при условии роста Условие роста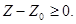 
В линейном приближении, из полного приращения для выбранной стадии состояния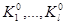
согласно (3)
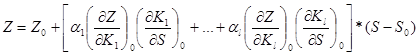(4)
Таким образом, переход системы из одной стадии состояния с независимыми частными характеристиками 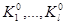в другое, с характеристиками 
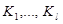, можно проанализировать, как изменение общего критерия 
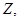так и изменение вкладов каждого из частных факторов.
Для прогноза изменения стадии состояния системы рассмотрим влияние каждого из частных факторов на ее поведение. При этом частные приращения шкалированных единиц, легко приводимых к реальным размерным физическим единицам через обратные взаимно-однозначные преобразования, характеризуют уровень необходимых финансовых затрат для перевода системы в качественно лучшее состояние. Сравнительным анализом приращений частных факторов и или группы факторов можно выбрать больший рост общего критерия с меньшими затратами, что позволяет управлять процессом выбора рациональных путей повышения качества системы.
Алгоритм такого выбора включает следующие основные стадии:
1. Определение частных производной от интегрального критерия и составляющих от полученной эмпирической (МНК) зависимости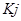 
или функции Харрингтона от состава и удельной стоимости S.
2. Выбор вектора желательного изменения признака 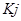для текущего состояния интегрального критерия 
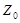в состояние .
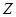3. Определение затрат на перевод системы в очередное состояние качества с использованием значений стоимости для таких изменений.
Практическое применение указанного алгоритма позволяет оценить общее состояние системы, находящейся под управляемым воздействием, обосновать способ улучшения и выбрать рациональные пути перевода её в более качественное состояние.
Эффективность применения такого подхода будет зависеть от обоснованности выбранного интегрального критерия качества и методов численного решения оптимизационной задачи (1)-(2).
Заметим, что если удается связать свойства системы и её качества непосредственно со стоимостью, то алгоритм нахождения максимума критерия формализуется вместе с анализом частных производных, например для вышеупомянутых задач строительства, из (3) несложно получить:
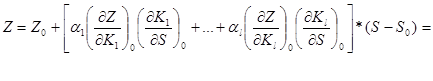
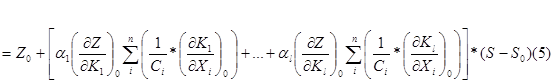
Отсюда видно, что каждый из членов несёт содержательный смысл при переходе в очередное состояние системы на единицу удельной стоимости и может быть проанализирован с рекомендациями для содержательного решения поставленной задачи.
Пример практической реализации данного подхода в виде задачи 1, подробно рассмотрен авторами [6,7], а в виде задачи 2 реализован также на задачах, связанных с выбором рациональных путей восстановления территорий, нарушенных строительством [8,9].
Литература:
1. Институт экономики и управления Киевского славистического университета. [Электронный ресурс] URL: http://elenagavrile.narod.ru/TPR/Lekcciya_25.pdf (Дата обращения: 30.02.2015).
2. Трошин А. Г., Камбург В. Г. Оценка и прогноз для управления процессом центробежного отжима зернистых материалов по уровню содержания пленочной влаги. Региональная архитектура и строительство. 2014. № 1. С. 150–155.
3. Камбург В. Г., Питак И. В., Моисеев В. Ф., Питак О. Я. Управление инвестиционно-строительным проектированием в жилищной сфере. Региональная архитектура и строительство. 2012. № 2. С. 181–187.
4. Ахназарова С. Л., Кафаров В. В. Методы оптимизации эксперимента в химической технологии. Издание 2-е изд., доп. и перераб. М.: ВШ.1985, 166 с.
5. Бубнов Е. А., Скороходов Д. А., Шкалирование входной информации в корабельных системах информационной поддержки. Вахтенный журнал, издательство «Гринда», № 12 2007
6. V. I. Loganina, V. G. Kamburg, L. V. Makarova, N. Y. Bodazhkov // Method of building optimization of composites based on the criterion analysis // journal of innovative technology and education Vol. 7, no. 28, HIKARI Ltd, Bulgaria 2014. St 1555–1563.
7. Камбург В. Г., Логанина В. И., Бодажков Н. Ю., Макарова Л. В. Оптимизация состава сухих строительных смесей с учетом их стоимости // Известия вузов. Строительство: Научно- теоретический журнал. — Новосибирск. 2014. № 6. С. 44–50.
8. Tupitsyna O., Kamburg V., Bodazhkov N., Bykov D. Criteria management of a choice of effective ways of a recreation of the territories broken by technogenic influence. interdisciplinary integration of science in technology, education and economy, Poland, 2013. 637–645
9. Тупицина О. В., Камбург В.Г, Чертес К. Л., Быков Д. Е. Критериальная оценка состояния нарушенных геосистем.// Нефтегазовое дело № 4 2012. с.231–241.
